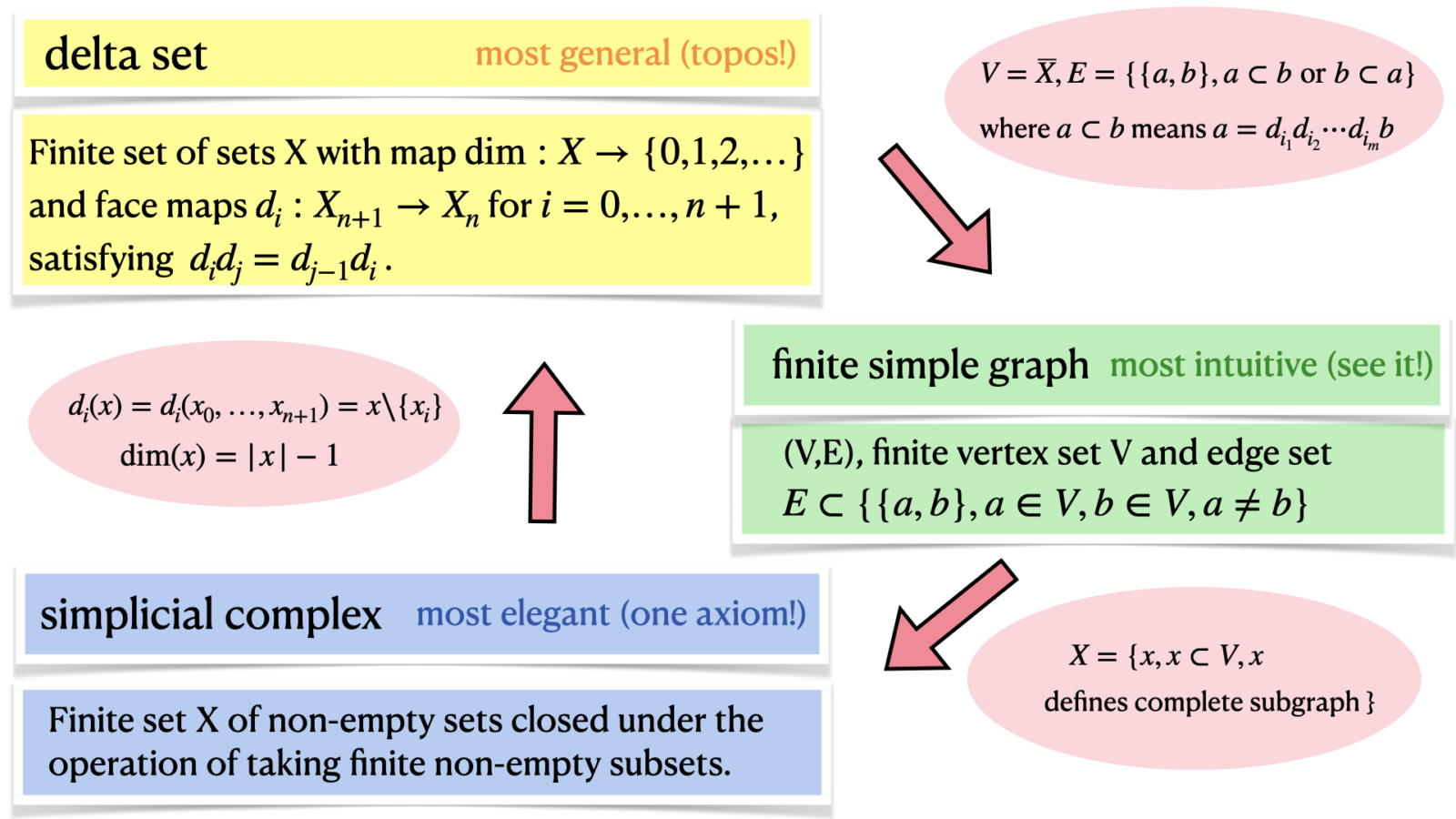
There are lots of finite geometric structures. Graphs are probably the most clear ones. Simplicial complexes can not be beaten in simplicity. And delta sets can not be surpassed by generality. So, they are a geometric incarnation of the paradigm “Simplicity, Clarity and Generality”, which appeared on the book cover of the cult book “The practice of Programming” by Brian Kernighan and Rob Pike
Maybe I add a personal remarks about unix. I got acquainted to UNIX, when ETHZ got Bernina (A VAX 11/785 which costed 400000 dollars at that time) in 1984. I got access to it shortly after and immediately fell in love with the paradigms of UNIX. It not only changed my view about computing but about organizing information in general. My files kept on computers has grown since 1984, where I had a couple of KBytes, to now maybe 10 Terabytes. Somehow, I keep my brain organized like a unix tree. Rather than keeping things all messed up in a “Documents” directory (as still many do today, working therefore very ineffectively), it is organized in a large tree, there are branches like programming, branches like Movies, branches like books, a tree of math. Thinking abilities are mostly just the ability to organize information effectively.
About the use of delta sets, a maybe more abstract category as it is a fancy topos. It is however very much down to earth and does not need much more than what is anyway done when implementing a geometric structure: we look at the simplicial complex of the graph for example, we form a list of the complete subgraphs and produce so a simplicial complex. This then automatically gives face maps and so exterior derivatives which can be conveniently encoded in a single matrix, the Dirac operator. When we deal with delta sets, we do not have the face maps yet in general. They have to be imposed additionally and the Dirac matrix is a good way to do so. Additionally, there are also shifts of dimensions which can not be read off directly. What can happen in the delta set case like for example when looking at open sets is that some of the blocks of the Hodge operator are 0x0 matrices.
Here is the poster.