Lagrange Riddle

In the program to get rid of any notion of infinity, one necessarily has to demonstrate that very classical and entrenched notions like topics appearing in a contemporary multi-variable calculus course can be replaced and used. Artificial discretisations do not help much in that; they serve as numerical schemes but not replacements for fundamental mathematical structures. Geometry and calculus in particular are great play-fields for that.

What is geometry? Archimedes would consider it a theory allowing to do measurements, like area or volume. After all, geometry means “measuring the world”. Euclid would probably have defined it as a theory dealing with geometric objects like points, lines, circles, length, angles and finding definitions, axioms, and theorems describing these objects. Klein consider it a theory of “symmetries”, where different geometries are characterized by their symmetry group. The symmetry group defines what type of geometry we have. Topology for example is characterized by the group of homeomorphisms. Klein’s program was already a move from the “objects” to the “morphisms”. Category theory later would strengthen this point of view. It became a central theme in the thinking of Grothendieck: shift to the morphisms, not the objects and one level higher, shift to functors rather than categories.

Claiming that everything is geometry but this is silly because it takes all meaning of the notion. Maybe, a good definition is to think of geometry as a theory which allows for a decent cohomology which relates to geometric properties. This in particular means that one has notions of dimension, Euler characteristic and connectivity properties of all kind dimensions. But it should not only be that. There should also be notions of derivatives or curvature which add up. There should be a Stokes and Gauss-Bonnet result for example. A bit surprising is that Stokes and Gauss are almost a joke in the discrete. Also the Lefshetz (and especially Brouwer) fixed point theorem is faster in the discrete. If you ask me even much more elegant as when you look at say the Lefshetz fixed point theorem in the continuum, we need to make technical assumptions like that the map has only finitely many fixed points. That is not guaranteed even in the category. One difficulty with these translations is then to realize and appreciate afterwards that these notions are related to the corresponding classical notions. The Mickey-Mouse mathematics actually is more appealing the grown-up math in some sense because it looks as if the finite formulations do the same, just without the technical overhead. To appreciate the discrete Gauss-Bonnet result for example, one has to see it using integral geometric notions. When doing so and see Euler curvature as an expectation of Poincare-Hopf indices one can directly relate it with Gauss-Bonnet-Chern in the continuum, where curvature is also an expectation of Poincare-Hopf indices of a suitable probability space of Morse functions ( obtained by Nash embedding the manifold into an ambient Euclidean space). A bit surprising, it was harder to get a good notion of hyper surface in a manifold. I got this only in 2015. And only now in 2023 know how to define the analog of discrete algebraic varieties without having to do ridiculous Barycenbtric refinements. The seemingly simplest things are sometimes the hardest and can produced puzzles which surprise. I still do not know how to formulate Lagrange multipliers in the discrete in a way that it can compete with the continuum. This talk today was a bit of an attempt to collect my thoughts about it. One snag in that was the realization that complex level surfaces $latex\{ \psi=0 \}$ and are not the same (which I actually find exciting) but this comes later in the talk.

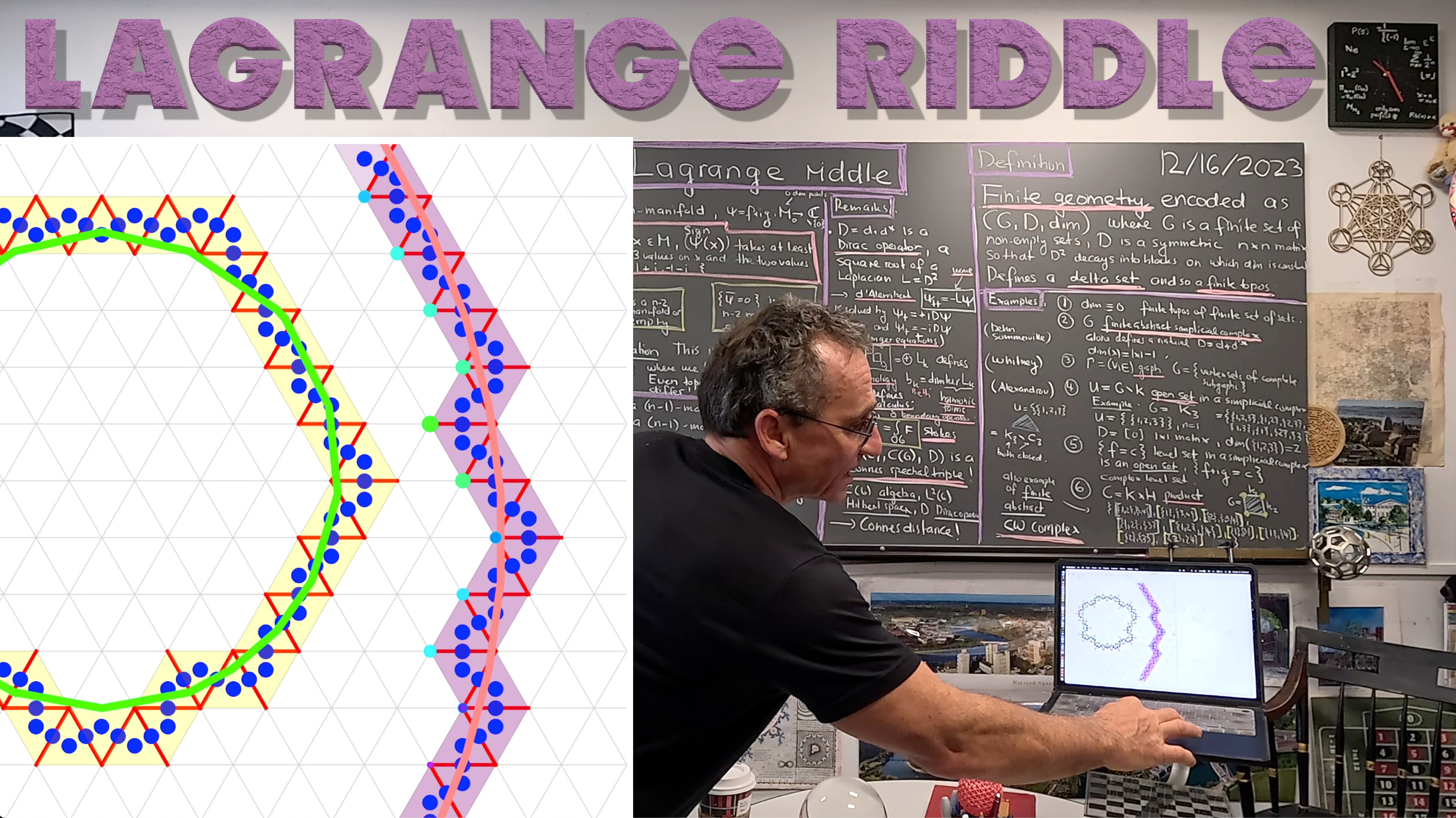
About the talk. I start a bit again with talking about the structure in which we work. It is based on set theory. This is maybe obvious because Cantor produced a paradise of sets “from which we can not be displaced” (Hilbert in a lecture given in Muenster 1925) and Hilbert was right. Indeed, also with the rise of alternative foundations like category theory, the actual implementation of mathematical structures can always be based on sets, similarly as the memory of any computer is just a single finite array of bits (the structure of the memory which one only appreciates if one works directly in the memory array as in the C programming language. I love-hate this pointer stuff. Love it because it is so fast, hate it because a tiny mistake can produce serious mistakes). Also the rise of other foundations like ETCS still is based on sets, or better Set, the category of sets, a topos. When removing infinity, one has to deal with FinSet, a finite topos which also exists if we refute infinity. But this is not yet geometry. The only counting we can do in FinSet is “count”. The only continuity property is “completely disconnected”. Really good geometry, one can start to do with delta sets, a notion more general and more intuitive than the special case of simplicial sets, the usual darling in that area. It needs specialists to explain just what the later is. This is not so much necessary for delta sets. It is just a set of sets on which additionally one has a Dirac operator. Of course, a set of sets also qualifies, just that we are then in a rather boring zero dimensional situation. Zero dimensional geometry is rather boring. Interesting structure comes in when assigning dimensions to each set and describe inclusion relations (face maps). A Dirac operator D is all we need also just for cohomology thanks to Hodge (and Eckmann who realized that this all works very well in finite structures). This fits me very well because I think like a computer scientist. I need to see things. If I talk about a structure, I need to be able to work with it which means, I need to be able to realize it.

So, how to deal with classical topics like Lagrange multipliers in the discrete like in a finite simple graph? The good news are we have good notion of level surface{ f=c} on a manifold. It is again a manifold (or empty) for all functions not taking values taken on the vertices. This fact can not be under estimated. It is absolutely crucial in geometry that we can talk about thinks like graphs of functions, that we have notions like the product of manifold structures and get manifolds. Almost all school mathematics relies on manifolds like the plane or three dimensional space. The situation is actually better even in the discrete. Now new is this works also with several functions. The surprise is that with this definition, {f=0,g=0} is not the same than {f=0, -g=0}. This looks a bit crazy but it is related to the definition made to define {f=0,g=0}. It took 8 years since 2015 to consider this. We require for a simplex to qualify to be on the level surface {f+ig=0} if the complex-valued function sign(f+ig) takes on values 1-i, 1+i and a third value different from those. This is an open set in the Alexandrov topology but is again a graph if we take the sets as vertices and connect two if one is contained in the other. If the host graph was a manifold, this is then a co-dimension 2 manifold. It is a different manifold than {f-ig=0} in general. Here is an example. (I think being able to produce random (n-2)- dimensional manifolds in a n dimensional host manifold is already a killer- app of this Sard theme .Lets pick as the host graph the 4-manifold , the 4 dimensional projective space. This is a simplicial complex with a vertex set of 16 points!) We like to take a non-orientable manifold because now, level surfaces can be non-orientable. Here is an example: we took two random functions f,g and got as a 2-torus and $latex \{ \overline{\psi}=0\} as a 2-sphere. It is a really nice and quick way to generate random 2 dimensional surfaces. One can get higher genus non-orientable surfaces easily like that like Klein bottles with many handles. Of course, this is not restricted to 2 manifolds. In principle we could generate random 11 dimensional manifolds in a 13 dimensional host graph. And the codimension 2 is also only a special case. The Sard theorem tells that in a n-dimensional manifold, we can get by picking k random functions get random n-k dimensional manifolds. A rich source of toys for kids like me who like to play.