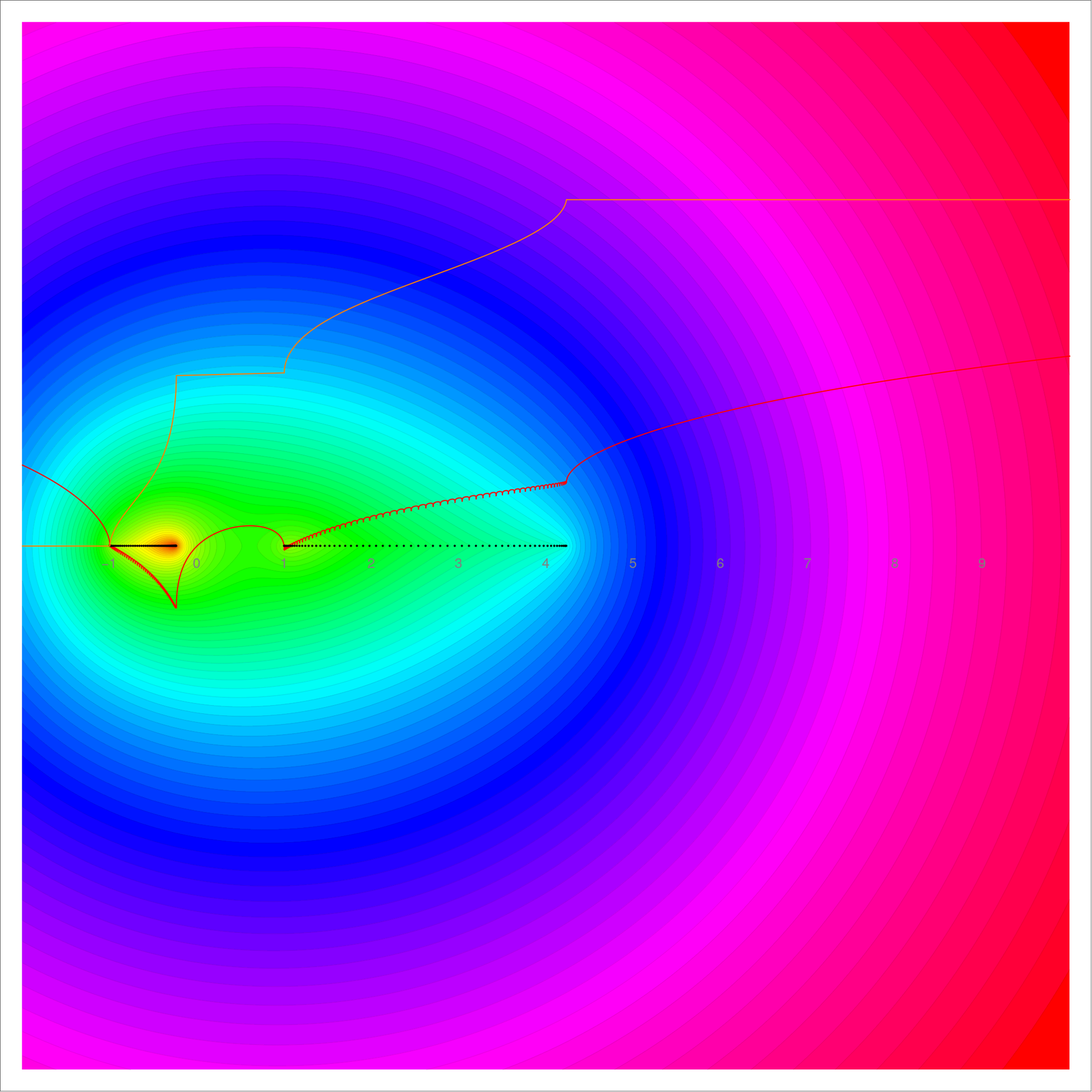
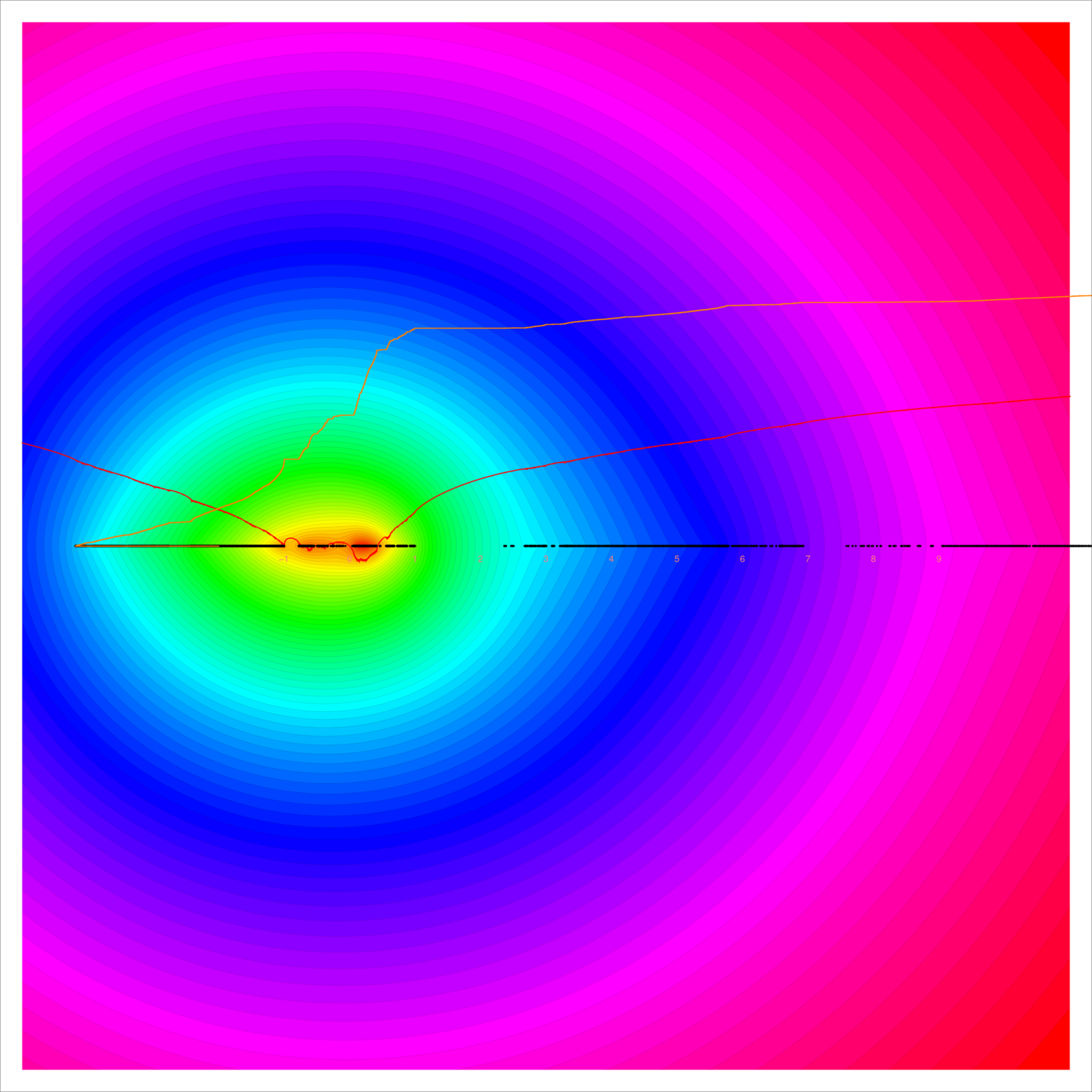
I explain a bit more why for graphs containing a d dimensional simplex, there are Barycentric refinements for which the arboricity is at least c(d), where c(d) can be obtained from the Perron-Frobenius eigenvector of the Barycentric refinement operator. This number c(d) is very interesting for me because it is the half the mean of the universal Barycentric limit measure in dimension d. In dimension d=1, it is c(1)=1, in dimension 2 it is c(2)=3. In 3 dimensions d=3, it is c(3)=13/2 which means that any sufficiently refined graph of dimension d has arboricity at least 7. In the animation put into the youtube video, I took a rather random 3-dimensional graph and took its second Barycentric refinement, then rotated it. The 3 dimensional simplex has become already a rather large 3-dimensional ball. Because it grows like (d+1)!, the lower dimensional parts (there is a 2 dimensional triangle at the bottom which twice refined produces a 2 dimensional disk). I also mention that I believe it should be relatively easy to get this down to 8 and that bringing it down to 7 (what I believe it to be the case because for manifolds it appears that the Barycentric bound is the actual arboricity), would probably require a harder analysis. I always like to get back to the Barycentric limit story because of its universality (Barycentric central limit theorem), because the tree numbers and forest numbers and tree forest ratio converge in the limit to universal numbers which have a potential theoretical flavor. Here are again the pictures of the potential and integrated density of states in dimension 1 and dimension 2. The expectation in d=1 is 2=2c(1), in dimension d=2 it is 6 =2c(2) =2*3 (“three trees suffice!”).
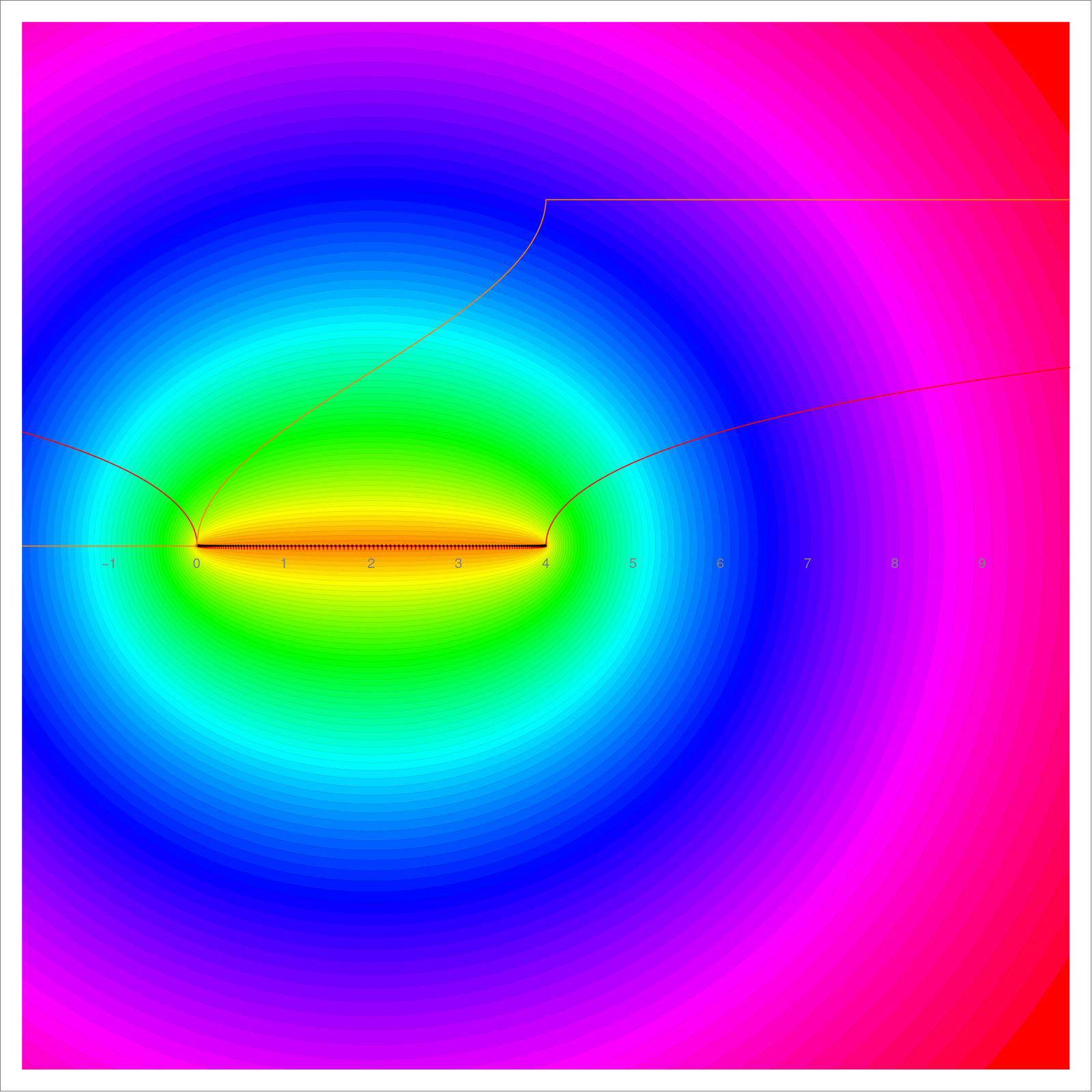
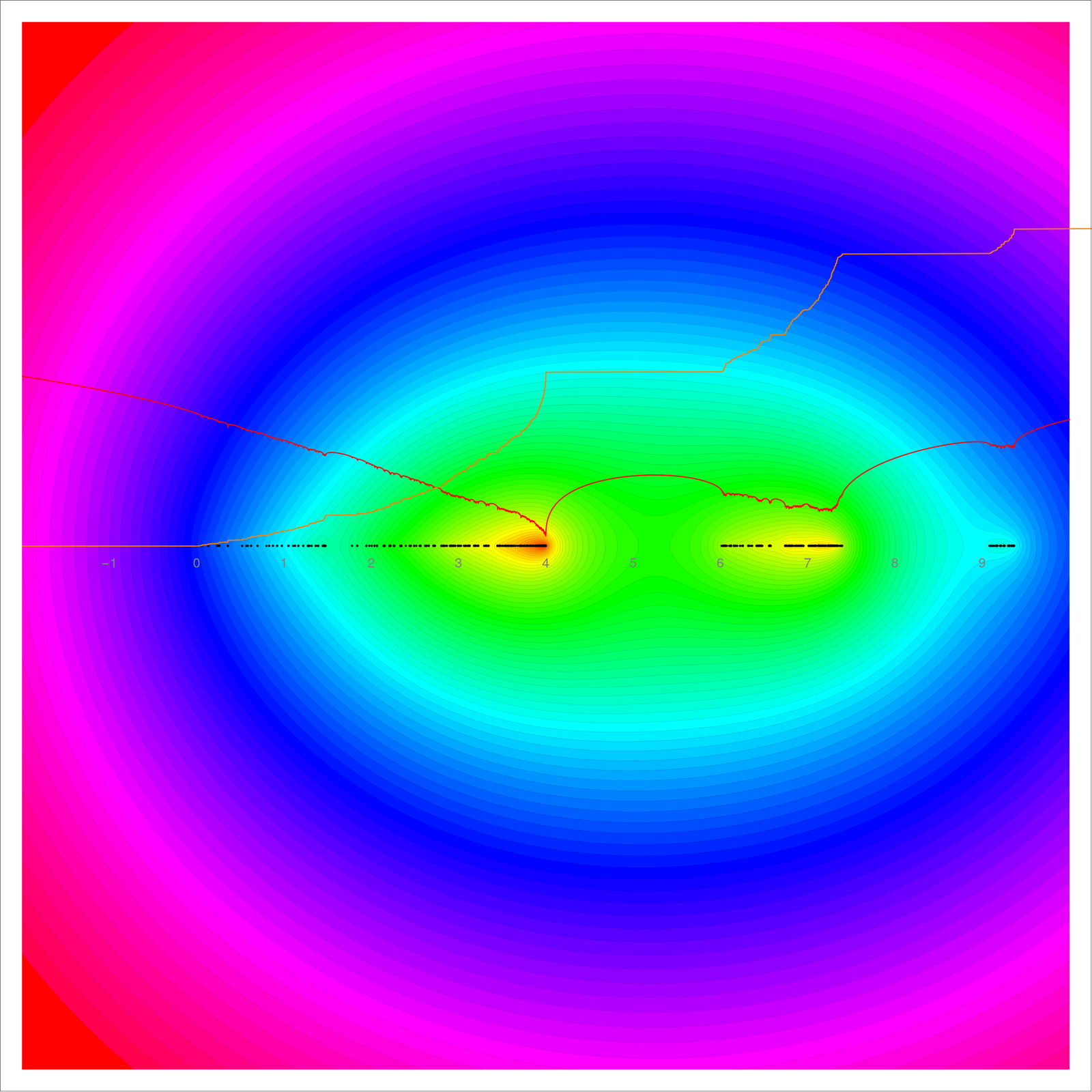
This is an other working talk organizing my thoughts about the arboricity problem currently under investigation (which I got to recently in the context of Lusternik-Schnirelmann theory whicih is also a packing problem and which is attractive to me because of its relation with the chromatic number and also because it is poorly investigated yet). The starting point for any research is always the question “why should you investigate this?” The topic of arboricity fits very well into a very classical and central topic in mathematics: investigating numerical functionals on geometric spaces. On the chalk board, I state three important motivations: first of all, and this is at the heart of mathematics: A) It is always about theorems. Structures without theorems are of little value to me. This is similar to the statement that physical theories without predictions are of little value to me. B) It is about unsolved problems. Results about numerical quantities also lead to B) There are many unsolved questions. What is nice about unsolved questions about numerical quantities is that one can measure the progress of research well. If one understands the structure, one can predict the numbers. It is not simply mumbling about concepts. It is about getting to concrete numbers. It is almost like a caricature of Kuhn’s paradigm of falsibility and so of science. You can more likely be proven wrong when making claims about concrete numbers. A statement like that the arboricity of a 2-dimensional sphere is 3 is very concrete. Everybody can understand it and everybody can check it with examples and the theory relates to other interesting numerical quantities like the chromatic number or Euler characteristic. The statement of course could still be wrong. But then there are also proofs which can be analyzed. And C), Extremizing functionals has proven to be a successful endeavor in the past, especially in physics and economics. This is independent of fashion or fads or personality cults, (the later fueled by prizes and titles). Functionals like length, area or volumes, the divisor function or were studied since antiquity [Yes, numbers are geometric objects too: see this presentation on the integer graphs which deals with the paper about primes, graphs and cohomology. And geometric objects behave like numbers if one starts to add and multiply them like in graph arithmetic (Youtube). ]
Just to elaborate a bit on the last point (mentioned towards the end of the presentation): if you study physics, then functionals are always important. I was lucky to have great teachers in physics, teachers have have done original and ground breaking work in mathematical physics like Juerg Froehlich in Mechanics (as a sophomore), Walter Hunziker (1935-2012) in Electromagnetism and Klaus Hepp in quantum mechanics (By the way, Hunziker and Hepp were the PhD advisors of Froehlich). Even so, I went on in the field of mathematical physics myself, I was not a good student in physics. The basic 2 semester course which all mathematicians had to take was tested “open book”. I was drowning under the material. You find some student outlines from me here [337 pages densely written pages PDF]. The VMP (Verein fuer Mathematiker and Physiker) had (of course there had not been any “web” yet, distributed thousands of pages of previous exams and I made the mistake to take too much material to the exam and was too slow. Some other anecdotes about exams are told here [PDF from a talk in 2015], especially the story with Foehlich orally testing me in mechanics which did not go too well for me. The oral exam with Hunziker and Hepp was a disaster too for me: the two professors would sit on chairs in front of a board and I the student was examined by both in all of the theoretical physics, I was supposed to know. I had red part of the famous Landau course in theoretical physics which were then available as cheap subsidized books as the East German publishers would sell them for 10-20 franks (linen bound heavy books). I completely drowned in Landau and Lifshitz. Physicists just go too fast for me, they can cover a rather complex topic like representation theory in a few pages. So, I had to select in my preparations and remember well, that I just had to accept to have gaps in the things which I could put into memory. And then during the exam, I was asked about scattering theory cross sections which I just did not recall any more. So, I started to talk about the importance of functionals in physics. That kind of saved me from complete embarrassment but I got a bad (still passing) grade (because of course they realized that I did not answer the question). [By the way, in retrospect, what would have been smart to do is to forget about all these fancy books, focus on what has been taught in lectures and also learn a bit about the interests of the examiners. Hunziker for example was a specialist in scattering theory. I should have been able to predict what was asked. Why the heck bother with quantum field theory if you know that this is not the focus of the examiners?]
In any case, functionals in physics are important: Lagrangian mechanics is based on the Lagrangian functionals, Hamiltonian dynamics on the Hamiltonian, heat phenomena on functionals like entropy, enthalpy, energy or temperature and wave phenomena on minimizing distances, geodesics, relativity on the Hilbert functional producing the Einstein equations. The standard model in particle physics is essentially about one particular functional. A rather big naive dream of physics is to find an ultimate functional which when extremized produces a unified theory of everything. That is naive because it might simply not exist. But it is a romantic dream.
A little bit out of context, here are the universal Barycentric limiting measures in the case of the connection Laplacian which is the matrix L(x,y) = 1 if x and y intersect and L(x,y)=0 else. The matrix L has the same size than the Hodge Laplacian 
