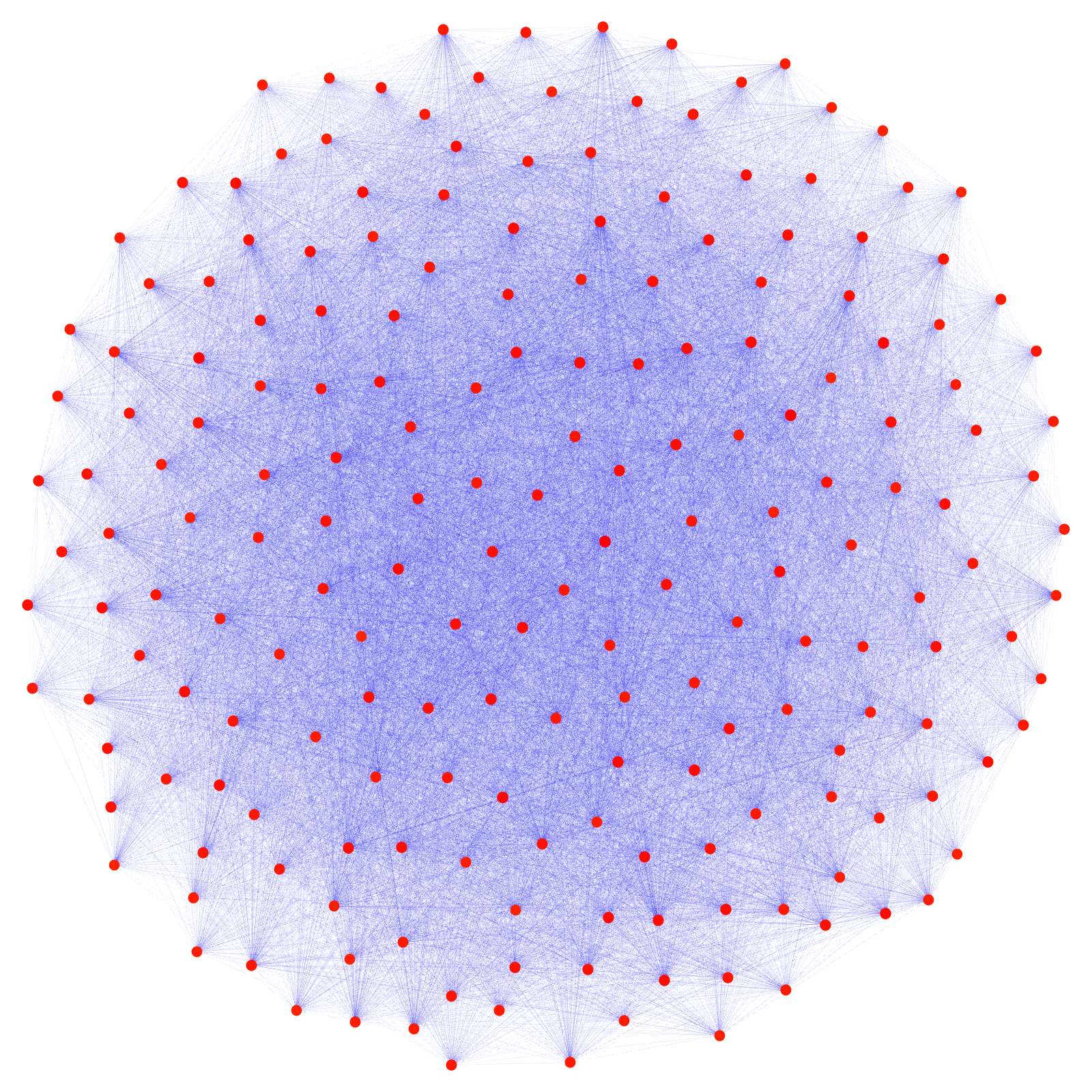
Arithmetic with networks - Quantum Calculus

[June 9, 2017: Unique additive prime factorization holds: seee here. The primes are the graphs for which the complement is connected.]

The join operation in graph theory allows to use graphs to do computation. It extends the arithmetic of integers in a natural way. We start to look at the problem of unique prime factorization in this monoid. (This section emerged, when preparing for a workshop on “The adventure of teaching algebra”. There, I also brought up the role of creativity of the teacher. I believe it is silly to preach anything about creativity if one does not walk the talk. The content below seems not have been appeared anywhere already. Anyway, it emerged through hard work in my Frac Lab …. and has been mentioned at the workshop. My Frac Lab was also proudly mentioned at the intro meeting for math21b.)

A monoid is an algebraic structure which generalizes the concept of a group. It does not assume its elements to have an inverse. But it satisfies associativity and it possesses a unit element. The prototype of a monoid is the set N={1,2,3,4,….} of natural numbers with the multiplication operation. Its unit is 1. It is associative $(a*b)*c=a*(b*c)$ . One of the first facts which mathematicians have observed, possibly even before geometry was done is the concept of a prime number, a number in a monoid different from the unit which can not be factored any further. In N, the primes {2,3,5,7,11,…} have been known since thousands of years. It was Euclid who first realized that there is something to prove here. His famous proof of the infinitude of primes (assume there are only finitely many $p_1, \dots ,p_k$ , then form $n=p_1 p_2 \dots p_k+1$ which has to be prime or have a larger prime factor than $p_k$ ) uses addition and so the entire ring structure on N. It is not a proof done entirely in the monoid itself. Euclid also knew (and used in his proof) that every number has a prime factorization. What he did not know yet (and possibly did not worry about), is whether the factorization is unique. Euclid’s lemma comes close but he does not prove unique prime factorization with it. It was André Weil who seemed have made this historical observation first in his book of 1984. It seems today that only in 1798, with Gauss’s “Disquisitiones Arithmetica”, that the unique prime factorization got really settled. Since then, we have learned a great deal more about unique factorization domains and rings of numbers in which unique prime factorization fails. In the ring $Z[-\sqrt{5}]$ for example we have $6=2 \cdot 3 = (1+\sqrt{-5})(1-\sqrt{-5})$ and unique prime factorization does not hold. We want to look of course at the analogue question for the new primes, primes in graph theory. Unfortunately we still are only in the stage of Euclid. It will need some time to get to the level of Gauss (Hopefully not 3000 years!). But one goal is definitely a “fundamental theorem of graph arithmetic”.

Multiplying networks

In order to define the monoid of networks, we first have to define the objects. The objects are finite simple graphs G=(V,E) with vertices V and undirected edges E. “Simple” means especially that there are no self-loops nor multiple connections. The multiplication is defined by the join

Definition: The join G*H Is defined as G*H=(V(G) union V(H), E(G) union E(H) union { (a,b) | a in V(G) and b in V(H) }.

This definition of a join seems first have been done in 1949 by A.A. Zykov in graph theory. [Zykov is also an author of a book in graph theory: google link, in this presentation the product is called Zykov product. Will see whether I can dig more about that.] I have used the product a lot already in my own work but the product seems not have been appeared much in graph theory yet. The join operation was again central recently when proving that the unit sphere topology of a simplicial complex is a combinatorial invariant and agrees with the Green function values of the Fredholm matrix of the connection graph.

What does the “join” mean intuitively? It means that we take the two graphs as a disjoint copy, then connect any pair of nodes which belong to different graphs. The join product is clearly associative and has a neutral element, the empty graph $(\emptyset,\emptyset)$ .

Fact: The category of finite simple graphs with the join operation is a monoid.

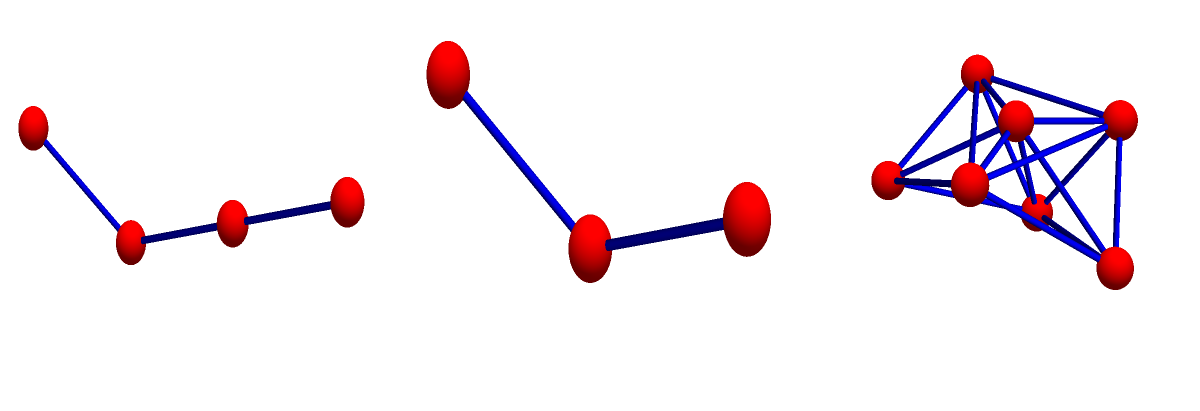
We don’t care that it is not the multiplicative monoid of a ring with unit (there might be no natural addition which comes with that multiplication rendering it a ring). Lets look at some examples of products: the first graph is G, the second graph is H, the third graph is G*H:

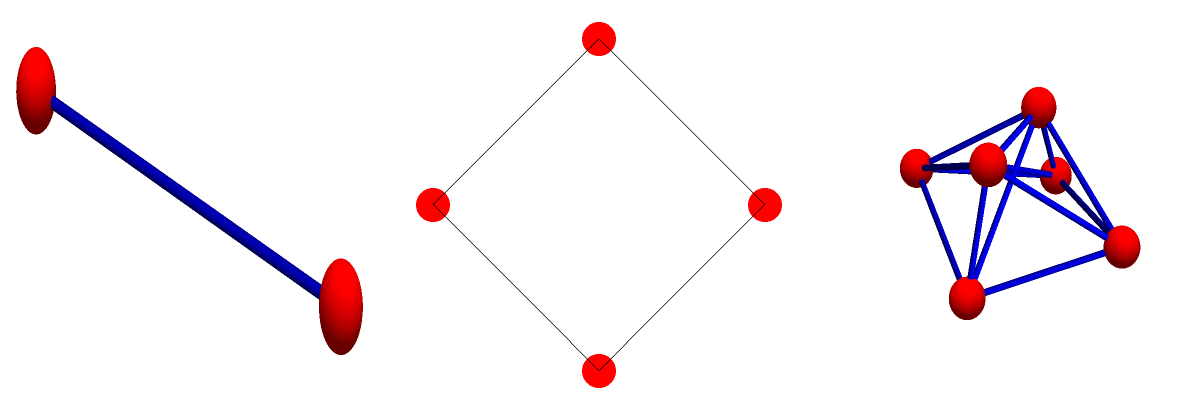
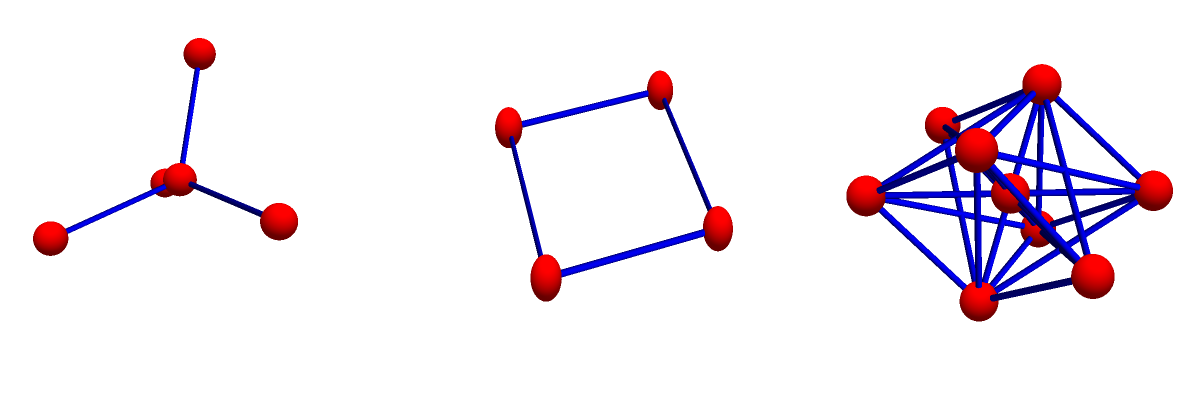
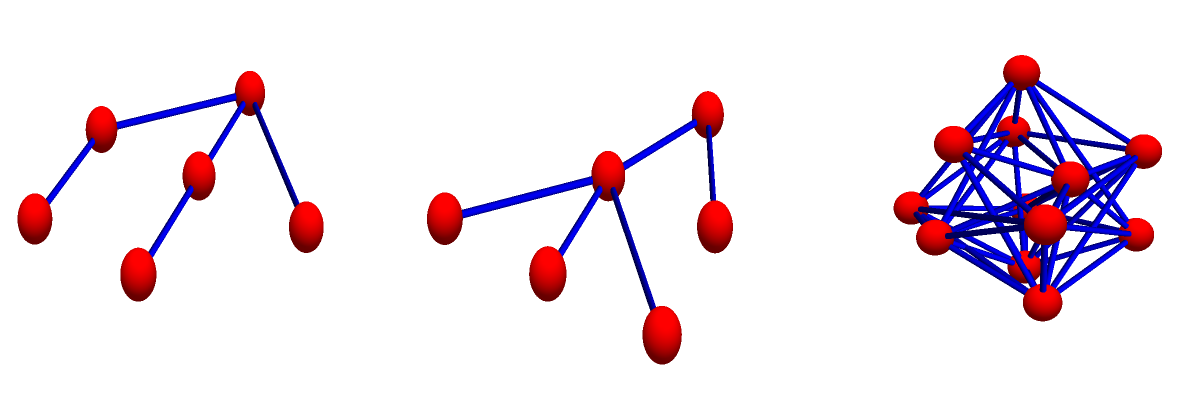
Analogue of Euclid lemma

Definition. Lets call a graph G a prime graph if it can not be written as G=H*K, with graphs H,K different from the empty graph.

As in the case of the natural numbers, a unit unit is not considered to be a prime. We can now enjoy doing explorations similarly as 3000 years ago just in a realm where we have no idea yet where we are going because nobody has been there. Its very exciting.

Definition. The maximal dimension of a graph is d if there is a complete subgraph with d+1 nodes but no complete subgraph with d+2 nodes. The empty graph has dimension -1.

We call this complete graph K_d+1. The dimension of a graph without edges and at least one vertex is 0. The maximal simplex is also called a facet and the number d+1 the clique number. Any complete subgraph is also called a simplex or clique or face. Because $K_n * K_m = K_{n+m}$ we have the formula:

Dimension formula: dim(G * H) = dim(G) + dim(H) + 1.

By the way, there is a more advanced notion of dimension, the average of the dimensions of the unit spheres plus 1, which we call the inductive dimension and which is very useful and natural but which takes also non-integer values. With this dimension, we have dim(G*H) larger or equal than dim(G) + dim(H) +1, a similar formula as known for the Cartesian product but were we don’t have a “+1” term. Dimension allows to see:

Euclid type Lemma: Every graph G has a factorization into prime graphs.

Proof. We use induction with respect to dimension. For zero-dimensional graphs it is clear already. If there is no factor of G besides the empty graph, then G is prime itself. Otherwise, we can write G=H*K. Now because of the dimension formula, both H and K have dimension smaller than G. By induction assumption, they can be factored into prime factors $H = P_1 \dots P_k$ and $K = Q_1 \dots Q_m$ . We have now the prime factorization $G=P_1 \dots P_k Q_1 \dots Q_m$ . QED.

The infinitude of primes

The dimension formula already establishes that there are infinitely many prime graphs. Every graph $P_n$ with n vertices and no edges is prime. But we can do better than that. First of all, we have to know more about the cardinalities of the complete subgraphs of G.

Definition: The f-vector v= (v₀,v₁,…, v_d) of a graph G, has as coordinates v_k,the number of complete subgraphs of dimension k of G.

Definition: The Euler characteristic of G is defined as X(G) = v₀-v₁+ … +(-1)^k v_k.

What happens with the f-vector or Euler characteristic of a product? This is best described with a function

Definition: The extended Euler polynomial of a graph G is f_G(x) = 1/x + v₀ + v₁ x + v₂ x² + …

It is called “extended” because without 1/x it is called the Euler polynomial e(x)=v₀ + v₁ x + v₂ x² + … which is a generating function for the f-vector too). Now, with the 1/x term its technically not a polynomial any more. Here is a beautiful formula recently discovered. I was unable to spot it yet but the graph theory and combinatorial topology literature is huge.

Counting formula: f_G*H(x) = x f_G(x) f_H(x).

Proof. Just look at individual simplices and note that every k-simplex joined with a m-simplex is a (k+m+1) simplex.

[Jan 28. June Hu Fung pointed out that it is easier to look at x f(x) and use the usual multiplication. This makes it more likely to be known. I leave it for now in the old form here].

It implies for example that if $G=P_n$ and $H=P_m$ where $f_P(x) = 1/x+n$ and $f_H(x) = 1/x+m$ then $f_{P*H}(x) = 1/x + m+n + m n x$ . We see that if a one-dimensional graph has a prime number of edges, then it must be prime. We can also see in general that any circular graph C_n with n>4 is prime. The circle C₄ is the square of the 0-sphere P₂.

Euler Characteristic formula: X(G * H) = X(G) X(H) – X(G) -X(H).

Proof. We have $\chi(G) = 1+f_G(-1)$ . QED

[Jan 28, 2017: Jun Hou Fung pointed out to me that similar relations might appear in Chern classes and that this also means that the Euler-Poincaré functional i(G) = 1-X(G) is multiplicative: i(G*H) = i(G) i(H). This fits well into the sphere spectrum story. Whether this helps to “factor a graph” is not likely since the presence of only one factor with Euler characteristic 1 produces Euler characteristic 1 for the product.]

Infinitude of primes: for any dimension d>0, there are infinitely many prime graphs of dimension d.

Proof. This follows from Euclid’s result on the infinitude of rational primes. The reason is that for any rational prime p, we just have to take a network of dimension d for which the maximal simplices have cardinality p. This is then prime. QED

Why is the join important ?

The join is one of many operations one can form on graphs but it is important because it shadows exactly the properties of the join operation in the continuum and because it is a monoid. The join of a graph with a 0-sphere for example is called the suspension of the graph. Suspensions allow to produce from spheres higher dimensional spheres. The join operation turned out to be especially useful in the Fredholm story to understand the unit sphere topology and to establish the invariance of the Green function values under Barycentric refinements. There is an other product $\times$ which resembles the Euclidean product in the continuum but which is only associative modulo some Barycentric equivalence. For the product $\times$ , the Euler characteristic is multiplicative $\chi(G \times H) = \chi(G) \chi(H)$ , the maximal dimension is additive and simplicial cohomology is compatible in the sense that the Kuenneth formula holds and that it allows to look at de Rham cohomology which is computationally less expensive than simplicial cohomology. There are other products, the traditional Cartesian product as well as the tensor product.

I like both the graph product as well as the join because they both have almost exactly the same properties than the Cartesian product or the join product in topology classical topology. The join is singled out by two facts: it is a monoid and then it has the same properties than in the continuum (sphere invariance, correct in dimension and associative). Both the join and the graph product are important in the Fredholm story, especially when analyzing the unit spheres in Barycentric refinements. A crucial fact was that the unit sphere of the Barycentric refinement is always the join of two graphs, the stable and unstable sphere. In the analysis of the topology of unit spheres, I had this winter to go a bit deeper even and analyze the structure more carefully (using the join operation).

An important question

The classical fundamental theorem of arithmetic assures that the monoid N of natural numbers enjoys unique prime factorization. Is this true for graphs? We don’t know. So far, it is true in all cases we have seen, but this could be misleading.

Question: Does the monoid (Graphs,*) have a unique prime factorization?

The monoid of graphs has many interesting sub-monoids. One particularly important example is
the sub-monoid of spheres, where the question can be asked too and which is possibly more accessible. I know for example that any one-dimensional graph which is not prime has a unique prime factorization. The notion of a sphere can be done entirely combinatorically, we don’t need any realization of the simplicial complex in an Euclidean space. We take here the point of view of the Pythagoreans and warship the finite structures, as computer scientists do naturally. The following definition is essentially due to Evako. It defines spheres recursively without referring to any continuum. (In combinatorics it can be healthy to stay away from anything which comes close to infinity, like Euclidean spaces. Classical topology of simplicial complexes almost always refers to some Euclidean embedding. Even simple things like Barycentric refinements are almost exclusively done in Euclidean settings in most topology books. The finite combinatorial construct is much easier to grasp, where it is just the order complex of the complex.) So, what is a sphere, if we are not allowed to say things like “a triangulation of an Euclidean sphere”?

Definition. A graph is a d-sphere, if every unit sphere S(x) in the graph is a (d-1)-sphere and if taking away one vertex, then the graph is contractible. Also inductively, a graph is contractible if there exists a vertex x with contractible unit sphere which when taken way, produces a contractible graph.

Invariance of spheres: the join of a n-sphere G and a m-sphere H is a (n+m+1)-sphere G*H.

Proof. Unit spheres remain spheres because S(x) * H is the unit sphere in G*H for a vertex x in G and G * S(y) is the unit sphere for a vertex y in H. Use the fact that the join of a contractible graph with an other graph is contractible to see that if we take a vertex away from G*H, then the rest is contractible.

Question: Does the monoid (Spheres, *) have a unique prime factorization?

Note that the answer to this question is clearly “No” in the continuum as we can write for example a 5-sphere as a join of a 2-sphere and an other 2-sphere or as a 1-sphere with a 3-sphere. The arithmetic question is only interesting in the discrete.

Overview over products

All of these products $\oplus$ , $\times$ , $\otimes$ and $*$ are associative.(For the Cartesian product $\times$ associativity only holds modulo topological equivalence. For example, $G \times (K_1 \times K_1) = G \times K_1 = G_1$ is the Barycentric refinement of G, while $(G \times K_1) \times K_1 = G_2$ is the second Barycentric refinement of G.) The old graph product has $K_1$ as a one element, the new graph product does not have a unit. Multiplication with $K_1$ is the Barycentric refinement. 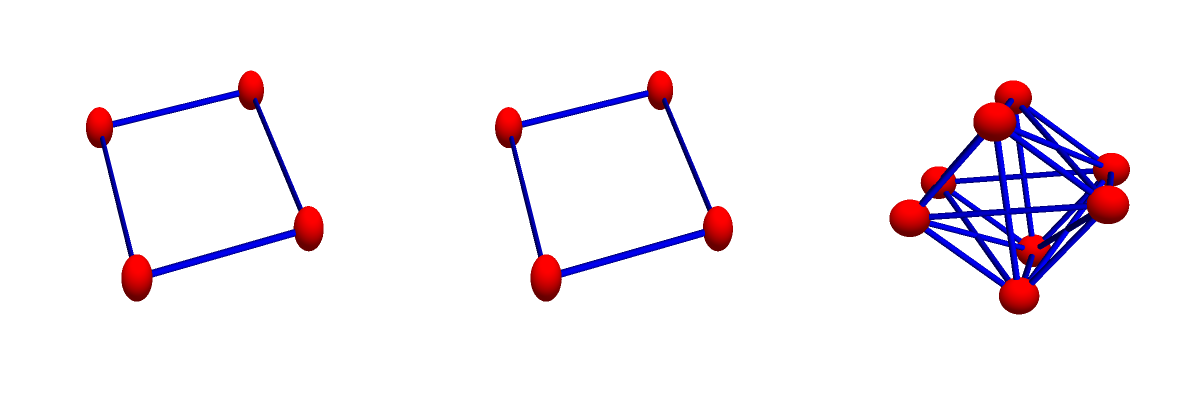The tensor product has $K_1$ as unit. Here are examples of the classical 1D Cartesian product, the natural Cartesian product, the tensor product and the join product:

Old Cartesian Product: (is really only useful if you consider graphs one-dimensional objects, it disregards cohomology, dimension, has nothing to do with the continuum. Yes, the product of two linear graphs is a lattice as in the picture, but that is only because we imagine the holes to be filled and be a picture for a 2D lattice. Figuring out which are the “holes” in this case was easy. If we multiply two arbitrary networks, this is no more clear.)

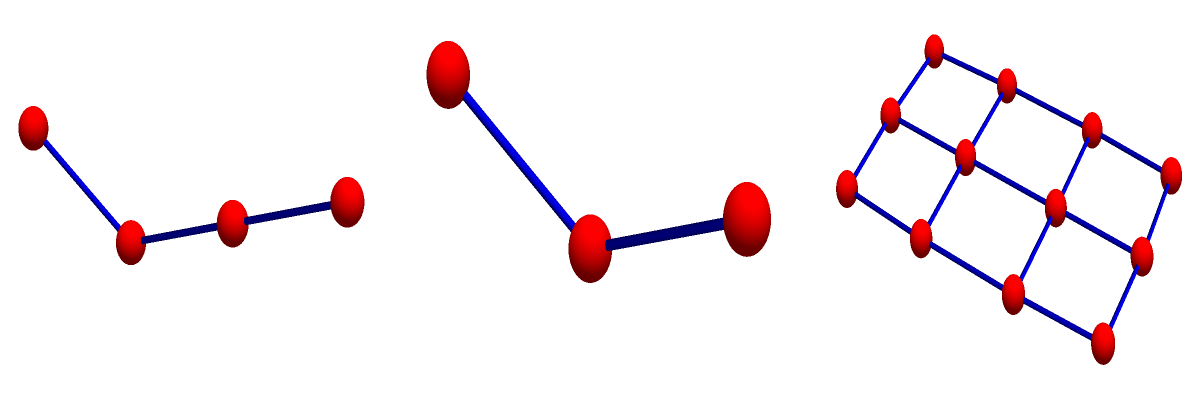
Cartesian Product: (corresponds to product in the continuum, respects cohomology, dimension, Euler characteristic multiplicity. It allows to do geometry as in the continuum. A special case, the product with a 1-point graph K₁ produces the Barycentric refinement. )

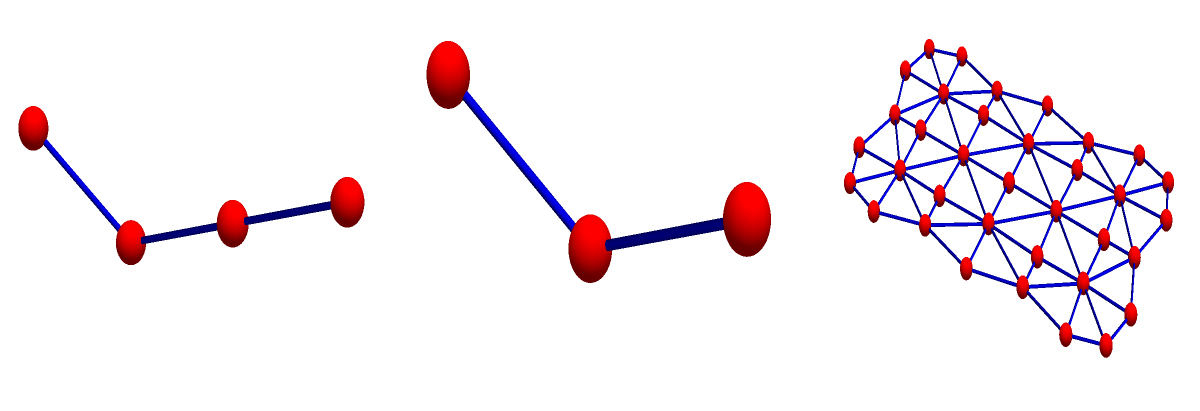
Tensor Product: (is of one dimensional nature also: it has the nice property that the Adjacency matrices are the tensor product. But adjacency matrices only encode one dimensional parts of the graph. The tensor product of graphs is not that natural if we do geometry and see graphs as grown up structures allowing to do geometry as we know it in the continuum. )

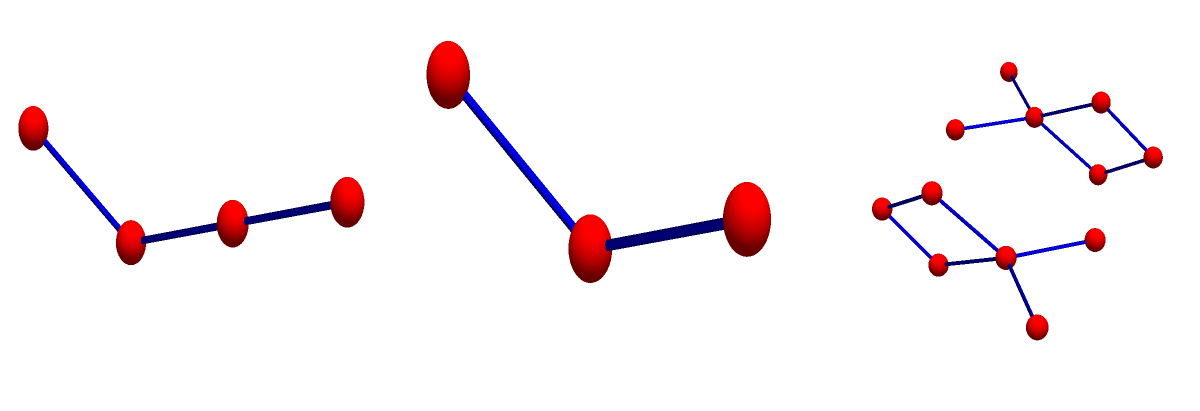
Join Product: (corresponds exactly to the join product in the continuum, preserves spheres, has natural Euclidean and Euler polynomial formula as well as behaves well with dimension, also the volume, the number of maximal simplices is multiplicative, it also has a nice algebraic description. Important graphs like the utility graphs P₃ * P₃ are join products):

The quest of finding an additive structure

Update of January 15. Still struggle with the question:

Is there an additive structure compatible with the monoid (Graphs,*) which produces
an abelian ring? What is the zero element?

[ By the way, I also struggled with the web editor in word press, I had written all morning a longer extended version of the following and the editor ate all (a buggy newly installed plug-in I had tried out malfunctioned and destroyed everything. I could not even retrieve a backup. Everything lost. Nothing even in the cache of the web browser). I know that using online editors is a terrible idea but I never seem to learn. But this blog got actually started to learn more about CMS. I still hate web editors but you are not qualified to hate something really, if you don’t know them. ]

History indicates that finding the additive 0 element and negative numbers was harder than building fractions the multiplicative inverse. The Egyptian mathematicians have known fractions already but the 0 came only later. Yes, it was implicit in Sumerian Cuneiform writings and also in Mayan mathematics as a place holder but the zero element itself seemed first has got established as a number in Indian mathematics. Its an interesting story and somehow, we can feel like our ancestors here as we don’t know what is zero, nor do we know what negative graphs are!

We can learn a lot from history. In building up number systems one always has used Cartesian products. For building fractions we define (a,b) + (c,d) = (ad+bc,bd) and (a,b)*(c,d) = (ac,bd). When building imaginary numbers we define (a,b)+(c,d) = (a+c,b+d) and (a,b)*(c,d) = (ac-bd,ad+bc). The Cayley-Dickson picture of building Quaternions or Octonions uses the same trick. An other construct is the “Numbers and Games” construction of Conway for which I really can recommend the booklet “the island of numbers” by Donald Knuth. When I was reading that in high school, I found it a great adventure.

[ January 24 addition: Even so I did not get through the book of Knuth (as I spent my time at that time mostly with research on Partitions of numbers then). Similarly than challenging computer games, it is essentially a research task to figure out things in the Knuth novel. The book “numbers and games” of Conway serves then as sort of a solution manual. Sometimes there is just not enough time. Like with computer games where this happens frequently to me. At Caltech, I got addicted for weeks to “Myst”, a riddle based adventure game. Even so working hard on Myst at nights and keeping a diary about the possible riddles, I eventually bought the solution book to get freed from that spell. As a postdoc in a group, where your mentor writes 15 articles per year, there is not much time for games ].

It was Grothendieck who formalized the construction of groups from monoids in the most general form. His construction of an Abelian group from an Abelian monoid uses also the Cartesian product construction. Lets mention it, as it is related to prime factorization.

Grothendieck group: There is an Abelian group (Graphs x Graphs,*) which contains the monoid (graphs,*).

Proof. The Abelian group contains as elements pairs of graphs (A,B) and multiplies them as (A,B)*(C,D) with (AC,BD) then forms equivalence classes. Two pairs (A,B) ~ (C,D) are identified if there exists a graph U such that ADU = BCU. We see that if we have a unique prime factorization, then we can identify elements in the group as reduced pairs (A,B), where A,B have no common factor. This is completely equivalent to the identification of 2/6 with 1/3 in school algebra. The Grothendieck construct is a fancy way to write “fractions”!

Now, back to the question of zero and missing addition. The algebraic counting function 1/x + a + b x + …, we have used to count simplices in the product associates the 1 element with 1/x. Indeed with the multiplication f*g(x) = x f(x) g(x), the element 1/x is the one element! It is clear that the 0 element will have to be associated with the 0 in that generating function picture. So, since the one element and the zero element must be different, we can not have that the 0 element is given by the empty graph. Indeed, the zero element must be something new. Lets take the point of view that the zero graph is really a graph object. It is the -1 sphere and not the empty set. Maybe we should think about the empty set as the zero element and the empty graph as the 1 element. But what is the addition?

Well we have already a natural extension of graphs to an additive group. This has been done by Poincaré around 1890. It is the concept of a chain. This is probably best seen algebraically. The triangular graph for example is represented in the Stanley Reisner picture using polynomials. (I myself was lead to this when searching for a product compatible with cohomology: See this paper). A triangle for example is represented in that ring as x+y+z+xy+xz+yz+xyz. For every simplex in the graph there is a monoid. One can now naturally compute with the ring elements rather with graphs. The group of chains introduced by Poincaré is related. Poincaré would for example look at objects 3x + 5y-z + xy – 8 xz – 3 yz + 2 xyz which is a chain. There is a natural boundary operation d which satisfies $d \circ d=0$ and which therefore allows to look at cycles given by the kernel of d and boundaries given by the image of d and then form the homology groups as usual. We don’t here go into this but just note that there is a natural additive group of chains which extends the category of graphs and which produces an Abelian group which is part of a ring, the Stanley-Reisner ring. Now, Euler characteristic is an additive functional on this ring and also satisfies X( A x B) = X(A) X(B) if we take the Cartesian product. Note however that the Cartesian product is not a monoid. It is associative but has no 1 element. The 1 element must therefore be considered a prime number there but this is a problem as K₁ x K_₁ = K₁. So, unlike the join multiplication *, the Cartesian multiplication x does not have an interesting arithmetic. In our case however, we have a different operation, the join, which has a nice 1 element. Lets describe the empty graph with 1 and the zero element with 0. We look now a t elements of the form a+f, where f is the Stanley-Reisner picture. To calculate, we compute as usual. What is 0? Its not the empty graph. There is a nice episode in the story The confusions of young Toerless by Robert Musil, which explains a bit this confusion (the mathematical confusion is much less serious in that novel than other confusions). So, lets postulate that these algebraic extended Stanley-Reisner objects now represent our new objects generalizing graphs. The addition is the usual addition of rational functions in several variables where the ideal generated by squares is modded out. We can just multiply

(1+a) (1+u + v + u v) = 1 + a + u + a u + v + a v + u v + a u v

Observation: The join multiplication is very natural algebraically. It is essentially the multiplication in the Stanley-Reisner ring, but where a 1 element is added to the objects.

One difficult is that if we want to get the join, we have to multiply different vertex sets using different variables. Multiplying the same K₁ by itself gives (1+u)(1+u) = 1+2u+u² = 1 + 2u. While adding it gives 1+u + 1+ u = 2 + 2u. So, we are still not happy as for a ring structure, we need to be able to multiply anything with anything and do not have to insist that the objects are different. One possibility is to represent every ring element as something like
1 + x( a + b + c + ab +bc + ca)
where every ring element has a different variable x then insist on x² = 0 for all these auxiliary variables. The problem is that we have now many cases where X*X=0 and that the prime factorization is less natural in that extended setup. Writing K₂=K₁ K₁ for example assumes that on the right hand side we have different objects (a kind of Pauli Principle), but still the result assumes two graphs to be equal when they are isomorphic. Well, in any case, the just outlined connection with the Stanley-Reisner pictures shows how natural the join multiplication is as it is essentially the multiplication in that ring. But for the arithmetic question posed, we take a bit of an other point of view. We see for example the graph K_n as the n’th power of K₁. But in that power, like an exterior power, we build up new vertices. Its a bit like in particle physics, the elementary particles are all the same but they can not be in the same state by the exclusion principle. In any way, enough written for now. The question of unique prime factorization remains.

Relation with Fredholm characteristic

The above formula for Euler characteristic shows that graphs with even Euler characteristic form a sub-monoid of (Graphs,*) and graphs with odd Euler characteristic also form a sub-monoid. Euler characteristic so produces a natural split of the monoid. Now here is an other elementary observation. I have called the Fermi characteristic of a complex (and especially of a graph euiped with the Whitney complex) to be the product of (-1)^{dim(x) where x runs over all subsimplices. It is 1 if there exists an even number of odd dimensional simplices, otherwise, it is -1.}

In the sub-monoid of graphs with odd Euler characteristic, the graphs with Fermi characteristic 1 must be prime in that monoid.

Proof. Just check that in each case, the product has Fredholm characteristic -1. QED.

In the sub-monoid of graphs with even Euler characteristic, the Fermi characteristic is multiplicative.

Proof. Also this, is just to look at cases, using X(G) = b-f and that the Fredholm characteristic is 1 if and only if f is even. QED.

Example: the graph K₁ has Fredholm characteristic 1 and Euler characteristic 1. It is prime.

Finally, we can mention there is an other sub-monoid, the sub-monoid of graphs with Euler characteristic 0 or 2. It contains the monoid of spheres.

By the way, the Grothendieck construction can be applied to the sphere monoid leading to a sphere group. It is a large group.

An other thought about building a ring

We have seen that we the join multiplication can be written nicely by representing a graph as a function in the same number of variables than vertices. This is the Stanley-Reisner picture. So, a triangle for example is f=1+x+y+z+xy+yz+xz+xyz. Now, if we take the product of two such graphs, we automatically have to assume that the variables in the different graphs are different. Now, when looking at the sum, we are tempted to use the usual sum in polynomials. But that is not the right sum if we want to end up with a graph again. If we think about the disjoint union of graphs as a sum, then this is a nice monoid but it again has the empty graph as the zero element. We want 0 as the zero element (which is not the same thing than 1, which is the empty graph). So, what do we do? We might want to start with the disjoint union as a sum but not take the disjoint union of empty graphs. We have therefore for example K₂ + C₄ = (1_+ x_+y +xy ) + (1+a+b+c+d+ab+bc+cd+da) = 2+x+y+xy+a+b+c+d+ab+bc+cd+da. This is now an additive monoid with 0. The negative elements are now new objects like (-1-x-y-xy) = – K₂. Now we have a commutative ring which is an integral domain. The problem is that the disjoint sum is not distributive: G*(A+B) = G*A + G*B can not be true as the left hand side is connected and the right hand side is not connected. But the question remains:

How can we build a natural ring?

What we would like for a ring of graphs is that the Euler characteristic is additive and since with multiplication satisfies X(G*H)=X(G) + X(H)-X(G) X(H) also the sub-monoid of graphs with even Euler characteristic is invariant. We can build the field of fractions of this ring. Can we extend Euler characteristic to the field of fractions? It would continue to have to be additive and satisfy the same determinant formula.

A cryptology problem

January 16. The primes are useful for cryptological reasons in number theory. There are two problems which are both hard there. The first is the discrete log problem (which is useful for Diffie-Hellman), then there is the factorization problem which is useful for RSA. How hard are these problems for graphs?

How hard is it to factor a graph G*H, where G,H are both prime graphs of size n.

Here is an example of a product. We just chose two random graphs with 100 nodes and produced the product. They both have 2475 edges. The product graph has 14950 edges.

[I just found an other reason why to hate editors in browsers. After uploading the picture above, the browser crashed, again taking with it all edits. If using a solid editor like vi or emacs in a terminal, there are always backups available even if something should crash (which almost never does). Still, in this on-line editor, if I “update” the file, the page reloads again at the beginning, and I have to scroll down again. There are lots of other short comings, like the lack of doing bulk replacements or structuring text visually (a new line produces a new paragraph). There is one advantage of on-line editors, that one could work on a page independent of the operating system, even from a phone, even so editing even from a tablet is abusing it.]

An other question, which has been solved in the integers N is whether it is hard to verify that an object is prime:

How hard is it to establish whether a given graph G of size n is prime?

There is a simple way to generate prime graphs. Just make sure the volume the number of maximal simplices is prime. The reason is that the volumes of graphs multiply when taking join products. While trivial, lets still state that:

If a graph G has a volume which is a rational prime and if the graph is not a pyramid over a smaller graph, then the graph is prime.

Proof. The explicit formula for the f-vector generating functions shows that Vol(G*H) = Vol(G) Vol(H), where Vol(G) is the last entry in the f-vector of a graph. There is a slight difficulty with the prime factor K₁ which has volume 1. But such a prime factor means that the graph is a pyramid construction over a vertex. QED.

Maybe we should also mention that any graph product G*H can be written as $P(G)*P(H) \cup G \cup H$ , where P(G) is the graph G in which all edges have been taken away. Now, P(G) * P(H) is a bipartite graph making the connections between different parts. So,

A product graph G*H contains a bipartite subgraph with the same number of vertices than G*H.

Wheater this is useful for establishing whether a graph is prime or not or to find a prime factor is not clear. But what one can do is take the graph which needs to be factored, then look at all possible partitions of the vertex set into two parts (which is quadratic in the size of the graph), the see whether the bipartite graph P(G)*P(H) is part of the graph. Maybe this should be the analogue of the “Baby test”.

If a graph G does not contain any of the bipartite graphs P(A) * P(B), where $A \cup B$ is a partition of the vertex set V(G) into two disjoint non-empty sets, then it is prime.

So, checking whether a graph is prime should not be as costly after all as it is polynomial in the number of vertices in G. If we find a bipartite subgraph P(A)*P(B) then we also have found a factorization as we can take the graph H generated by A in G and the graph K generated by B in G and have G= H*K.

Establishing that a graph is prime in (Graphs,*) is a task which is polynomial in the number of vertices. Also the task to factor a graph G=H*K where H,K are prime is polynomial in the size of the vertex set of G.

So, graph cryptography might not be as useful. One could have hoped that there are difficult problems like the graph isomorphism problem or the clique problem which is part of the problem of factoring in (graphs,*) but that seems not to be the case and one would really need very large graphs to have a difficult factorization task.

The search for bipartite subgraphs P(A)*P(B) could also be the key to establish the fundamental theorem of arithmetic for graphs. We just have to show that we can not have simultaneously two graphs P(A)*P(B) and P(U)*P(V) contained in the graph G, where U,V and A,B are two different partitions of the vertex set V into two sets [Different in the sense that not just A is a subset of U or V for example ].

I have in the last couple of days also looked at the question how to do modular arithmetic as this is really useful in cryptology. One possibility is to take a background graph P which is prime and then reuse old vertices when making the product. So far things do not work yet. I have no idea yet how to do modular arithmetic on graphs.

[ Just as a bit of nostalgia. In Switzerland, where military service is mandatory, I was first driving M109 tanks in the artillery, which was a lot of fun. Later, I could join the cryptology group which was even better. Every year, in the WK (repetition course), we would spend 3 weeks per year in some beautiful place and do cryptology. We had been in beautiful locations like Oberburg in the valley of Emmental or in Linden or Chatel Saint Denis. All gorgeous places to be, to make hikes or run and of course do some cryptology or discuss math and computer science with other mathematicians and computer scientists (both from academia or industry) in coffee shops. Unfortunately, I don’t have material from there any more as we had to give back any text material (some of it was excellent) or even burn our notes. There had especially been an in house cryptology book which I would love to have. But what was done is of course not a secret, as every cryptology unit in the world looks at that. One thing which might appear a bit funny now is that all the big integer arithmetic or elliptic curve arithmetic etc had been done and was maintained “in house”, from scratch, in Pascal on a machine away from the web. There was a computer science, a statistic and a mathematics unit. I myself worked in a team implementing all the integer factorization algorithms like Pollard, Morrison Brillart or the Quadratic Sieve, and later on discrete log problems. One of the members had brought his Next machine which I immediately fell in love in and bought one myself. By the way, having 3 weeks in the year with additional pay (the military pays an additional salary and having not to buy any food etc allowed me to shell out the 6000 swiss franks then for that computer with laser printer). Why did the NeXt computer fail? It might have been too expensive, but it was also too perfect [At that time, one of the reasons for the success of the PC was that it was an eldorado for developers to produce programs which do things which are ridiculously trivial in a unix environment like connecting to the machine remotely – and then of course games. Also, for geeks it can often be more attractive to have things not work at first as this produces a challenge. Linux had initially that “feature”. The last 15 years or so, the expectations have changed. It came from the emergence of “phone computers” of course, which just work. Having an operating system which crashes is almost unthinkable nowadays and only bareable for masochists]. Everything worked on the NeXt. It came with essentially anything which was needed: like GNU tools, Latex or Mathematica, had already rendered everything in Postscript, one did not have to do any sys administration. Of course the hardware was also fantastic. And it was already a stable Unix environment. When Apple became stronger (and NeXt disappeared, a traumatic experience for me), I had bought for a couple of years a Unix application (called Mach X) for the mac, which still allowed me to work on a Mac laptop like on a Unix workstation. Then came the time, when I bought also a Sun workstation (which were great hardware, but Solaris was not so much my thing). Since OSX came out and Linux grew up, the operating system problem has been solved. We are lucky. It could easily have gone the other way and we would live in a PC mono culture hell, where the web would look like a cable network service requiring the user to buy access to services and where brouwsers would modify the content according to the service you access. ]

More remarks

The prime factor K₁ is special and prevents from claiming that for a prime graph, the volume has to be prime. The example of a circular graph S₆ is the smallest example of a graph which is prime evenso the volume is not prime and the star graph S₅ is the smallest example of a graph which is not prime even so the volume is prime. We mentioned the dimension formula. Its better to use the clique number c(G) = dim(G)+1.

The clique number is an additive integer valued functional on the monoid of networks: d(G*H) = d(G) + d(H).

Lets focus on graphs which are not a pyramid construction over a vertex (which excludes the prime factor K₁). Now, the volume indicates the volumes of the factors. If a graph has given volume V and clique number c, we know now that the volumes of the primes satisfies V(P1) V(P2) … V(Pn) = V(G) and the clique numbers satisfy c(P1)+…+C(Pn)=c(G). By the unique prime factorization for integers, we know now the volumes of the factors. But this does not yet assure that we have a unique prime factorization for G.

Zeta function and prime growth

For rational primes, there is a nice zeta function $\zeta(s) = \prod_p (1-1/p^s)^{-1}$ . Independent of the unique prime factorization question, we can try to defint his for networks. But even if we can define a good ring, this zeta function takes now values in a weird space of network limits. One will then have to define notions like analytic continuation for functions taking values in those spaces.

A bit more down to earth, one can also look at the problem how fast the number of primes grow. A concrete combinatorial problem is already to find the number of prime graphs for a given class of networks with n vertices.

How fast do the number of prime networks in the class of all networks of size n grow?

As we defined things so far, since any product H*K is a connected graph we have:

Any disconnected graph is prime.

Maybe the prime counting function should count the number of connected prime graphs. Its easy to see that also among connected graphs, in any dimension, the number of connected prime graphs is infinite.

The problem of Goldbach is not very interesting in this arithmetic as how we defined it (we have just temporarily chosen the disjoint sum as an addition), the sum of two graphs is disconnected but the product of two graphs is connected. But since the disjoint union is not a good addition (as we lack distributivity), this is not a surprise.

[Jan 24: A very small submonoid of the network monoid is the one consisting of complete graphs together with the empty graph. The product of two complete graphs K_n * K_m is the graph K_n+m. Here, one has a trivial prime factorization as any element G in this monoid is of the form K₁*K₁ …* K₁. This monoid is equivalent to (N,0,+) or the submonoid of the multiplicative monoid (N,1,x) generated by a prime p. If p=2 for example, then the elements are of the form 2ⁿ with n=0,1,2,3… which by taking logs is equivalent to (N,0,+) of course.

In general, one can look at submonoid generated by a single element. Starting with P₂, the zero-dimensional sphere, the powers generate (by suspension) all topological types of spheres, but far only a small submonoid of the entire sphere monoid. We don’t generate the one-dimensional sphere C₆ for example. In all these cases of course one has a unique prime factorization.

One could look at small submonids generated by two elements. Since P₁ generates all complete graphs and P₂ all sphere types, one can look at the graphs generated by P₁ and P₂. Since multiplying by P₁ renders the graph contractible, it is also not that interesting. Also here, we still have a unique prime factorization.

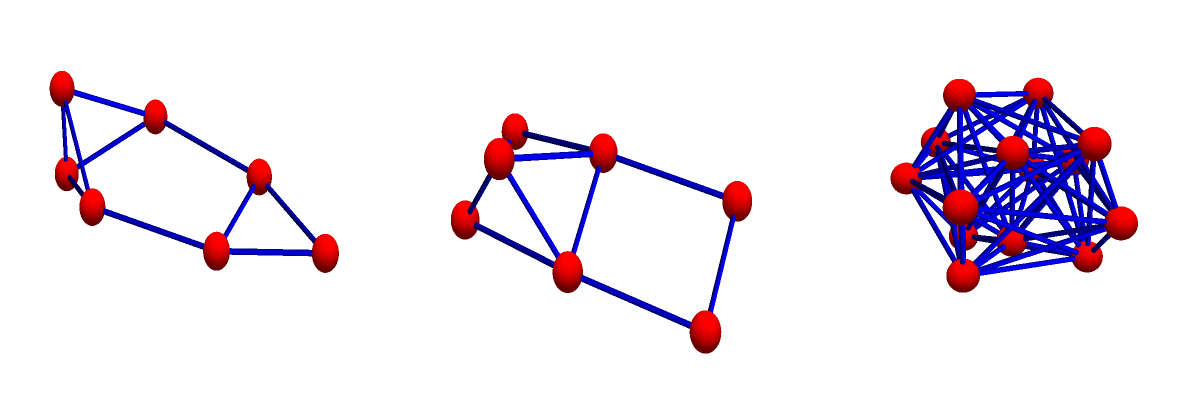
What happens if we look at the graphs generated by P₃. This is topologically also interesting even so we still have a trivial submonoid isomorphic to (N,0,+). But the Betti numbers of the Utility graph (P₃*P_3,) squared is already (1,0,0,16). This actually rises the question what happens in general with the cohomology when producing the join. The Betti numbers seem to multiply pretty nicely. Here are examples with random graphs. Of course we we multiply with a contractible graph, we get a contractible graph. Multpliplying with a sphere multiplies the homotopically nontrivial spheres producing predictable higher cohomology. Here are examples (the computer generated two random graphs, took the join, then computed the Betti vector of all three:)

{{1, 4}, {1,4 },{1,0,0,16}}             
{{2, 0, 0, 0}, {1, 1, 0}, {1, 0, 1, 0, 0, 0, 0}}
{{1, 0, 0}, {1, 1, 0}, {1, 0, 0, 0, 0, 0}}
{{1, 1, 0}, {1, 1, 0}, {1, 0, 0, 1, 0, 0}}
{{1, 1, 0}, {1, 3, 0}, {1, 0, 0, 3, 0, 0}}
{{1, 2, 0}, {1, 1, 0}, {1, 0, 0, 2, 0, 0}}
{{1, 1, 0, 0}, {1, 4, 0}, {1, 0, 0, 4, 0, 0, 0}}
{{1, 3, 0}, {1, 2, 0, 0}, {1, 0, 0, 6, 0, 0, 0}}
{{1, 2, 0, 0}, {1, 0, 1}, {1, 0, 0, 0, 2, 0, 0}}
{{1, 1, 1, 0}, {1, 0, 1}, {1, 0, 0, 0, 1, 1, 0}}

The situation seems the same as in the continuum because cohomology is just simplicial cohomology of a triangulation. It was Whitehead in 1954 who mentioned already that the join operation satisfies a Kuenneth type formula. (Whitehead says then “long known”). One actually can relate the cohomology of X x Y with X * Y Source. This seems also to be true in the discrete.
]