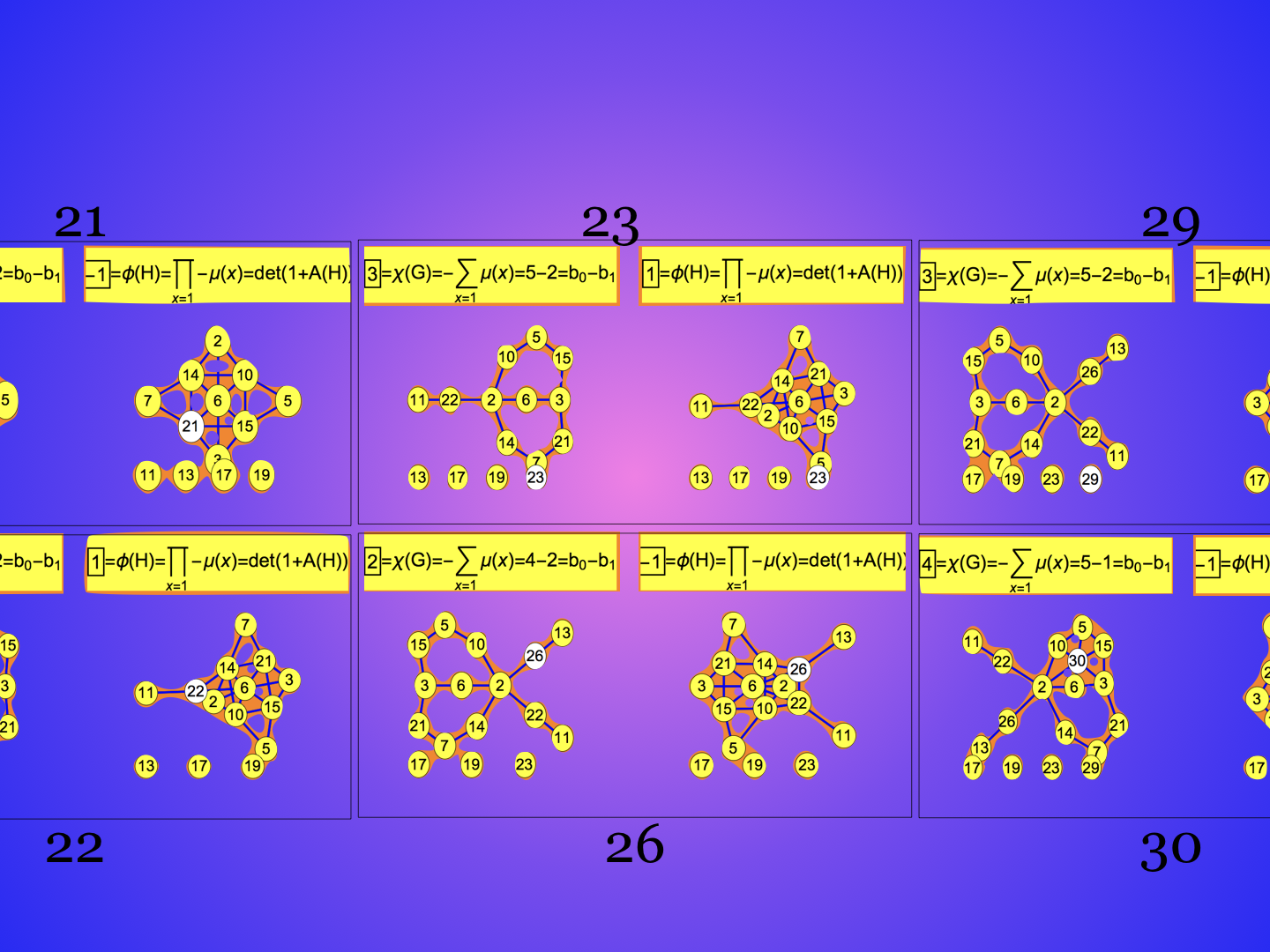
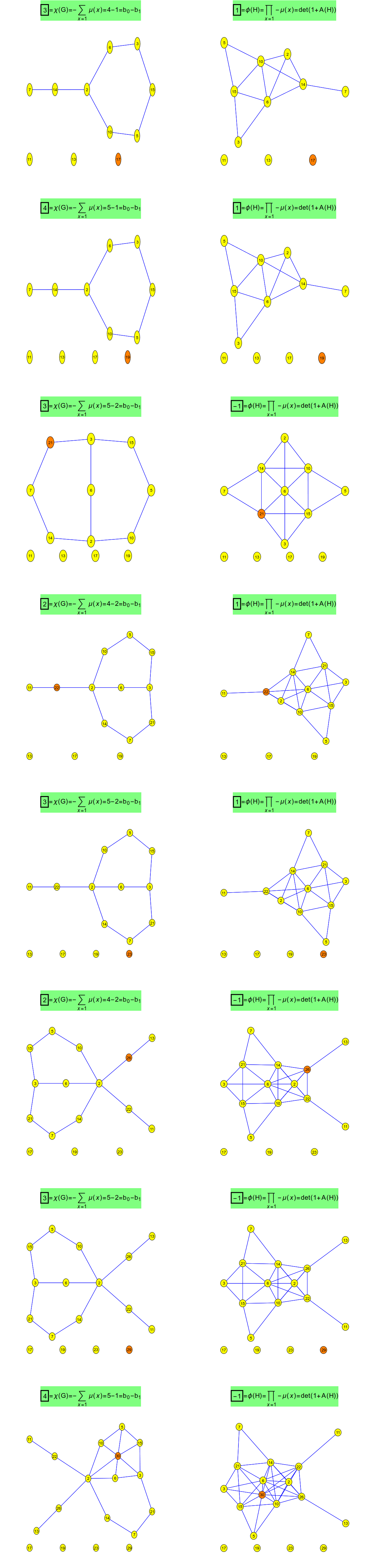
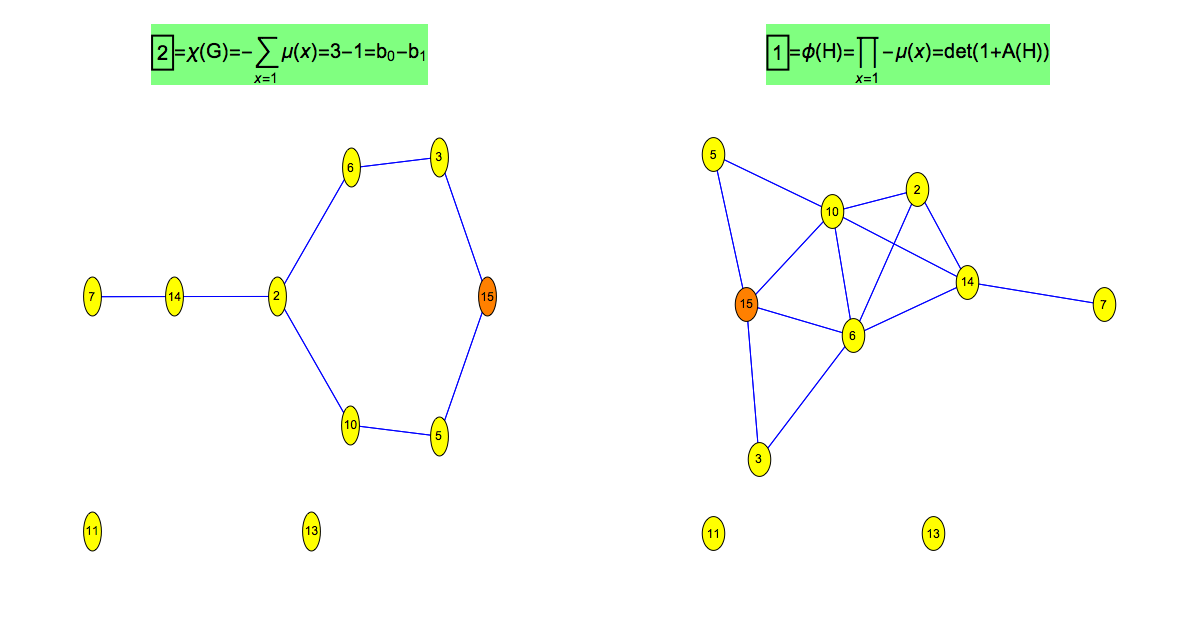
The following picture illustrates the Euler and Fredholm theme in the special case of the prime graphs introduced in the Counting and Cohomology paper. The story there only dealt with the Euler characteristic, an additive valuation (in the sense of Klain and Rota). Since then, the work on the Fredholm characteristic has made more progress and is now understood. The Fredholm characteristic is a multiplicative version of the Euler characteristic and a special value of the Bowen-Lanford zeta function, which is a Fredholm determinant counting up the parities of all one dimensional subgraphs of a graph and so a partition function or a path integral summing over all one-dimensional (not necessarily connected) “strings” in the geometry. In the context of primes and cohomology, we have on one side the Euler characteristic of the prime graph G (where two square free integers are connected if one divides the other), which is by Poincaré-Hopf the sum of indices, which are in this case the negative of the values of the Möbius function. Expressed as a Mertens function and writing the Euler characteristic in terms of Betti numbers the classical Riemann hypothesis is nicely tied to the cohomology of these prime graphs. On the multiplicative side, there is an other connection to Zeta functions, but the Bowen-Lanford zeta function, the Fredholm determinant of the adjacency matrix of the prime connection graph H (where two square-free integers (x,y) are connected if their GCD(x,y) is bigger than 1). We called this GCD graph in the experiments paper. The product of the negative of the Möbius functions is now the Fredholm characteristic. The picture is only understood when thinking about it geometrically: square free-integers are cells in a CW complex. Looking at the story using simplicial complexes alone does not work as the connection graph of the prime graph are much bigger. We have on the right hand side looked at the connection graph of the CW complex. Of course the Unimodularity theorem works also for the simplicial complex connection graph but then, we don’t have the multiplicative Poincaré-Hopf relation expressing the Fredholm characteristic as a product of the Poincaré-Hopf indices on the vertices of the graph. In the following table ω(x)=(-1)dim(x) where dim(x) is the dimension of the integer when treated as a simplex (square free integers are considered the cells in the CW complex).
| G(n) Prime graph | H(n) Prime connection graph |
| Additive picture | Multiplicative picture |
| Prime graphs | Prime connection graphs (GCD graphs) |
| Vertices are square free primes | Vertices are square free primes |
| Connected if one divides the other | Connected if there is nontrivial common divisor |
| Euler characteristic | Fredholm characteristic |
| χ(G) = ∑ ω(x) definition | φ(G) = ∏ ω(x) definition |
| Additive valuation | Multiplicative valuation |
| Poincaré-Hopf theorem | Fredholm Lemma |
| Euler-Poincaré relation | Unimodularity theorem |
| χ(G) = ∑ i(x) | φ(H) = ∏ i(x) |
| Introduced in “counting and cohomology”. | Introduced in “prime experiments” |
The first Poincaré-Hopf indices are (computed from the graph using the counting function) 1, 1, 1, -1, 1, -1, 1, 1, -1, -1, 1, 1, -1, -1, 1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1 The first Nonzero Moebius values starting with 2 are μ(x)=-i(x) -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, -1, 1, 1
In the picture, we also have included the Betti numbers (computed via Hodge as the kernel of Laplacians on k-forms). For these small graphs, there is no second cohomology appearing yet as no 2-spheres have appeared yet. The first 0-sphere has appeared at n=2*3, when attaching a 1-cell to the CW complex. The first 1-sphere has appeared at n=2*3*5, when attaching the unit disc of 30 to the CW complex. The first 2-sphere only appears at n=2*3*5*7=210.
And here are all the 255 paths which enter the Fredholm determinant of the prime connection graph for n=15. There are 128 paths with positive signature and 127 with negative signature. The unimodularity theorem assures that the difference is 1. This is special. For general graphs the Fredholm determinant is pretty arbitrary with a seemingly nice limiting distribution on Erdoes-Renyi spaces. So, here are all the paths. The blue ones are the paths with even signature, the green ones the paths with odd signature.
The Fredholm matrix 1+A of the graph has determinant 1. Here it is:
1 0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 1 0 0 0 1
And here is the prime graph and prime connection graph to n=15. Again, the left graph consists of all square free integers larger than 1 and smaller or equal to 15, where two are connected if one divides the other. The second graph is the graph with the same vertex set where two vertices are connected if they have a common divisor larger than 1. The graphs to the right were introduced in my prime experiment paper on page 49, where they were called GCD graphs (but were also non-square-free integers were included).