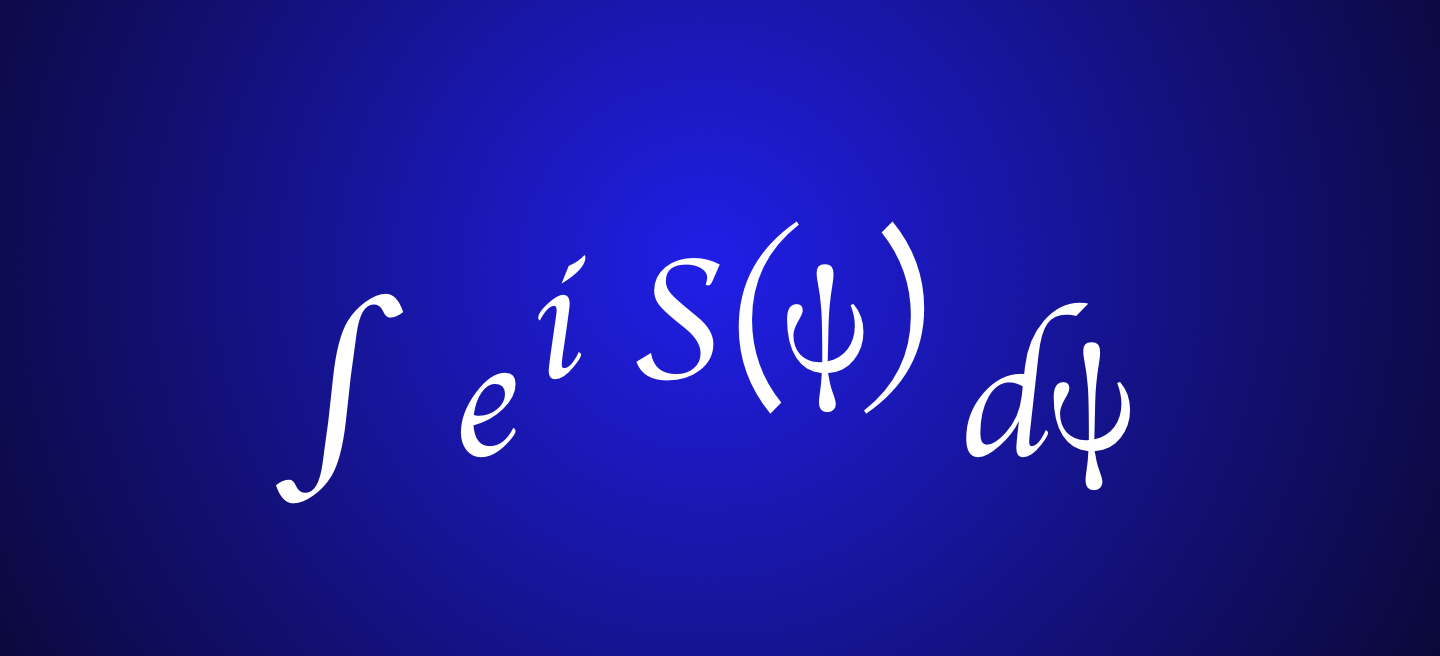Functional integrals on finite geometries

Baby quantum fields

Notions in quantum field theory can be considered on finite geometries. Functional integrals on finite geometries allow to perform “baby quantum field” computations. As a general rule, I will only be interested in such a computation if it should lead to some interesting numbers or to explicit functions. The basic idea of functional integration is to replace a particular computation with a natural probability space of cases and then sum. Information can then be obtained by taking derivatives. Like generating functions, Fourier transforms or other transforms, functional integration allows to express some quantities in a natural way. In a geometric setup, we hope that it helps to understand some topological invariants.

Motivation: Determinants

The simplest functional integral is a determinant. Given a $n \times n$ matrix A we can interpret a nonzero entry $|A(i,j)| = e^{B(i,j)}$ as a “transition energy” when transitioning from node i to node j. Now if $\gamma$ denotes a closed path visiting all nodes, define $H(\gamma)$ as the number of entries, where $A(i,j)$ is negative and $K(\gamma)$ the number of transpositions which build up the permutation $\gamma$ . Define now the action $S(\gamma)= H(\gamma) + K(\gamma) - i \sum_{k=1}^n B(\gamma(k),\gamma(k+1))$ . Summing over all possible paths gives the functional integral

${\rm det}(A) = \int e^{i S(\gamma)} d\gamma$ .

The integral is the counting measure on the symmetric group of all the permutations of n elements. When put this way, we see that the determinant is already a path integral.

Motivation: Fredholm Determinants

Given a simplicial complex G, we have looked at the connection Laplacian L, where L(x,y) =1 if two faces x,y intersect and L(x,y)=0 else. Given a one-dimensional closed path $\gamma$ in the connection Laplacian (allowing several connected components), one has an action $S(\gamma) = (-1)^{S(\gamma)} = \exp(i \pi S(\gamma))$ , where $S(\gamma)$ is the number of transpositions in the permutation attached to the path. Now, $\int \exp(i \pi S(\gamma)) \; d\mu(\gamma) = {\rm det}(L)$ . The unimodularity theorem showed that this “functional integral” is always either -1 or 1 so that L is unimodular such that its inverse g(x,y) is integer valued. The sum over all matrix entries g(x,y) is then the Euler characteristic. As Cramer’s formula shows that the matrix entries g(x,y) are determinants too, we see that in some sense, the Euler characteristic is already a functional integral.

Motivation: Characteristic function in probability theory

In probability theory, the characteristic function of a random variable X is defined as $\chi(t) = E[e^{i t X}]$ , where E[X] is the expectation of a random variable X on the probability space. It is the Fourier transform $\int_{R} f(x) e^{i t x} \; dx$ of the probability density function PDF f. Because the PDF of a sum of two independent random variables is a convolution of their probability densities, this corresponds to a product of the characteristic functions. We can definitely see the characteristic function as a functional integral. The action is the value of the random variable, the parameter t is some inverse temperature, the integral sums over all possible experiments doable in the laboratory. As in the case of determinants, there is absolutely no mystery what the functional integral is as in probability theory we start with a probability measure.

Motivation: Path integrals

The integral kernel $K(x,y)$ of $exp(-itH)$ , where $H=-\Delta_0/2 + V$ can formally be given as a functional integral (see e.g. Simon’s book on functional integration): given a polygonal path $\gamma_n=x_0, \dots, x_n$ approximating define $S(\gamma_n,t) = \sum_{k=0}^{n-1} |x_{k+1}-x_k|/2 (t/n)^{-1} - V(x_k) (t/n)$ which is an approximation of $S(\gamma) = \int_0^t \gamma'(s)^2/2 - V(\gamma(s)) \; ds$ . Since $(e^{i t (-\Delta/2)/n} e^{-i t V/n})^n$ has the kernel $\int e^{i S(\gamma_n,t)} d\mu$ , where $d\mu=dx_1 \dots dx_n (n/(2\pi it)^{3n/2}$ . Formally, there is therefore an expression $K(x,y,t) = \int e^{i S(\gamma)} \; d\mu$ for the integral kernel of $e^{-i t H}$ but it is known that this is only formal. One requires imaginary time to make sense of it. In the case of a finite geometry there is no problem however, the Laplacian $\Delta_0$ is the Kirchhoff Laplacian $L$ and the potential is $V$ . The operator is $H=L+V$ . Now, $\exp(i H)(i,j)$ is $\sum_{n=1}^{\infty} (i H)^n(i,j)/n!$ which is the sum over all paths connecting $i$ with $j$, where each path $\gamma$ has weight $1/|\gamma|!$ . Now, in the finite dimensional case, there is little need to expand the unitary evolution like that but it motivates functional integrals.

Motivation: index averaging

[This section was added April 26, 2017]. A theme we have used countless many times in this project is the principle

Averaging Poincaré-Hopf indices produces curvature.

Here are the three main papers, where the idea appears: 2012: Index Averaging, 2012: An index formula, 2014: Curvature from graph colorings. We can see these averaging results as path integrals. Integrating the discrete measures obtained from topological defects obtained from fields over a natural probability space of fields produces curvature. It is a rather classical theme in integral geometry. One of the pioneers in differential geometry was Blaschke, the doctor father of Chern, who used integral geometry extensively. As the above papers show, it is very natural in the case of general networks and more generally for simplicial complexes. Here is an other important principle which integral geometry provides (it appears as a remark in this paper and was influenced by work with Barry Tng, who wrote a senior thesis in integral geometry with me): integral geometry allows to measure length and more general quantities (k-volumes or curvatures) through expectation.

Functional integrals allow to bridge the continuum and discrete.

Here is a short summary: Nash embed a space like a Riemannian manifold in some linear or projective space E, then pick a measure on hyper-planes in E (this is particularly easy in the projective case). Use Crafton type formulas to define length. Take the Kolmogorov quotient to get a metric space. If the measure was discrete we have a discrete space, if the measure was smooth, we get a continuum (the Haar measure gives the Riemannian metric). But nobody tells us that we have to use discrete or smooth measures measure for averaging. We see that traditional geometry (discrete geometry on simplicial complexes for example, or continuum geometry on Riemannian manifolds for example) miss almost everything! A generic measure is neither continuous, nor discrete. Now what is nice about this setup that also notions like curvature, which in the Riemannian manifold case depend on sheaf theoretical tensor constructs, needing smoothness assumptions to have calculus work etc work without any calculus in general. Just define curvature as the expectation of indices. If the measure is supported on smooth Morse functions, then all have Poincaré-Hopf indices. The expectation of these indices is then the curvature of the strange space under consideration. We see that functional integration ideas allow to extend geometry to domains where nobody has even seen! Maybe there is interesting geometry between the discrete and continuum, but we don’t care. What is important is that there is unifying frame work in which quantized notions and continuum notions appear using the same mathematics. It also can explain why in many places where we see completely analogue theorems in the discrete and continuum. The quantum calculus versions are just much simpler.

Summing over waves

In quantum field theories or statistical mechanics, generalized notions of this idea appear. Given a probability measure $\mu$ on a space $\Omega$ of some fields and a real Lagrangian $H(\phi)$ one can look at the $Z(\psi) = \int_{\Omega} e^{i (H(\phi) + (\phi,\psi)} d\mu(\phi)$ . The number $Z(0)$ is the partition function. One is then interested in the k-point correlation functions $G(x_1,\dots,x_k) = \int_{\Omega} \phi(x_1) \dots \phi(x_k) e^{i H(\phi)} d\mu(\phi)/Z(0)$ . In the continuum, one has to find a natural measure on the space of all functions or to establish the integral through a limiting procedure. It seems that situations are in particular interesting, where the correlation functions relate to physics.

The case of finite geometries

On a finite geometry, functional integrals are objects from multi-variable calculus. They are just finite dimensional integrals. One possibility is to look at a simplicial complex G with n cells and all functions $\psi$ , taking values in the complex plane such that $\sum_x |\psi|_x^2=1$ . This is an integral over a $2n$ -sphere, for which there is a natural volume probability measure. The functions (fields) $\psi$ are here considered complex valued. One could look at real valued fields or fields taking values in some other group. The case of fields $\psi$ of L² norm 1 as in the case of finite dimensional Hilbert spaces this is a sphere.

Helmholtz case

Having looked at the Helmholtz dynamical system with Hamiltonian $H(\psi)$ defined on complex-valued functions $\psi$ one has a corresponding field theory. The evolution leaves invariant the sphere $S = \sum_x |\psi(x)|^2 = 1$ . The most natural measure $\mu$ is the rotationally symmetric measure. We can now look at the functional integrals like $Z(\beta)=\int_S e^{i \beta H(\phi)} \; d\mu(\phi)$ or $Z(\psi,\beta) = \int_S e^{i \beta H(\phi) + i (\phi,\psi)} \; d\mu(\phi)$ .

Partition function

The partition function $Z(\psi) = \int_S e^{i (\beta H(\phi,\beta) + (\psi(x),\phi(x))} \; d\mu(\phi)$ is a well defined integral as we integrate a smooth function over a finite dimensional sphere. One looks then at the correlation functions like the one-point functions $G(x) = \int_S \phi(x) \phi(y) e^{i H(\phi)} d\mu(\phi)/Z(0)$ , the two point functions $G(x,y) = \int_S \phi(x) \phi(y) e^{i H(\phi)} d\mu(\phi)/Z(0)$ etc. which is expressible through partial derivatives $G(x,y) = Z_{\psi(x) \psi(y)}(\psi)/Z(0)$ .

Questions

A basic question is therefore whether $Z(\psi,\beta)$ can be computed explicitly and whether there is some topological interpretation of the correlation functions, maybe in some limit. An other question is whether the contribution of the classical minima is the most important one. What happens in the case of the free energy Hamiltonian $F= \beta U - T S$ with $T=1-\beta$ , $U=\sum_{x,y} g(x,y) \psi(x) \overline{\psi}(y)$ and $S=-\sum_x p(x) \log(p(x))$ of the probability distribution given by $p=|\psi^2|$ .

First experiments

Given a random complex G, one can experiment with various different integrals. If $\psi$ is complex-valued and has total probability $1$ , one can integrate over a sphere. So far nothing interesting was seen. I’m not so much interested in random computations but hope that there will be some functional integrals which have some topological meaning. Advantage of experimenting over a general simplicial complex rather than a lattice (as in lattice gauge theory) is that one can experiment with various topologies and investigate the effect of the topology. I first experimented with $Z_G(\beta) = \int \exp(i \beta(\psi,g \psi)) d\mu(\psi)$ which is a complex-valued function of $\beta$ . The integral is then done numerically. Then we looked what happens if g(x,y) was changed, like with the connection Laplacian L’, the original Hodge Laplacian $L=(d+d^*)^2$ . Then we looked at the pseudo inverse of the Hodge Laplacian L. As L always has a kernel in the form of harmonic elements, it is not invertible but we can invert on the ortho-complement of the kernel. So far nothing interesting.