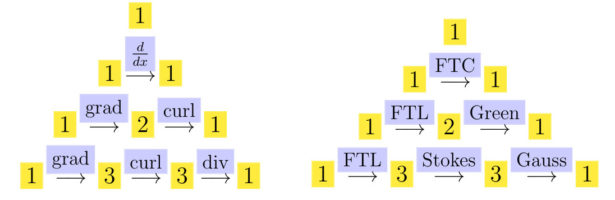
Geometries and Fields
quantum calculus

Geometries and Fields

Being in the process of wrapping up the latest summer calculus course, here are some thoughts about the frame work of calculus and more generally of classical field theories. It is an old theme for me which I think about often while teaching calculus. The question how to make calculus more natural and bring geometries and fields onto the same footing is a great theme and naturally leads to quantum calculus frame works. One can then have generalizations where one does not distinguish between geometries G and fields F any more.For example, if d is a linear nilpotent operator, G and F are both L^2 functions, then Stokes theorem becomes the simple identity (d^*G,F)=(G,dF), which is calculus in L^2. We just have to interpret d with an exterior derivative and its adjoint with the boundary. The operator d satisfying the nilpotency condition d^2=0 gives then a frame-work which looks like calculus and which leads to cohomology. For classical calculus, we have a huge asymmetry between geometries G and fields F. We can see G is a distribution supported on a lower dimensional geometry and F a smooth field. It is only if both objects are on the same footing that the pairing is perfect. One simple possibility is to see both G,H in the same Hilbert space (the most symmetric pair of spaces because the dual space is the space itself). Quantum mechanics therefore is the most natural frame work. There is however more to it. The question is how to symmetrize things in the classical real analysis frame work of differential forms and not just have an analogy. We try to write this here in a way which is as close as possible to what calculus textbooks do when describing the Cartan calculus of differential forms.

Pairing geometries and fields

Whether we look at calculus or at classical field theories in physics, there is always an interplay with geometries and fields. This is explained a bit in this handout [PDF] from a down to earth calculus course. In single variable calculus for example, we have the geometry [a,b], an interval and the field F given in the form f(x), which is a function. We pair the geometry G and the field F by integrating the field over the function. In multivariable calculus we have for example a surface G and a vector field F and the flux integral pairs these things up as (F,G). Geometries G and fields look very different in this set-up: the geometry is typically given as a parametrization r(u,v) from a region G in the plane to space and the field F is given as an object F=[P,Q,R], which is given by three functions in space. Stokes theorem gives the pairing between geometry and field. The flux integral of F through G is a number. Since the time when I was a student, I found the expositions we teach in multivariable calculus confusing at first. There is no beauty at first as in different dimensions, different frame works are at play. And there is a reason for that.It is that we cheat terribly. We “fuse” things together which actually should not be confused. The field F is actually a 2-form when we integrate over a surface. Every advanced calculus book tries to explains this, but this usually taps into multi-linear algebra by first defining the exterior algebra of differential forms. I tried again recently to explain the set-up without linear algebra. We write F=Pdydz+Qdzdx+Rdxdy and see expressions like dxdy as multi-linear maps mapping a pair of vectors (v,w) to a number. What dxdy does is take the upper minor of the Jacobean map dr (which is a 3 \times 2 matrix). This picture works then in general in any dimension dx_idx_j dx_k for example assigns to three vectors r_u,r_v,r_w the (i,j,k) minor of the matrix in which the vectors r_u,r_v,r_w are columns. This obviously untangles all the difficulties and solves the confusion.

Symmetrizing geometries and fields

One can see a geometry G as a smooth map from \mathbb{R}^d to some \mathbb{R}^n. The Riemannian metric on the image r(G) is then given by the matrix g =dr^T dr. This point of view of avoiding sheaf theoretical definitions of manifolds has some advantages, as it is extremely constructive. I have learned this point of view from Moser a great geometer and disliked abstraction for the sake of abstraction (he explicitly once pointed out in a functional analysis II course (which was actually a PDE course), that one actually can most of the time, when dealing with manifolds deal with surfaces embedded in Euclidean space instead. The Nash embedding theorem backs this claim up. Moser was a “down to earth mathematician” who is also known in the context of hard analysis like the Nash-Moser implicit function theorem. Bakonian and Descratian tasts oscillate in mathematics. We live now in a more Descartian area where generalization for the sake of generalization is fashion but thats ok. The two approaches fertilize each other. An article mentioning the tension between these two approaches is this BU talk from 2015.

Now lets look at an object like a 2- form F=A(x,y,z) dx dy in three dimensional space. It is a skew-symmetric bi-linear map which maps a pair of vectors v,w to a number. It is important NOT to see dxdy not as some sort of wishy-washy infinitesimal but as a symbol representing an anti-symmetric bilinear map. This can be implemented very concretely as follows in a Cauchy-Binet manner. Define F=\left[ \begin{matrix} 0 & A(x,y,z) & 0 \\ A(x,y,z) & 0 & 0 \end{matrix} \right] and use this as a map dr \to {\rm det}(F \cdot dr), where dr=\left[ \begin{matrix} (r_u)_1 & (r_v)_1 \\ (r_u)_2 & (r_v)_2 \\ (r_u)_3 & (r_v)_3 \end{matrix} \right] is the Jacobean matrix of the map r: G \subset \mathbb{R}^2 \to \mathbb{R}^3 parametrizing the surface. That is pretty cool as now, we can see a field F as the Jacobean of a map from \mathbb{R}^3 to $\mathbb{R}^2$. Fields so are a perfect {\bf dual} to the concept of a geometry. This point of view appeared in that handout [PDF] already for a slightly more advanced calculus course. For example, if F is just the adjoint of G, then the flux integral” \int_G F is \int_G det(dr^T dr) which is a Polyakov type action. But now, in general, the flux of F through G is the integral \int_G {\rm det}(F(r(x)) \cdot dr(x)) dx. In multivariable calculus, we write this as \int \int_G F(r(u,v)) \cdot r_u \times r_v \; du dv using the cross product, a notion which needs in higher dimensions to be defined via the exterior product, which typically requires to introduce tensors and skew symmetrization and formalisms. We can avoid a heavy dive into multi-linear algebra (we need determinants however) to define what a geometry and a field is and what the flux of the field through the geometry is. There are now various ways to define exterior derivatives in parallel to the boundary operation. If we look at the pair (G,F) as an inner product, we just make sure that (d^*G,F) = (G,dF) holds. This can be adopted for any linear operator d.

But it needs to be looked at differently as when we say G is a k-dimensional geometry, then d^*G should be a (k-1) dimensional geometry and if F is a k-field, then dF should be a (k+1)-field, which is now modeled as a map into a higher dimensional space. Furthermore, and this requires d to satisfy the relation d^2=0 also leading to cohomology. I had built such cohomologies more than 10 years ago in a Riemannian geometry frame work, but then graph theory hit me and all the stuff faded away. These papers are still sitting in my hard drive and I hope to get them out “pre-mortem” as it would be unbearable to have my hard-drives sold away and being erased by some computer gamer playing Battlefield V on the bits before filled before with a nice mathematical theory. Maybe I will write a bit more here soon once final exams are graded in the summer course.