Abstract for this post
Analysis had not been my favorite topic at first. The subject appeared to me quite technical and tedious even when sweetened like in analytic number theory. The Sine-Gordon topic and other rather concrete topics in dynamical systems theory changed that a bit and I ended up in the analysis group as a graduate student and at the end assisted in a book on calculus of variations. I would like to illustrate a bit why the Sine-Gordon topic is so exciting. In a second part, I would like to show why things have changed for me with the emergence of invertible Laplacians. The Sine-Gordon theme then becomes soft and relativistic, the reason being that we deal then even in non-compact situations with operators which have bounded, finite range inverses so that one can use the weak implicit function theorem to continue solutions from the linear to the non-linear realm. The connection analysis also makes the story more causal because the Green functions, the entries of the inverse of the Laplacian, are still defined locally and do not tap into space far away.
Sine-Gordon Variational Problems
If L be a linear operator like a Laplacian on a manifold, one can look at variational problems like which one can think of a as a sum of a kinetic and potential energy. Critical points
then satisfy
. The simplest potential one can think of is
, in which case one gets a Sine-Gordon type equation
. The name Sine-Gordon is a pun to Klein-Gordon, named after Oskar Klein and Walter Gordon who worked on that in 1926. Sine-Gordon had been studied even earlier than Klein-Gordon in the context of surfaces of constant negative curvature. It then resurfaced in 1939 when the Frenkel-Kontorova model appeared. Lets look at a few examples:
Nonlinear Pendulum
If , then we have the nonlinear pendulum
. By taking several copies, where
is now a vector one can get coupled systems like the double pendulum. This is an extremely interesting system because of the positive entropy problem: we measure positive Kolmogorov-Sinai entropy but are helpless still with proving it (or disproving it). I have been fascinated by the embarrassing mathematical failures we experience when dealing with such problems. Not that we have not tried (others even more than me), I tried for example to attack the double pendulum problem with plurisubharmonic analysis tricks. The pendulum itself is easily complexified and written as an analytic differential equation and even extended to other division algebras,but the problem is that the coupling does not seem to survive the complexification. It is a similar problem which I hit in 1986, when suggesting to use pluri-subharmonic techniques for the standard map. The “subharmonicity argument” gives the right lower bound but the analyticity argument does not work because the tori considered are not boundaries of polydiscs.
Frenkel-Kontorova
If is a discrete derivative we have the Frenkel-Kontorova system which leads to a nonlinear area preserving map
on
called the Chirikov standard map. Also here, similarly as for the double pendulum, the beautiful problem of positive Kolmogorov-Sinai entropy. Also here, the mathematical scandal is that one measures a lower entropy bound
but that one can not prove it. I had been fanatic about this problem from 1986 to 2000 and thrown essentially every possible math at it and terribly failed. The first attempt using pluri-subharmonicity by embedding the system into an analytic map on
was probably one of the best, but I tried also isospectral deformations (infinite dimensional Toda systems), spectral techniques from Schroedinger operators (positive Lyapunov exponents is linked to spectral properties), homogensiation techniques for subharmonic functions (a desperate but quite creative approach developed around 2000 when the subharmonic approach failed), finite Lax type approximations using Jensen type inequalities or phase space transport analysis (already in my junior thesis). Like for problems in elementary number theory, the problem is fascinating because it is easy to state and that the bounds are straightforward to verify numerically, but that the problem appears impossible to prove. It might even be wrong that the entropy is positive which is can be a reason to give up after 14 years of trying.
Sine-Gordon PDE
A third example is where the name Sine-Gordon is really used. It is the Sine-Gordon equation when . In that case, one obtains a beautiful partial differential equation which is integrable. It is famous because of breather solutions. Since a few years, I always assign the problem in multi-variable to verify that these breather functions satisfy the PDE (it is so hard that usually only one or two students manage to do the computations by hand and that most actually just use a computer algebra system to do the work). In graduate school, my colleague Jochen Denzler has worked on a subtle stability problem for breathers in a thesis. That work is published here. It needed a skillful analyst like Denzler to tackle such a perturbation problem. I admire this as I could never do such work myself. This type of heavy analytic technique is maybe one of the things which did initially not make analysis appear attractive to me. What makes analysis hard is that operators often are unbounded or that one has to tackle perturbations by approximation methods and heavy analytic machinery.
Coupled map lattices
The Sine Gordon frame work can also be considered in coupled map lattice situations. This is actually a quite general frame work, where one considers a graph G and at each node runs a dynamical system, which can be a map or a differential equation. One can then study what happens if one starts to couple the independent systems. We looked in this paper with Arne Jakobsen (whom I had met in Danemark at the Hillerod Conference) at some general construction in this domain. At Caltech, I also looked at coupled standard maps which emerged when looking at extremization problems of Wilson type. The paper was called “Nonlinear dynamics from the Wilson Lagrangian”. It is quite a neat variational problem to mazimize the functional on some space of operators, where m is a mass parameter. This naturally leads in the simplest case to Henon type cubic symplectic maps and in higher dimensions to coupled map lattices where one can prove the existence of bounded solutions using the anti-integrable limit of Aubry. Here are some figures from coupled maps. The pictures were made in 1996 still on a Next computer with Mathematica and the code is from then:

And here is the Mathematica code written then in 1996:
Wave[m_,n_,a_,Mass_,c_]:=Module[{},s={};mm=Round[m/2];
K[t_]:=Table[N[-a*(t[[Mod[i-2,m]+1]]+t[[Mod[i,m]+1]]+4*t[[i]])
-(4-3Mass)*t[[i]]-t[[i]]^3],{i,m}];
u=Table[If[Abs[k-mm]<100,c*Random[],0],{k,m}];v=RotateLeft[u];
Do[{u,v}={K[u]-v,u};s=Append[s,u],{k,n}];
ListDensityPlot[Re[s],Mesh->False,ColorFunction->Hue,
PlotRange->{-0.3,0.3}]];
S=Wave[400,400,-0.35,1.19,0.4]
Here is a new rendering with 800 coupled maps. One can see some interesting soliton type interactions. This is a very non-trivial problem. Already if we take one node, we have the Henon map which is an extremely interesting system featuring a lot of structure despite its simplicity.
Discrete PDEs
Finally one can mention systems where
is a Laplacian on a graph or finite abstract simplicial complex. A natural case for example is when
is the Hodge Laplacian defined by an exterior derivative d. One then has a natural perturbation problem in which the Laplace equation
is the base point with Harmonic k-forms as solution in each k-form sector. Again here, like in the previously stated examples, the perturbation theory is non-trivial because one has a non-invertible Hessian matrix (linearization). If the graph is the integers
, then one has the Frenkel-Kontorova model and the perturbation problem is a prototype KAM problem which features interesting transitions from integrability to chaos. The large c case has simple solutions from the variational point of view because of the Aubry-Anti integrable limit. Then there are Aubry-Mather transitions and as already mentioned the question whether there is a transition to positive metric entropy. One can also extend this to the Klein-Gordon theme by replacing
with a d’Alembert operator like
leading in the finite graph case already to complicated non-linear ODE’s. See also this document on discrete PDEs on graphs from a HCRP project from 2016. Some pictures of Sin-gordon systems on graphs can be seen here. These are ordinary differential equations
where
is a scalar function on the nodes of a graph and
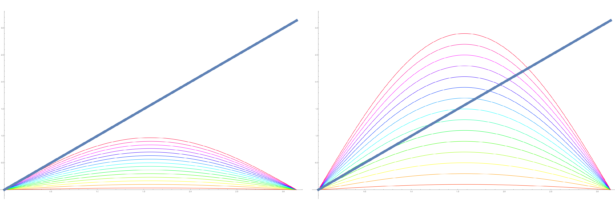
is the Kirchhoff Laplacian of the graph. Here is the picture seen there done in the first interesting case, where the graph has two connected nodes. These are two coupled penduli. One of the original goals of the project with Annie Rak was also to establish integrability for these type of Sin-Gordon problems. We ended up doing more advection on graphs in the end.

Linearization: Almost Mathieu case
Each variational problem solution describes critical points of a functional. The second derivative, the Hessian is also of great interest. It linearizes the system along the critical point. Already in the simplest cases, this is hard. For the Frenkel-Kontorova model for example, one already is led to difficult spectral problems. When looking at the spectral problem on a KAM torus one gets already operators similar to almost Mathieu operators. The later is the case when the dynamical system is the irrational rotation from the c=0 case. At Caltech, I started once to work with Yoram Last on the spectral problem appearing in Standard maps, especially for the Birkhoff periodic orbits, where finite linear algebra can be used. Last has developed nice powerful perturbation results in order to analyze the almost Mathiew operator We both got tied up in other projects however.

Hard perturbation problems
The spectral theory of Hessians of Sin-Gordon variational problems is highly unexplored. The only thing which is clear is that it is not-easy due to the fact that we have at c=0 a non-invertible situation. This non-invertability requires hard implicit function theorems, tough analysis. In physics in general, the non-invertibility of the Laplacians is the major source for technical difficulties. The Green functions are unbounded and singular, one has to introduce retarded potentials, renormalization and all kind of difficult techniques to understand when one switches on the non-linear parameter c. Usually, even in ODE situation, already the problem of stability of solutions is difficult. In PDE situations it can be brutal. Hard implicit function theorems like the Nash-Moser theorem help to make the topic appear easier.
Hacks
Before coming the connection Laplacians, let us mention an other problem with the usual Laplacians we have in analysis: the are long range in the sense that the Green function entries can tap into parts of space which is in a relativistic setup unacceptable. This is even the case in finite dimensional situations. If is the Laplacian, then the pseudo inverse
is non-local in the sense that even for arbitrary far apart pairs (x,y) we have g(x,y) entries which are not zero. The wave equation
is local in the sense that the function value of
for
does not influence the value. When looking at Fourier solutions one uses eigenfunction expansions dealing with the entire initial condition. When looking at the wave equation
, where
is the Hodge Laplacian, the explicit d’Alembert solution is
can be written down explicitly as D is a concrete self-adjoint matrix defined by the graph. But already with zero initial velocity, the solution
of the wave equation appears non-local as the Taylor expansion of
involves arbitrary large powers of the local Dirac operator
. Since the non-invertibility of the Laplacian is difficult for perturbation questions, I was so excited to find a Laplacian which always has a bounded inverse and is still natural. I felt this to be so important that I left other very interesting research and focused on that. Here is a presentation from 2017.
Connection Laplacians
If G is a simplicial complex which has the property that there is a bound on the degree of the connection graph in which the sets of G are the vertices and two points are connected if the sets intersect. In that case there is a bound on the inverse g(x,y) of the connection Laplacian L(x,y) and g(x,y)=0 if x and y are far away. Now, we can look at the Sine-Gordon problem we have a perturbation problem which in the case
has waves as solutions. Now, if
is a discrete time derivative then for small
, the operator
is invertible and by the standard implicit function theorem, these solutions persist also for small c. It is an elementary fact from the implicit function theorem that if L is an invertible operator then L u = c sin(u) has only the solution u=0 for small u. One can dub this in a fancy way and say the vacuum is stable. The simplest example is if G is a single point. In that case L u = u is the multiplication by 1 and the critical points satisfy u= c sin(u). For small c (actually for
, there is only one solution to u = c sin(u), which is the vacuum solution u=0. For
however, there are two solutions. In dynamical systems jargon, one speaks of a bifurcation. For more complicated networks, the bifurcation story becomes much more interesting. The reason is that for
there are
non-zero solutions with values in
. Also any of these solutions are stable by the anti-integrable limit. Write the problem as
, which for
has any $\latex \{0,\pi\}$-valued function
as a solution. Also here, by the weak implicit function theorem, the solutions survive for small
. All this also works for infinite networks, the reason being that there is an explicit bound on the inverse of the operator L or the multiplication operator with
.
Mass gap
The reason for the bounded inverse of the connection Laplacian is very general. Here is a paper explaining the energy theorem in the simplest case. It is clear from the explicit formulas for the inverse that the inverse entries
only depend on a neighborhood of x and that therefore, even for infinite networks the operator g stays bounded. There is a mass gap as a physicist would say. Such mass gaps are conjectured in Yang-Mills theories. Here it is the case that even if the operators take values in division algebras, the bound of the Green function remains. It is of course not a solution to the Yang-Mills problem in the Millenium problems but it bypasses the difficulty by entirely by having a different frame work, where the operators are always invertible. Now this could be interesting in physics: assume for example that the simplicial complex G has as atoms small Planck sized space units and that G is the Whitney complex of the graph in which two such sets intersect if they intersect. This set-up can also be done in the non-standard mathematics setup IST of Nelson where one knows that there is always a finite set which contains all standard element of say a manifold. It defines then a abstract finite simplicial complex. Yes, it is non-standard but one can use finite mathematics to study it. In order to have an explicit bound on the Laplacian, one has to establish a finite upper bound on the number of neighbors of a point. This can be justified too. In any case, if we take such a network, then depending on the maximal vertex degree there is an explicit interval [-a,a] free from spectrum of L. Now, if we think of L as some sort of d’Alembert operator, then
is a non-linear wave type equation. Alternatively one can look as before at
where
is an additional mass parameter and
a discrete second derivative. We have then Dirac type solutions to
given in the form
, where
and
and
are adapted trig functions as
are discrete time derivatives (calculus can be deformed to quantum calculus). Interestingly, these waves survive also if the non-linearity
is switched on. We know also that something interesting must go on when c is getting larger. At some points, the continuation of the waves are no more the only stable solutions.
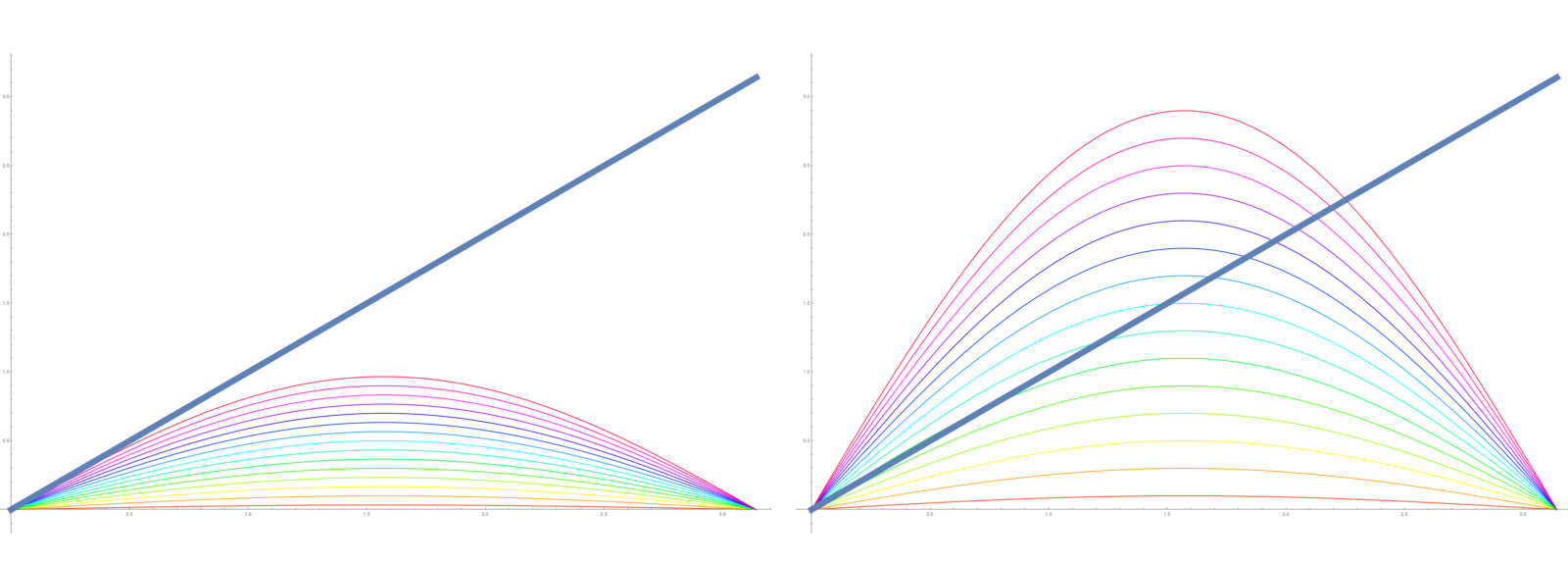
Phase transition
For large c, there are many non-trivial solutions to . This is called the Aubry anti-integrable limit. The solutions are Bernoulli system in a Frenkel-Kontorova set-up. For
, we have an equivalent problem
which allows solutions
taking values in
. So, we see that there must be some sort of phase transition, where wave type solutions morph to complicated solutions. How that transition looks like should be investigated more. For finite networks G, one has even a chance to see the entire bifurcation diagram. Best is probably to continue the solutions coming from
and see what happens with them when they disappear. I studied this anti-integrable limit in this paper from 1996 for the standard map. Aubry’s idea gives lots of horse shoes (invariant Bernoulli systems) for large c. There are infinitely many but they are countable so that they have measure zero. The anti-integrable limit does not establish positive metric entropy for large c, only positive topological entropy and the point of my paper was to give explicit lower bounds on the topological entropy. The Standard map is a variational problem featuring a lot of intersecting different phase transitions. One has the KAM stability regime, the Aubry-Mather phenomenon, the Aubry anti-integrability solutions. From a measure theoretical point of view one know much less (this is ergodic theory). KAM establishes for small c regions of positive measure on which the map is still integrable. Thats all we know. We do not know the entropy, we do not know ergodic components of positive measure (an equivalent problem to positive entropy by Pesin theory).