Homotopy Manifolds

The problem of discretization

It is a question which probably was pondered first by philosophers like Democrit or Archimedes. What is the nature of space? It is made of discrete stuff or is it a true continuum? As Plato already noted, such questions border to being pointless as we live in a cave and only see the shadows. Indeed, we can process a finite amount of data only and hardly ever will understand the true nature of space. Great philosophers like Kant made a bit a fool of themselves by trying to explore such questions by thought only. (The case of Kant probably indicate best that in order to talk about space and time, a modern thinker needs a serious background in mathematics and physics. Otherwise, one can not interpret the shadows in Plato’s cave at all). What matters if we explore our existence is what we can measure and not what we think is beautiful or elegant. And even if space should be discrete with a fundamental minimal length of say meters, there would be maybe vertices to be seen in this graph, a pointless endeavor, given that we estimate the number of particles in the accessible universe to be of the order . We can say with certainty that we have no chance to see space in its completeness, simply also because information travels with finite speed. If some advanced intelligence (or deity) would be able to alter fundamentally the structure of space somewhere in an other galaxy, we would know about this modification only much later. It is natural and in the human nature to dismiss the continuum because it is inaccessible. Democrit did it for matter. He turned out to be right, but at his time, there had been absolutely no evidence at all that this is the case (Democrit probably looked at sand and discovered small quartz parts which could no more be separated and extrapolated. A bold but actually very stupid thing from a modern point of view. One must give Democrit some credit however as he was the first to extrapolate in such a foolish way. He was not alone. Archimedes estimated the number of sand grains in the Sand reckoner paper.). Only thousands of years later, quantum mechanics indicated that matter indeed is discrete but that is not the last word as we have no idea yet what is beyond fundamental constituents like electrons or quarks.

[ By the way, speculation is always cheap. We see that today with thousands of models of space and time exist. Every kid can speculate. I remember that when I was in middle school, and learned about planets and atoms I wondered whether the atoms are planetary systems (people living on electrons). It is an analogy which is natural as both deal with objects rotating around each other. It is of course a foolish analogy which probably is at some point done by any kid learning that stuff and is done because in both cases we have something turning around something else. If a new discovery appears like the Muon anomaly, within a few days, we have dozens of new theories which explains this perfectly well and prove that the Standard model needs to be modified. The same time of the announcement there was a paper published which revises the magnetic moment anomaly of quantum field theory and puts the anomaly into the range of measurement errors. Everybody can guess and build theories. It would be possible these days to have a computer empored with AI software to randomly generate physical theories which are reasonable and even give correct predictions of new phenomena. Maybe the 10 million’th guess would be correct. Is this an achievement? No, it is pure luck. I can predict the license plate of the next car I will see by making 10 million guesses. My lucky hit does not prove that I can predict it. Maybe we should for any scientific prediction which turned out to be wrong reduce the reputation of the scientist who did it. Even if a theory is good and accurate it can still be stupid. There is the famous story told by Dirac who had a wonderful theory which fitted data extremely well. Postdocs and graduate students had been lined up for the project. Dirac went to Fermi and told him about it. Fermi asked: how many parameters did you use? Dirac replied: 5. Fermi immediately dismissed the model and told that with 5 parameters he can fit an elephant. Fermi had been right. It is not only the elegance which can fool us, it can also the complexity of a complicated model fitting very well which can fool us. The epicycle theory of our ancestors was very good, it was complicated, a very good fit but it was only a Fourier approximation of the elliptic motion and the elliptic motion also turned out to be a a dream idealization given that all planets interact. Newton’s model which explained the true nature turned out to be a naive simplification too, given the relativistic nature of space and general relativity again is just a model which clashes badly with some quantum mechanical considerations. ]

The Pythagoreans resisted the notion of the continuum at first for esoteric reasons but they had to accept eventually that harmony can also be found beyond the integers and fractions. The rise of computer science and numerical method as well as the difficulties with singularities and infinities in quantum field theories naturally pointed again and again to discrete models. This turned out to be useful also, like when developing numerical schemes. A famous one which is covered in the heavy Gravity book by The trivial observation that we can process only a finite amount of data makes us do the Democrit speculation. We all the time look at finite models. If we look at tight-binding approximations of Schroedinger operators, lattice gauge theories, spear-headed by work like Regge’s, percolation models, triangulations of surfaces, numerical methods for partial differential equations like partial difference equations, or particle in cell methods (PIC). In geometry, manifolds are triangulated. In computer games, it is of fundamental importance to capture the essence of space effectively so that GPU’s can process millions of triangles a few dozen times per second.There are only a finite amount of triangles we can build but still, modern computer games look almost real.

There is an obvious problem with discrete models which everybody is aware of: natural symmetries are broken. Rotational symmetry for example is absent as the rotation group is a Lie group. Mathematicians have tried all kind of things: include randomness, use quasiperiodic tilings or simply ignore the issue and try to do computations on a lattice (the above mentioned Muon anomaly has been explained by such lattice gauge field theories). Usually, we discretize partial differential equations with adapted meshes and refine the mesh near interesting places. An other tool (which I know from my wife who worked in her thesis on Supernovae explosion simulations with particle in cell methods on Cray computers) is the PIC. The motion of particles in that model are governed by laws honoring rotational symmetry but the choice of the cells does not. Still, the PIC is a PDE method which is closest to reality which also features fundamental particles. The last two months, triggered by a topic in graph theory, I pondered the question again and played with various definitions of discrete manifolds which are more robust and able to feature symmetries. It does not tap into the difficult notion of triangulation. On a fundamental level, it allows even to have combinatorial rotationally symmetric situations (using non-standard analysis IST) but non-standard analysis can be ignored also. It is all just combinatorics and graph theory. Here is a video memo documenting a bit my struggles this spring. I find talking about it and posting it an effective way not to forget. I have dozens of unfinished projects on every of which I could easily spend the rest of my scientific life on. Time is short and I have to work hard to get some of them to see the light. So, here is the presentation which also allowed me to explore my inner child and pop up some spheres (Spheres are manifolds which pop when a point is removed!)

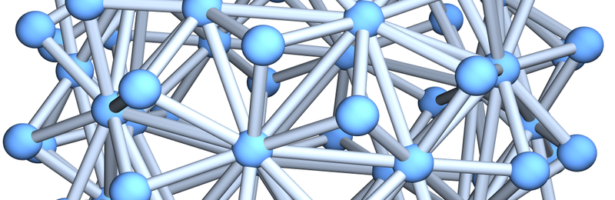
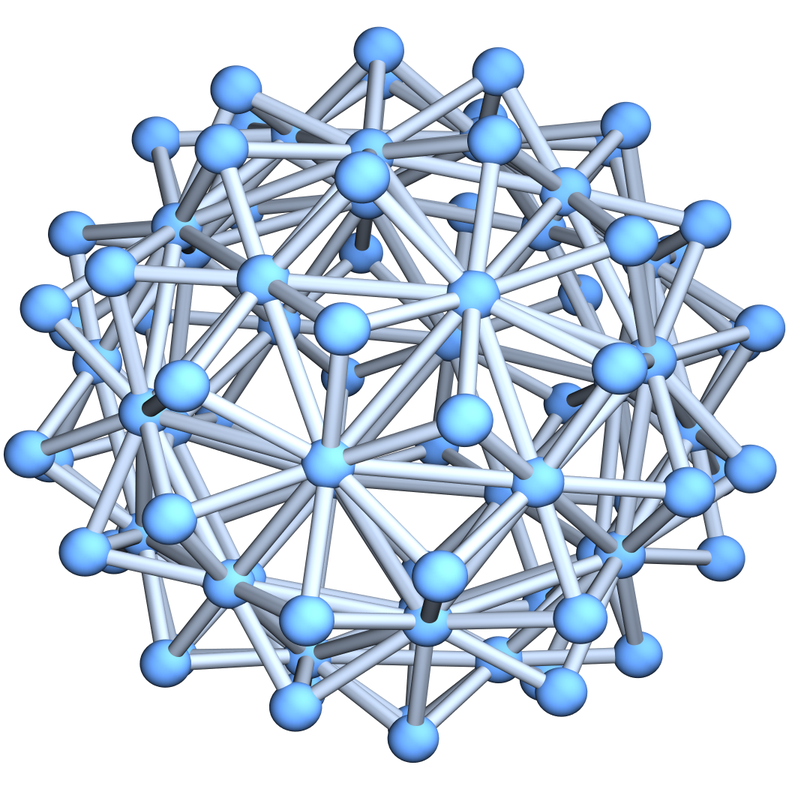
The following notion has come out after pondering various definitions. What counts is not only elegance in the definition, it is whether one can prove theorems with that notion. There are various definitions which are natural but which do not allow to prove theorems. For me it is pivotal for example that if one has a function f on such a d-manifold, the level surface { f=c } is a (d-1) manifold. We want in particular that spheres of small radius are (d-1) spheres. The later is actually on the smallest distance level not achievable and that is what we give up. We want every unit sphere to be either a (d-1) sphere or then to be contractible. The later is absolutely crucial. If we look at space and take a radius smaller than the Planck constant, then it could happen that the unit sphere is no more a sphere but contractible. But we do not have to go into the quantum worlds: very natural models of space like floating point arithmetic on a computer or triangulations of 2-manifolds are not discrete 2-manifolds for example because we have 3-simplices in the system. Already very natural polytopes like the equidnahedron come in this form. (The figure at the beginning is that polyhedron). There are unit spheres in that space which are contractible. (The outer spikes have unit spheres which are triangles). This is very typical in data models. Take any finite data and organize them, then build a complex in which things are connected below some distance threshold. Such simplicial complexes are in general messy.

Definition of Homotopy manifolds:

Here is the definition which emerged after a considerable amount of thought. I predict it is a definition which will prevail in the sense that it leads to theorems which can be proven with relatively low effort. The definition is close to the inductive definition of d-manifold which I have been using since maybe 9 years but which traces back to notions put forward by Evako in the 1990ies. There is an alternative, more analytic approach of Forman developed at about the same time which is equivalent by a discrete theorem of Reeb characterizing spheres:

The definition is inductive: the empty graph is a sphere, the -point graph is contractible. A graph is contractible if and are both contractible. A graph is a homotopy d-manifold if for all , the unit sphere is a homotopy (d-1)-sphere or contractible and any homotopy contraction step which does not destroy any other (d-1)-sphere can only preserve the homotopy type of any other unit sphere or produce new homotopy (d-1) sphere from a contractible one. We call these safe homotopy reductions. A homotopy d-sphere is a non-contractible homotopy d-manifold such that after some possible safe homotopy reductions which do not change the homotopy type of the graph, there is a vertex v such that G-v is contractible.

The definition is reasonable because we can almost without effort (see this talk) show that a d-sphere has Euler characteristic which follows also right from the definition for homotopy d-spheres.

Remarks: this definition emerged after trying out many other definitions. This entire spring, I did write little but think, mostly during 2-3 hour daily excursions running and walking. At the moment I believe, the above definition is good. Details are important. We want to capture also the dimension nature of space in the sense that if we look at a unit sphere, then it becomes contractible after removing a substantial part of it and that the unit sphere has a (d-1) dimensional nature. Homotopy d-manifolds can have huge maximal dimension. This is typically happening when looking at triangulations of space. Take a surface for example and refine a triangle by placing a new vertex in the middle, connecting it to all three vertices. This produces a 3-dimensional cell. Hardly anything we want to have in topology as a surface is 2 dimensional. Still, if we scan an object and build a point cloud we have usually a total mess in the point cloud. Numerical methods allow us to reduce this and simplify the point cloud to get a nice triangulation but this is harder and harder in higher dimensions. The famous Hauptvermuting illustrates the struggle with triangulations. It is a very hard thing in higher dimensions. Now, if we want to prove theorems, we do not want to deal with such complexities. We want simplicity. The nice thing is that we take a dense enough point cloud representing a Riemannian d-manifold, then this is a homotopy d-manifold already. This is very robust. The balloons which were popped up in the movie are 2-spheres. But of course they are not 2-dimensional surfaces. They have thickness and are made of a complicated mesh of polymers which are so well entangled that air molecules can not escape. But they are not three dimensional in the sense that there is no point inside which has a unit sphere which is a 2-dimensional sphere. The rubber entanglement is so thin that removing one either does nothing (the unit sphere is still contractible) or then a 1-sphere in which case the balloon pops! See this twitter post.

Examples of homotopy manifolds:

Examples: the complete graphs are homotopy manifolds. a d-manifold with or without boundary is a homotopy d-manifold. A wheel graph for example is a homotopy 2-manifold. There are no safe homotopy reductions any more possible as it would destroy the center unit sphere which is a cyclic graph. Without that safe guard to preserve already produced unit spheres which are spheres, we could collapse the wheel graph to a point. It would be pointless as all contractible spaces like all balls (independent of dimension) would all be just points. This is completely unacceptable for a topologist who insist on having a notion of dimension.