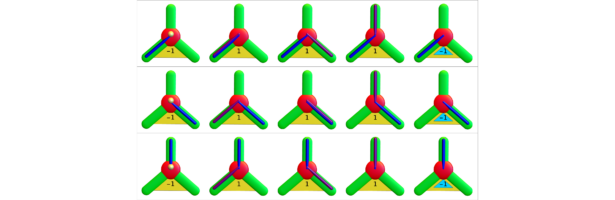
Quadratic Characteristics
The elements of Euclid of Byrne (internet archive) are a nice example also in how to illustrate mathematics. The tools to illustrate mathematics have multiplied since Byrne’s time. Yesterday, I wanted to visualize the identity w(B(x))=w(U(x))-w(S(x)) for quadratic (Wu) characteristic which comes after linear (Euler) characteristic. In the video, the …