| Abstract: If $L$ is the connection operator of a complex and $J$ is the checkerboard matrix $J(x,y)=\omega(x) \omega(y)$, where $\omega(x)=(-x)^{{\rm dim}(x)}$, we note that $LJ$ has then the Perron Frobenius eigenvector $v$ given by Wu-intersection numbers $v(x) = \omega(x) \omega(G,\{ x \})$ as components. The matrix $LJ$ has only one non-zero eigenvalue $\omega(G)= tr(LJ)$. We also have $\omega(G) |G| = tr(JLJ)$ where $JLJ$ is symmetric but conjugated to $LJ$. Wu characteristic is therefore spectrally defined through a symmetric matrix but as $JLJ$ has rank one, this is not a good “Hamiltonian”. But we still don’t know whether $\omega(G)$ can be obtained from the spectrum of $L$. |

|
 |
| Perron | Frobenius |
In this post, I want to point out a connection of Wu characteristic with Perron-Frobenius. It is not deep at all but interesting and illustrates how Wu characteristic is natural. Perron-Frobenius is a key idea in mathematics. It is crucial for example to understand Markov processes, Chaos or Page rank. Indeed, the “billion dollar vector” of Brin and Page is a Perron-Frobenius vector. See a (handout of 2011 [PDF]). The idea is tangentially also involved here. First of all, since the connection Laplacian L has non-negative entries and is invertible, there must be a positive eigenvalue. I had tried first to prove directly that L never can be positive definite if the complex has positive dimension but this only emverged as a consequence of e more detailed analysis showing that the number of negative eigenvalues matches the number of odd dimensional simplices in the complex so that can hear the Euler characteristic $\chi(G) = \sum_{x \in G} \omega(x)$ of a simplicial complex $G$. I also experimentally saw that the Wu characteristic $\omega(G) =\sum_{x,y \in G} \omega(x) \omega(y)$ coincides for pairs of L- isospectral complexes found so far. This prompted the question whether one can hear the Wu characteristic using $L$. I don’t know this yet. But it is already possible to express Wu characteristic as an eigenvalue of a symmetric matrix $K$. We want to see here that this matrix $K$ has an explicitly given “Perron-Frobenius” eigenvector whose eigenvalue is the Wu characteristic.
I had actually started to look at the operator $L$ originally because ${\rm tr}(L J)$ is the Wu characteristic, where $J(x,y) = \omega(x) \omega(y)$. The observation done early 2016 that $L$ is always invertible lead a bit away from Wu characteristic. But both notions are central in a calculus, where not the simplices, but pairs of intersecting simplices are the focus. The case where functions on simplices are involved is the classical differential form calculus taught calculus. The calculus of Wu characteristic and its cohomology has no continuum analogue so far.
In quantum mechanics, one could interpret $J$ as a density matrix and $tr(L J)$ as the expectation of $L$ in that state. Actually $J = p^T p$ is in a pure state given by the vector $x \to p(x)=(-1)^{{\rm dim}(x)}$. In Dirac notation, this is $| p \rangle \langle p |$. The operator $L J$ is not symmetric. Here is an observation: define the matrix $P=J/\sqrt{n}$, where $|G|=n$ is the number of simplices in $G$. The matrix $P$ is symmetric, so that also $K=P L P = P^T L P$ is symmetric. This matrix has the eigenvector $p(x)=\omega(x)$ with eigenvalue $\omega$. As $K$ has rank $1$ it should be dismissed as a Hamiltonian.
|
The symmetric matrix $K$ has exactly one non-zero eigenvalue: the Wu characteristic. Its eigenvector is the vector $p$. |
Proof. The matrix $P$ has the eigenvector $p$ with eigenvalue $1/\sqrt{n}$ so that $P L P p = P L p/\sqrt{n} = J L p/n$. Since $J$ has rank $1$, also $J L$ has maximally rank $1$. But ${\rm tr}(J L p)/n = n (p L p)/n = p L p = \omega$. As we have the same eigenvectors and both matrices $J,K$ are symmetric, they are a multiple of each other. We have $K = \omega J/n$.
So, the matrix $K=PLP$ is really not that interesting. However, we could also look at $L J + J L$ which is also symmetric but it has exactly two nonzero eigenvalues.
What is the eigenvector of the matrix $L J$ to the single non-zero eigenvalue $\omega(G)$ it has? Note that the matrix $J L$ is easier as it has the eigenvector $p$. The situation is a bit like for Markov operators, where the operator $M$ as a trivial constant eigenvector with dominant eigenvector but where the transpose $M^T$ is interesting. The eigenvalues of M and $M^T$ are the same but the eigenvectors not.
Since the situation is so close to a Perron-Frobenius situation with one dominant eigenvalue, we can say that the Wu characteristic is essentially a Perron-Frobenius eigenvalue of $L J$ (we abuse here a bit the language as $LJ$ is not a non-negative matrix but only conjugated to a non-negative matrix. In some sense, we are only at the boundary of the Perron-Frobenius story).
Given two simplicial complexes $G,H$ we called $\omega(G,H)$ the Wu intersection number. A special case is $\omega(G,G)$ which as a self-intersection number is the Wu characteristic itself. We can now see that the Perron-Frobenius vector is built up by such intersection numbers.
|
The matrix $LJ$ has exactly one non-zero eigenvalue: it is the Wu characteristic. Its Perron-Frobenius eigenvector is $v(x) = \omega(x) \omega(G,\{x\})$. |
For example, for a star graph G with n-1 rays, the eigenvector has entries n-1 at the center and n-2 on the edges and zero else. In the particular case n=5, we have $G=\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1\},\{2\},\{3\}, \{4\}, \{5\}\}$. Now
$ L=\left[\begin{array}{ccccccccc}
1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 0 \\
1 & 1 & 1 & 1 & 1 & 0 & 0 & 1 & 0 \\
1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\
1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 \\
\end{array} \right] $
The Green’s function matrix, the inverse is
$ g=L^{-1} = \left[
\begin{array}{ccccccccc}
-1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 & 1 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & -1 & 1 & 0 & 0 & 0 & 1 \\
1 & 1 & 1 & 1 & -3 & -1 & -1 & -1 & -1 \\
1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & -1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 & 0 \\
\end{array}
\right]$
By the energy theorem, the sum over all its matrix entries is the Euler characteristic $\chi(G)=1$. Here is the checkerboard matrix $J$:
$J= \left[\begin{array}{ccccccccc}
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 \\
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 \\
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 \\
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 \\
-1 & -1 & -1 & -1 & 1 & 1 & 1 & 1 & 1 \\
-1 & -1 & -1 & -1 & 1 & 1 & 1 & 1 & 1 \\
-1 & -1 & -1 & -1 & 1 & 1 & 1 & 1 & 1 \\
-1 & -1 & -1 & -1 & 1 & 1 & 1 & 1 & 1 \\
-1 & -1 & -1 & -1 & 1 & 1 & 1 & 1 & 1 \\
\end{array} \right]$
and
$LJ=\left[
\begin{array}{ccccccccc}
2 & 2 & 2 & 2 & -2 & -2 & -2 & -2 & -2 \\
2 & 2 & 2 & 2 & -2 & -2 & -2 & -2 & -2 \\
2 & 2 & 2 & 2 & -2 & -2 & -2 & -2 & -2 \\
2 & 2 & 2 & 2 & -2 & -2 & -2 & -2 & -2 \\
3 & 3 & 3 & 3 & -3 & -3 & -3 & -3 & -3 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}
\right]$
$JL= \left[
\begin{array}{ccccccccc}
2 & 2 & 2 & 2 & 3 & 0 & 0 & 0 & 0 \\
2 & 2 & 2 & 2 & 3 & 0 & 0 & 0 & 0 \\
2 & 2 & 2 & 2 & 3 & 0 & 0 & 0 & 0 \\
2 & 2 & 2 & 2 & 3 & 0 & 0 & 0 & 0 \\
-2 & -2 & -2 & -2 & -3 & 0 & 0 & 0 & 0 \\
-2 & -2 & -2 & -2 & -3 & 0 & 0 & 0 & 0 \\
-2 & -2 & -2 & -2 & -3 & 0 & 0 & 0 & 0 \\
-2 & -2 & -2 & -2 & -3 & 0 & 0 & 0 & 0 \\
-2 & -2 & -2 & -2 & -3 & 0 & 0 & 0 & 0 \\
\end{array} \right]$.
The eigenvalues of $L$ are
$\left\{\frac{1}{2} \left(5+\sqrt{29}\right),\frac{1}{2}
\left(1+\sqrt{5}\right),\frac{1}{2} \left(1+\sqrt{5}\right),\frac{1}{2}
\left(1+\sqrt{5}\right),1,\frac{1}{2} \left(1-\sqrt{5}\right),\frac{1}{2}
\left(1-\sqrt{5}\right),\frac{1}{2} \left(1-\sqrt{5}\right),\frac{1}{2}
\left(5-\sqrt{29}\right)\right\}$
which are numerically given as
$\left\{5.19258, 1.61803, 1.61803, 1.61803, 1., -0.618034, -0.618034, -0.618034, -0.192582 \right\}$
confirming that the number of positive eigenvalues agrees with the number $5$ of even dimensional simplices and the number of negative eigenvalues with the number 4 of odd dimensional simplices. The eigenvalues of $LJ$ and $LJ$ are all 0 except one eigenvalue $\omega(G)=5$. The Perron-Frobenius eigenvector is $\vec{v} = (-2, -2, -2, -2, -3, 0, 0, 0, 0)$ (the sign of course does not matter, we took the sign which matches the explicit formula given for this vector involving Wu intersection numbers.
Here is self-contained Mathematica code explaining things from an other angle. Mathematica is great pseudo code. But of course, you can grab these few lines and try it for other complexes. Take an arbitrary set of sets A and use “Generate” to construct a finite abstract simplicial complex.
Omega[x_]:=-(-1)^Length[x]; DJ[a_,b_]:=DisjointQ[a,b];
EulerChi[G_]:=Total[Map[Omega,G]];
FermiPhi[G_]:=Exp[Total[Log[Map[Omega,G]]]];
Generate[A_]:=Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1]
CL[G_]:=Table[If[DJ[G[[k]],G[[l]]],0,1],{k,Length[G]},{l,Length[G]}];
CB[G_]:=Table[Omega[G[[i]]]*Omega[G[[j]]],{i,Length[G]},{j,Length[G]}];
Energy[G_]:=Total[Flatten[Inverse[CL[G]]]];
G={{1, 2}, {1, 3}, {1, 4}, {1, 5}, {1}, {2}, {3}, {4}, {5}}
L = CL[G]
g=Inverse[G]
J=CB[G]
JL=J.L
LJ=L.J
l=Eigenvalues[L]
v=First[Eigenvectors[LJ]]
wu=First[Eigenvalues[LJ]]
One can reformulate this a bit: given a simplicial complex $G$, denote by ${\rm int}(B(x))$ the vertices of $B(x)$ in the connection graph $G’$. It is the interior of a ball. It is a subset of $G$ but not a simplicial complex. For a star graph G for example and the central node x, we have ${\rm int}(B(x)) = \{ \{x\}, \{ x,y_1 \}, … \{x,y_m\} \}$ which is not a complex as it does not contain the 0-dimensional simplices $\{y_j\}$. The Perron-Frobenius Eigenvector of $L J$ can now be rewritten as $\omega(x) \chi({\rm int}(B(x)))$. It has the eigenvalue the Wu characteristic $\omega(G)=n$.
For geometric graphs the Perron-Frobeinus eigenvector is constant. The reason is that $\chi({\rm int}(B(x))$ is then the $\omega(x)$, the Wu characteristic of $x$. Indeed, for geometric complexes we have $\omega(G) = \chi(G) – \chi(\delta G)$, where $\delta G$ is the boundary of $G$ (the boundary is defined as the set of vertices where the unit ball is contractible, the interior is the set of vertices where the unit ball is a sphere. These definitions make sense for geometric complexes with boundary, which are discrete analogues of manifolds with boundary. Indeed, by definition, the geometric realization of a discrete geometric simplicial complex with boundary is a manifold with boundary. The realization is homeomorphic to a smooth manifold with boundary. As already noted by Whitehead, every compact smooth manifold with smooth boundary can be modeled as such with a finite simplicial complex. For example, for a $k$-dimensional ball, where the boundary is a $(k-1)$-dimensional sphere, we have $\chi(G)=1$ and $\chi(\delta G)= (-1)^{d-1}$ so that $\omega(G) = 1-(1-(-1)^{d})$ which is $1$ for even $d$ and $-1$ for odd $d$. The Wu characteristic of a wheel graph (a 2-dimensional disk) is $1$, while the Wu characteristic of a a cone extension of an octahedron $G$ (a three dimensional ball) is $\omega(G)=-1$.
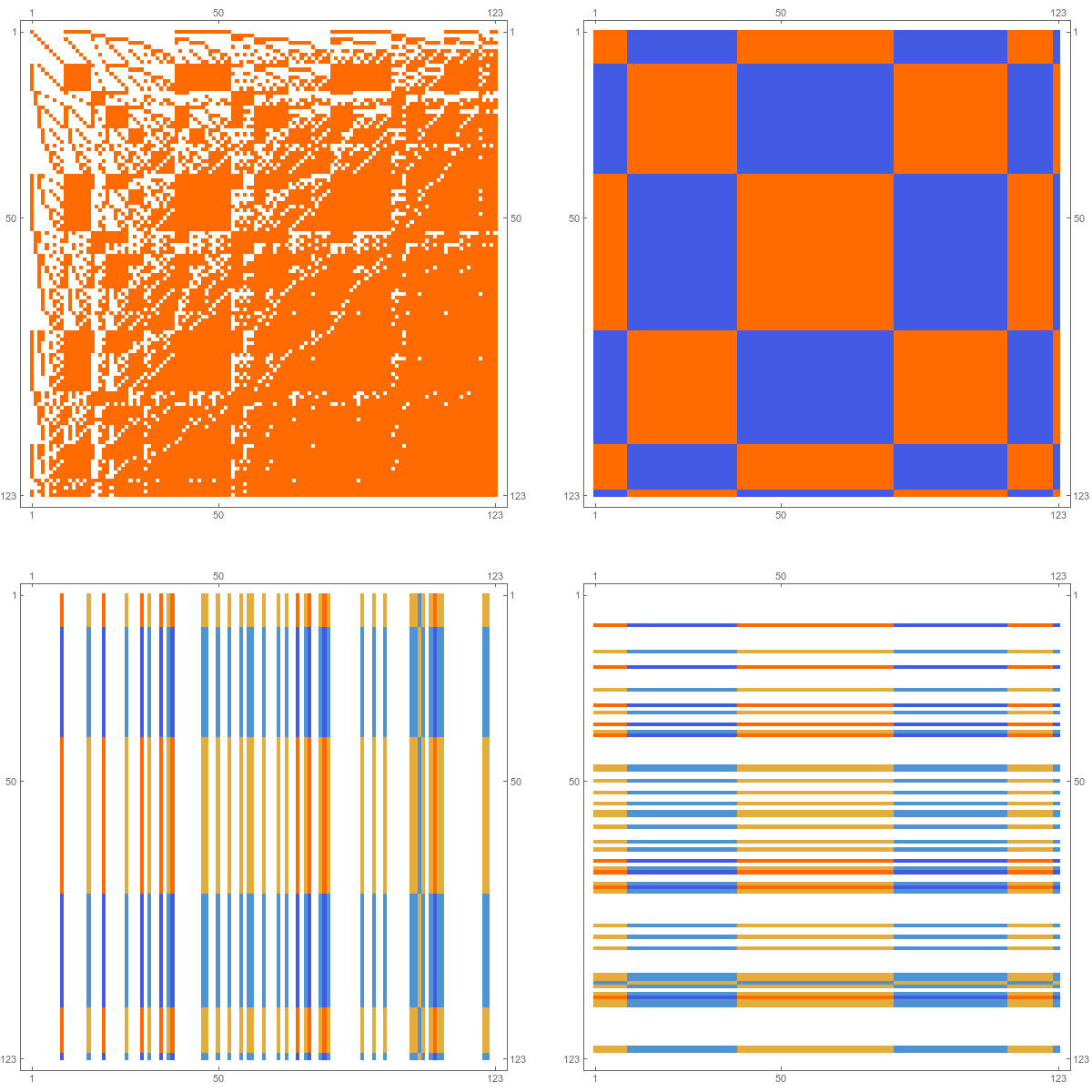
And here is a picture of the matrices $L$, $J$, and then $JL$ and finally $LJ$ for some random complex $G$: