The question
In discrete Poincare-Hopf for graphs the question appeared how to generalize the result from gradient fields to directed graphs. The paper mentions already the problem what to do in the case of the triangle with circular orientation. The triangle has Euler characteristic 1. An integer index on vertices obviously can not exist without breaking symmetry or by doing a random choice which vertex should take the integer value 1.Take the directed triangle with the cyclic ordering 1->2->3->1. Thinking classically, we have to put an equilibrium point in the center of the triangle. It could be a source for the limit cycle on the boundary for example. Cyclic triangles are obviously an obstacle. Can we find a Poincaré-Hopf theorem for a directed graph in which no triangle is cyclic?
Irrotational digraphs
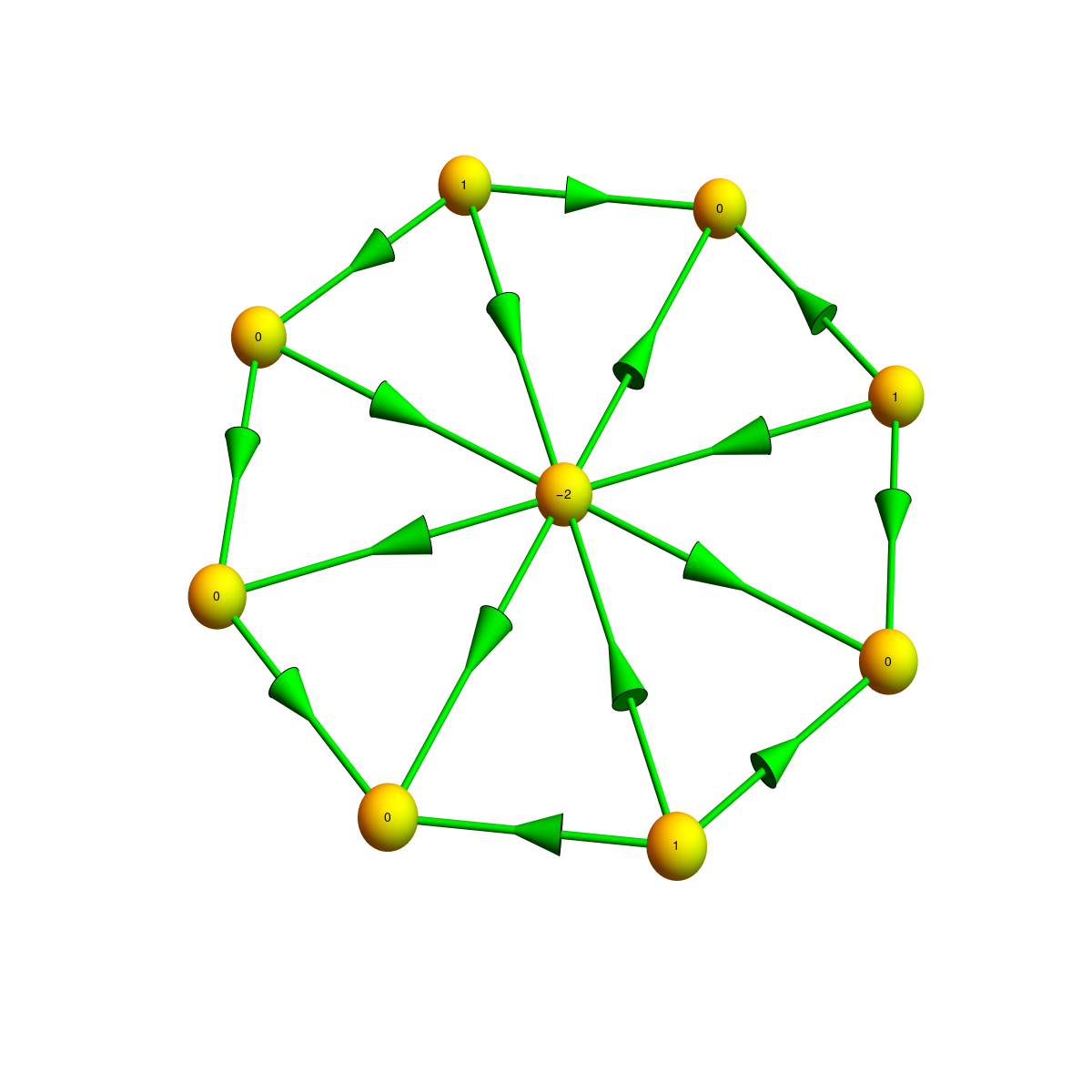
The answer is “yes” and covered in this article. We call a graph without cyclic triangles an irrotational digraph $G$. The Euler characteristic of a digraph is just the Euler characteristic of the finite simple graph in which the direction is discarded. It sums $\sum_x (-1)^{{\rm dim}(x)}$ over all possible complete subgraphs $x$ of $G$. Given an irrotational digraph $G$, define the index
$$ i(v) = 1-\chi(S^-(v)) \; , $$
where $S^-(x)$ is the graph generated by the vertices $w$ with $w \to v$. (The graph generated by a subset $W \subset V$ of vertices is the largest sub-graph of $G$ which contains $W$ as vertex set.)
Theorem: For any irrotational finite simple digraph, $\sum_v i(v) = \chi(G)$.
This theorem implies the theorem for gradient fields proven here: given a locally injective function $g$ (this is also known as a vertex coloring) we have a digraph given by $v \to w$ if $g(v)>g(w)$. Now $S^-(x)$ is the graph generated by the set of vertices with $g(w)<g(v)$. The index $1-\chi(S^-(v))$ is then the index.
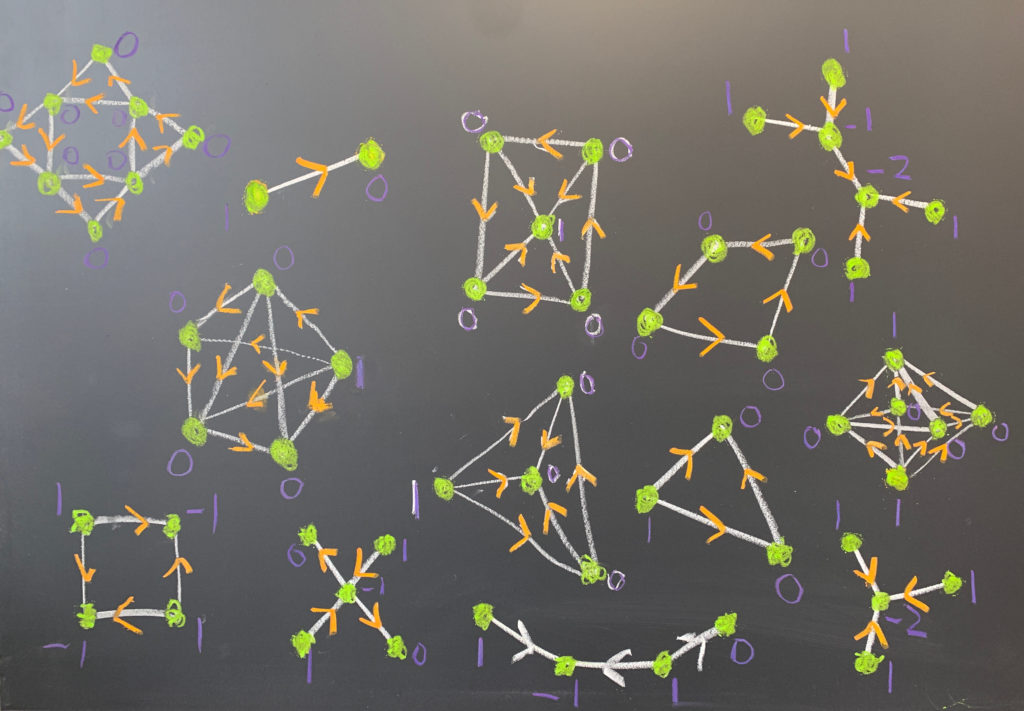
Update Nov 26: here are some familiar situations in 2D. A sink, a source, a saddle with index -1 and a non-Morse situation with index -2. We still have to make sure that there are no cyclic triangles.
 |
 |
 |
 |

[Remark added Nov 20: I had tried in 2012 to submit this to a graph theory journal but it was rejected without a referee report. I don’t need publications, so that I did not bother since, but the theorem is so simple that it hardly needs any peer review. There might have been an other reason for the rejection: for almost the entire later half of the 20th century, graphs were treated as one-dimensional simplicial complexes and this is how many graph theorists still see the subject. Books “belittle” graphs as such. The point of view to see graphs equipped with the Whitney complex (allowing to model much more realistic geometry) came only later. Actually, it had been there since the very beginning (if one looks at Euler and the Koenigsberg bridge problem which models a 2-dimensional situation). It is a bit strange as if one looks at older books in algebraic topology show how the pioneers thought in terms of graphs and hardly in terms of finite sets of sets or higher dimensional realizations (we can not draw in 4D already, but we can draw a complete pentagram, which is a 4 dimensional simplex). As also German mathematicians worked on this, like Hopf (who collaborated in the 30ties with Alexandroff) who would deal with constructs like “Gerüst” which we would today see as the Whitney complex of a graph).
]
Directed simplicial complexes
The theorem is be easier to see if one sees it as a special case of a more general result. One can define more fundamentally what a discrete vector field is on a simplicial complex. Quite a few notions have been introduced for that, for example by discrete Morse theory. I suggested a more quantum mechanical version in the paper about Cartan’s magic formula. That approach has the advantage that the set of vector fields forms a Lie algebra and that it leads to transport flows. This picture sees the wave equation as an average over transports similarly as curvature is an average over indices. Cartan’s magic formula magically goes over to the discrete.
What we did more recently is to explore alternatives and think about more fundamentally what a discrete vector field is. The goal was to find a definition which achieves two things: first of all, it should produce a Poincaré-Hopf formula. Second, it should produce a flow, a map on the vertex set of the graph. The later request is not given when following the arrows of a directed graph as this requires that most nodes are critical points. (If two vectors point away from a vertex, we do not know, where to go. We would have to toss a coin). Fortunately, there are alternatives. Discrete Morse theory leads the way to extend the dynamics from vertices to simplices. However, we chose to use a simpler approach which is partly motivated also by seeing a vector field as a section of a fiber bundle.
The definition is of infantile simplicity (*): if G is the Whitney complex of the graph (V,E), define a map $F: G \to V$ and call the pair $G,F$ a directed simplicial complex. Of course, this is motivated by the case of a directed graph with one dimensional skeleton complex (a case to which of the 20th century graph theory literature has belittled graphs), where G is the union of { { v }, v \in V } and $\{ ( v,w) , (v \to w) \in E \}$. In the later case, one can define $F( {v} ) = v$ and $F( { v,w } ) = v$ if $v \to w$.
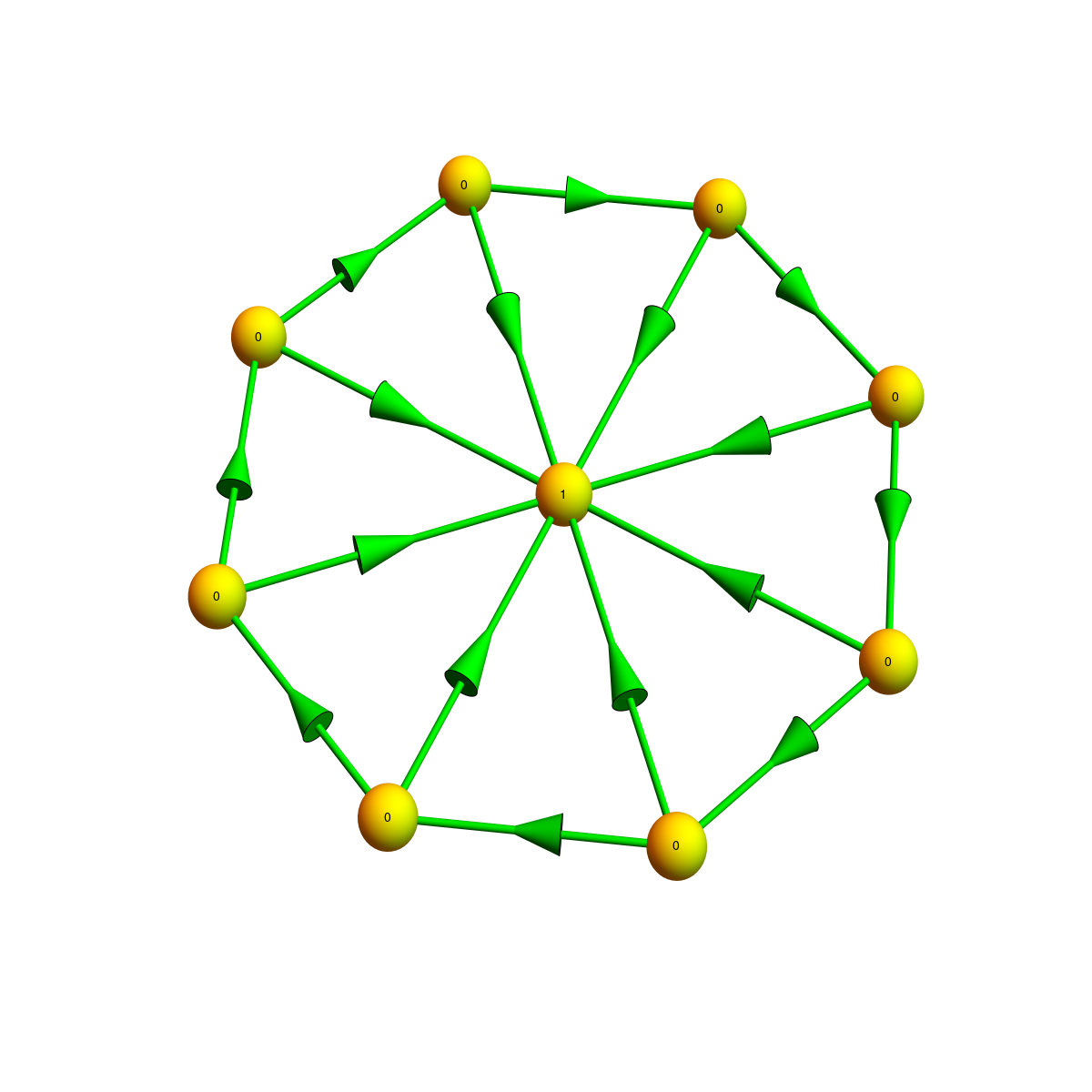
[ (*) this is terminology of Grothendieck who once expressed that the concept of scheme is of infantile simplicity. But to understand the definition of a scheme, one has to know some basic commutative algebra like the concept of spectrum of a ring, the concept of a sheave and the later can only be really appreciated if one knows what a manifold is or differential forms are, the definition of a locally ringed space can only be appreciated when having been exposed to algebraic geometry. I typical third grader has not seen the definition of what an ideal is in a ring. I mean here the term “infantile simplicity” in a literal and not in a metaphorical sense. Indeed, the “new math” wave in the late sixties and seventies, triggered by the Sputnik trauma in the west has led educators to teach set theory in primary school and I myself was exposed to set theory in that age in the form of Venn diagrams which are very accessible to kids. Similarly, also graphs (street maps for example) are accessible to kids (again not metaphorically). If the above definition of a directed simplicial complex is applied to a graph, then indeed, it is infantile as the picture below drawn on a little chalk board shows. It is essentially a directed graph but it also attaches to each triangle a vertex. The Poincaré Hopf theorem assures that the Euler characteristic of the graph which is vertices minus edges plus triangles is equal to the sum of indices which are numbers attached to the vertices.]
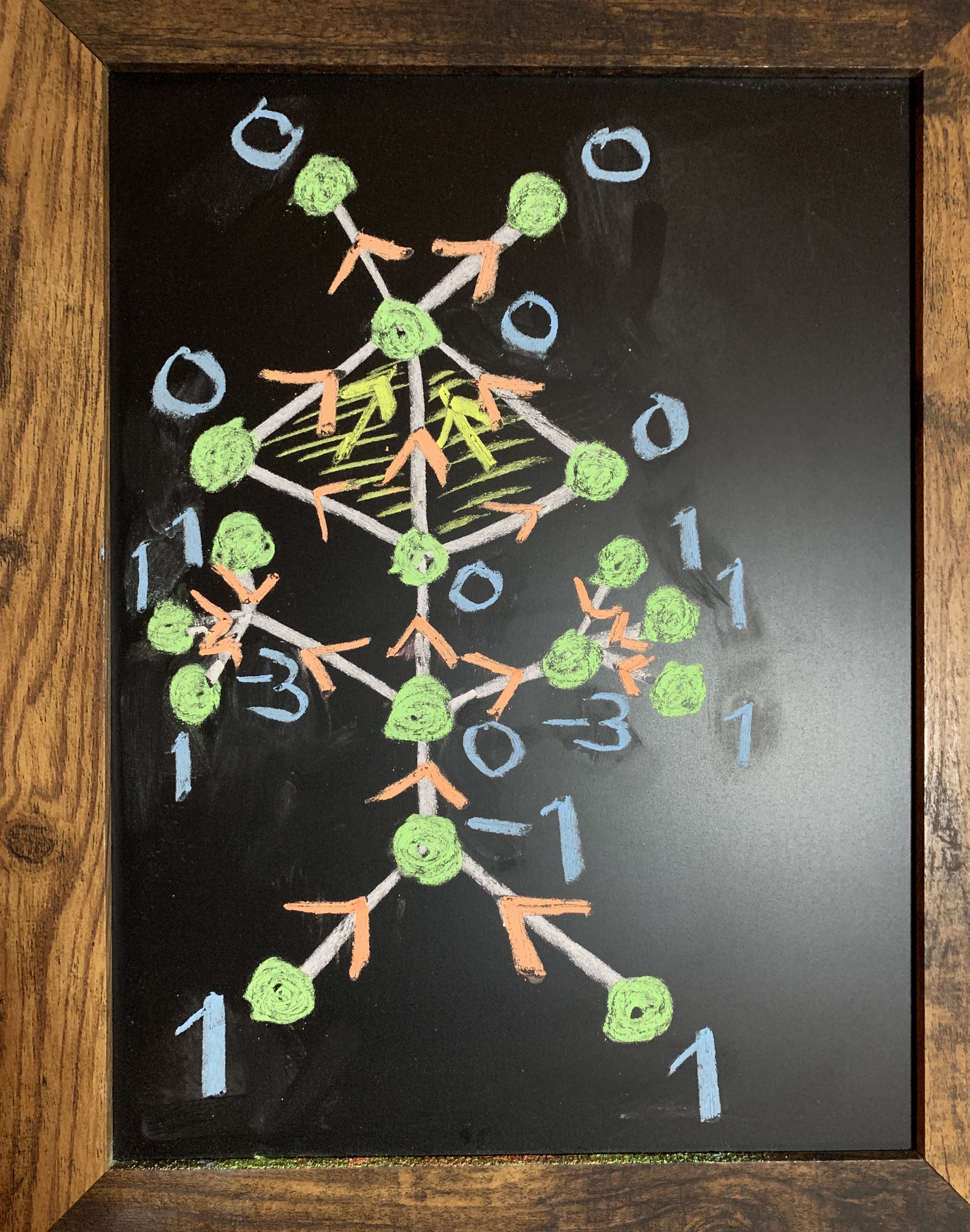
For a directed simplicial complex $G,F$ with vertex set $V = \bigcup_{x \in G} x$, we then define the index function $i(v) = \chi(F^{-1}(v))$. Now,
Theorem: $\sum_v i(v) = \chi(G)$.
To prove as we just shove each energy value $H(x)=(-1)^{{dim}(x)}$ from the simplex $x$ to tje vertex $v = F(x)$. Mathematicians would see the index as the push forward of the measure $\omega$ under the map $F: G \to V$.
Now, if we have a directed graph which is irrotational, then in every simplex x, the directions produce a total order and so a maximal element F(x). Now the index is the index of the map F and the theorem follows from the more general theorem.
Nonstandard analysis

Given a compact Riemannian manifold and a threshold $\delta >0$ and a point $v$, we can look at all non-empty sets which have mutually distance smaller than $\delta$. This is a simplicial complex $H$ with infinitely many sets. The collection $\{ \overline{x} \; | \; x \in H \}$ of compact sets has a compact closure in the Hausdorff metric of all sets in $M$. We can find a finite set $K$ of such sets which contains all standard sets. If $V$ is a finite set which contains all standard elements in $M$, then $G=\{ x \cap V \; | \; x \in K \}$ is a finite abstract simplicial complex. Look now at a differential equation $u’ = f(u)$ and write it as $u(t+dt) = u + dt f(u)$ with infinitesimal $dt$. The picture shows a non-standared circle. Finitely many points are chosen and connected if they are close than a given threshold. This produces a finite abstract complex homotopic to the circle (it is large dimensional in general. Homotopy refers to discrete homotopy.)
Now let $F: G \to V$ be the map which assigns to a set $x$ with accuracy $\delta$ an concrete element $v \in x$. Now let $F(v)$ be a set $y$ closest to $x+ dt f(v)$ representing the points which can be reached when implementing the infinitesimal Euler step. This produces now a sequence $v_k$ of points which represents a numerical computation of the actual orbit $u(t)$ of the differential equation. Actually, the polygon $v_1, \cdots v_n$ follows the orbit $u(t)$. This framework explains why the discrete set-up is natural.

The question is often asked in a physics context: is space a finite set? Can we model physics on a finite set? Is space granular in a very small scale. Very early on like Kustaanheimo, the idea was floated to model mathematics on a finite field (I learned about this from Ernst Specker who also taught us several logic courses. Specker’s student Hans Läuchli taught once an entire calculus course in non-standard analysis (of course it was a follow up logic course and not am actual calculus course, but Läuchli also happened to be my Calc 1 and 2 teacher during my freshmen year, which (of course) was taught in the standard way). In any way, non-standard analysis as constructed by Ed Nelson showed already in 1977 that the answer to the above question is yes, on a very fundamental level. If we model the universe as a compact set (we usually do so or assume manifolds to be compact with a compact boundary), then we can talk about the “standard parts” using finite sets. Functional analysis becomes linear algebra (with some caveats), dynamics becomes maps on finite sets (again with some caveats). Unfortunately, non-standard analysis is peppered with a lot of logical constructs (even by Nelson) which makes it forbidding to teach as a first course in calculus but it is more than that. It is a frame work to think. Just as an exercise, I once presented in a seminar of Specker a proof of the van der Waerden theorem using non-standard analysis by translating the dynamic multi-recurrence proof of Fürstenberg into non-standard analysis. The task is not that difficult because dynamical systems (and especially recurrence questions) are very well suited for non-standard analysis. Nonstandard proofs of the ergodic theorem are the most elegant ones as most theorems in real analysis or in the theory of stochastic processes (actually one of the major fields in which Ed Nelson worked).
[Update November 22, 2019. If found an older write up on this (translated from German notes to English in 1995). It is posted here (careful, it is in a rough state)]
[Update December 21, 2019: In <a href=”https://arxiv.org/abs/1912.00577″>this article</a>, I mentioned the following “simplicial complex”. Given a compact Riemannian manifold M, let V be a finite set containing all standard elements of M. Then form the complex G, containing subsets of M which are infinitesimally close to each other. This is a classical rookie mistake done, when working with IST and I’m glad <a href=”http://u.cs.biu.ac.il/~katzmik/”>Mickhail Katz</a> has pointed that out to me. <a href=”https://arxiv.org/a/katz_m_1.html”>See the articles of MIkhail on the ArXiv</a>. In order to define sets in IST, one has to use internal predicates. One can take a concrete number $\delta>0$ and use this to define a simplicial complex by looking at the Whitney complex of the graph where two elements are connected if their distance is smaller than $\delta$.]
[An other update from December 21, 2019. I just rediscovered the book “infinitesimal calculus” by J. M.. Henle and E.M. Kleinberg in my library (it is not yet scanned in. It is a nice small Dover booklet). It starts with two nice quotes: the classical “God made the integers, all else is the work of men” by Leopold Kronecker is followed by “God created infinity, and man, unable to understand infinity, had to invent finite sets“, which is a statement of Gian-Carlo Rota, who was a torch bearer for finite mathematics. ]


