Having a cohomology for open sets allows to define relative cohomology H(G,K) as H(U). This automatically satisfies excision. It appears that we have a very swift approach to a cohomology satisfying the Eilenberg-Steenrod axioms. There is now a preprint. (now on ArXiv).
Update Mai 25, 2023: while finishing the paper, I could not yet make experiments with knots as the complexes were too big. One strategy was to take a parametrization of a knot K and rewrite this in a product graph where X is is a 1-sphere and K is a 1-sphere. I was interested in the cohomology of the complement
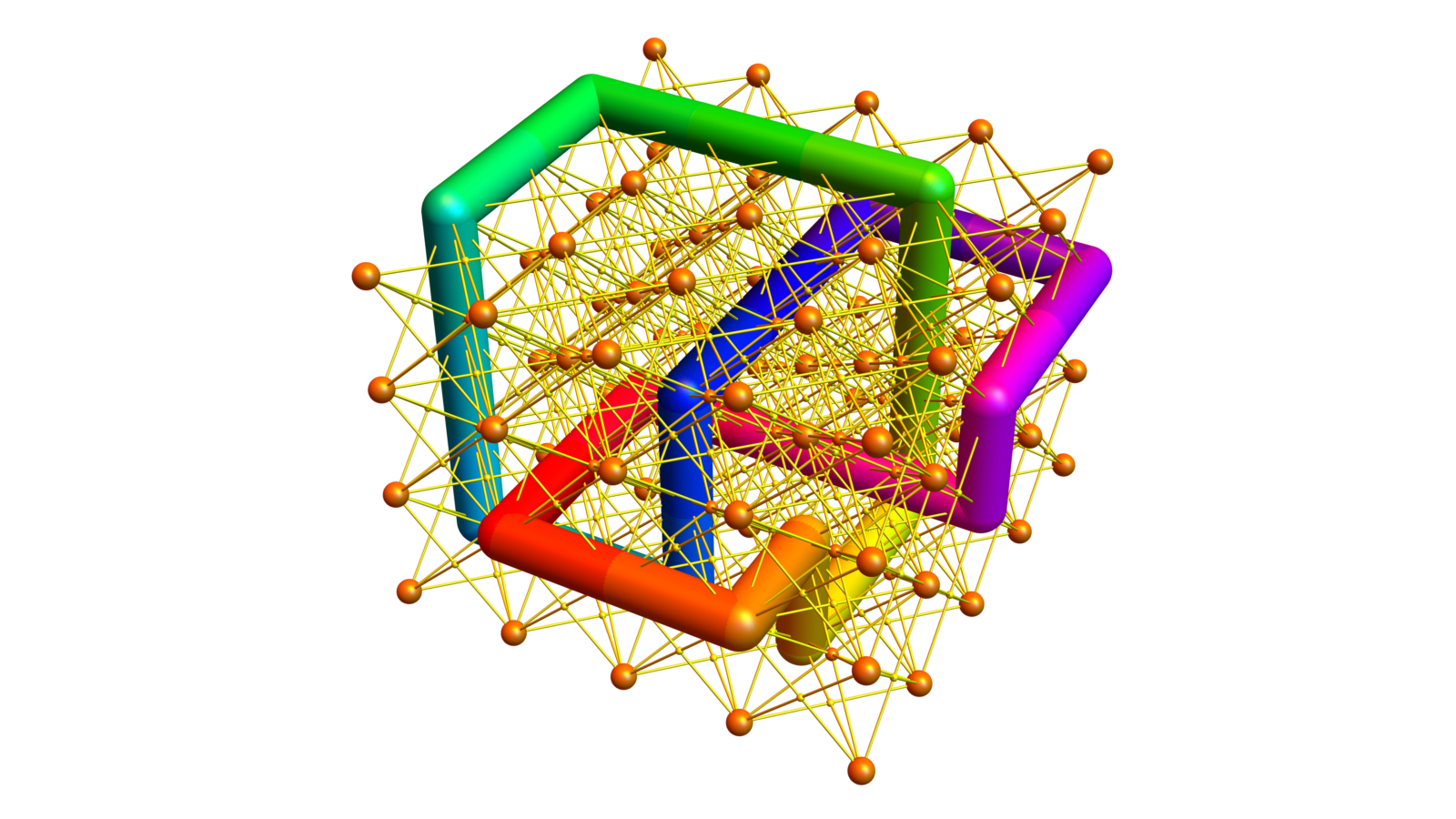
. In the case of an unknot, the matrices are small enough to compute and we see b(U)= (0,0,1,0). Note that b(K)=(1,1,0,0) and b(G) = (1,0,0,0) so that b(I), the interface cohomology is b(I)=(0,1,1,0). I was wondering whether that changes for a knot. It appears not. Here is a situation which I managed to compute. It is implemented in a torus of side lengths 5 meaning that we have 125 vertices. The f-vector is (125, 300,240,64) and Euler characteristic 125-300+240-64=1 (It was easier to not compactify this ball). Then I drew a knot by hand and planted it into G, then computed the cohomology of the complement which has as a 1-point compactification a space of cohomology (1,0,1,0) the cohomology of a sphere.