Shannon Capacity

December 13 update: ArXiv paper.

Claude Shannon was an amazing scientist. He is mostly known for his contributions in information theory, in particular Shannon entropy. Maybe in a time where chess has become popular in particular through the marvelous Queen’s Gambit miniseries, one also should mention that Shannon also wrote one of the first pioneering papers on computer chess. I myself get reminded about Shannon all the time as we live close to his home at the Mystic lakes a place I frequently run around. His estate, the Entropy house of course still stands and was recently renovated (it is a private residence however and is not a museum). A less known quantity introduced by Shannon is the Shannon Capacity. Similarly as Kolmogorov-Sinai entropy measures the exponential growth rate of errors in a dynamical system the Shannon capacity measures the exponential growth of the capacity of a communication channel with prescribed errors if one uses more and more redundant independent channels. One would think that the information capacity of Shannon is multiplicative but already Shannon computed it for an alphabet with 5 letters in which errors can occur cyclically. In that case the one gets not 2 as one would expect but the square root of 5 which is slightly bigger. Shannon himself estimated in that case the value to be between 2 and 2.5. For an alphabet with 7 letters and errors again possible in a cyclic way one does not know the capacity yet! I myself love these type of seemingly simple problems which are unexpectedly damn hard. The entropy problem for dynamical systems on which I worked for a decade with little success is such an example. Number theory problems about primes or factorization are other examples. The Shannon capacity problem is equally beautiful and known to be hard. There are actual mathematical reasons why the general problem must be hard since computing the independence numbers of graphs is a NP hard problem (this is because after dualizing the graph complement, one gets the clique problem which is one of the prototypical NP hard problems). Finding the Shannon capacity is even harder as we need to compute the independence number in a limit of larger and larger networks. So, this not only might be computationally hard but maybe even impossible to determine in general. Difficult problems need not to be difficult for subclasses however The entropy problem for dynamical systems is easy for example for group translations or some subshifts of finite type. The Hamilton path problem for graphs is difficult in general but easy for combinatorial manifolds which are all Hamiltonian, independent how large they are, the reason being that we can explicitly construct Hamiltonian paths for such manifolds. We will just see that one can compute the Shannon capacity of a class of networks quite easily.

Finite simple graphs can be multiplied by taking the Cartesian product of the vertex set and connect to points if the projection to both graphs is either a vertex or edge. We can therefore form the n’th power of a graph. The independence number of a graph is the size of a maximal set of independent vertices. A set is independent in a graph if they are all pairwise not connected. When looking tat the graph complement , the independence number of is equal to the clique number of . The Shannon entropy therefore measures the exponential growth rate of the maximal clique size in the large product of powers of a graph. It is a very natural notion. As usual, once you have seen why it is important it is obvious why it is important but it was the genius of Shannon to actually see it the first time. The reason why this information capacity is important is because if one can look at a graph as an alphabet with error relations. This tells which letters can be confused. For example, in our usual ASCII alphabet, the letter O and the letter 0 can easily be confused as does 1 and l (the lower case L letter) or I, the capital I letter. Usually, such errors can be corrected by context. We see frequently that after applying OCR programs to pictures that certain letters are mistranslated but because of the context, we often can recover the text. If we transmit not one encoding of the text but 2 encodings, then we need twice as much information but also allow for more recovery. One would think that the errors also multiply but this is not the case. From a practical point of view one wants to optimize the code and taking multiple copies is a possibility to improve the band with of the code. In some sense, the Shannon capacity measures the ultimate best way we can do with taking multiple copies of the code. Here is my own contribution to this topic. Its very small but a bit surprising at first: there is a large class of networks A for which we can compute the Shannon capacity explicitly: these are connection graphs A of finite abstract simplicial complexes. Remember that a simplicial complex is a finite set of non-empty set closed under the operation of taking finite non-empty subsets. They define the connection graph in which the sets are the nodes and two different sets are connected if they intersect. Here is the theorem:

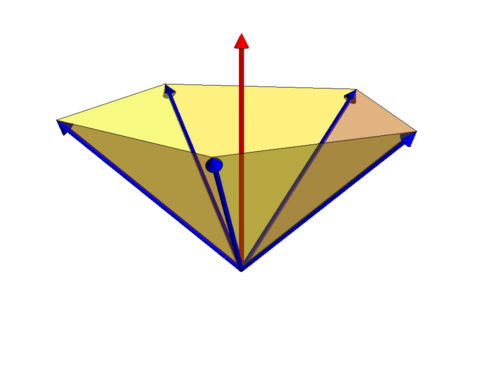For a sketch of the proof and a bit more other things, see this youtube presentation. The lower bound on the Shannon capacity is the independence set, which is m. To get the upper bound we construct a “Lovasz umbrella” in which is given by n unit vectors in this space such that two pairs u(x),u(y) are perpendicular if the sets do not intersect. Then take the umbrella stick . The secant square of the largest angle between the vectors an the stick is the Lowasz number which is an upper bound for the Shannon capacity. The independence number is not multiplicative with respect to the graph product but the Lowasz number is, which is a reason that it is an upper bound. In our case, the orthogonal Lowasz representation is easy to compute. Just take if j is in x and else and then normalize. The secant squared of the largest angle is then m forcing the Shannon capacity to be m. Pretty amazing that one can compute the Shannon capacity for these type of graphs.

[Update December 11: a bit more about the math: ]