The quantum plane - Quantum Calculus

Update of May 27, 2017: I dug out some older unpublished slides authored in 2015 and early 2016. I added something about the quantum gap and something on the quantum plane at the very end. Here is the presentation, just spoken now.

The quantum line

In one dimension, there is a natural compact metric space D on which one has a translation group which features a smallest unit. The group D of dyadic integers is the Pontyagin dual of the Pruefer group and is a natural “one-dimensional quantum space”. The real analogue is the circle, a compact topological group which is the dual of the integers and a quotient of the real numbers. The translation on D is called the adding machine. It is known in ergodic theory as the von Neumann-Kakutani system. Part of my thesis dealt with this system as it appears naturally in the context of renormalization of Jacobi matrices $L \mapsto L^2 + c$ , a complex dynamical system in a non-commutative space. The non-commutative Julia sets constructed there produced interesting examples of almost periodic operators. What I did in my thesis is to get from any random Jacobi operator L on (X,T) a new Jacobi operator D on (X1,T1) such that D^2+c = L holds. The matrices one gets in the limit have the spectrum of the Julia set of the map $z -> z^2+c$ . The matrices had already been introduced by G.A.Baker, M.L. Mehta, D.Bessis, P.Moussa in the 80ies. A new point in the thesis was to see the renormalisation on a non-commutative Banach algebra of operators, crossed products of a commutative Banach algebra defined by an automorphism. Ergodic theory so naturally introduces the group of dyadic integers just by renormalization: the renormalization map is the 2:1 integral extension. Take two copies X1,X2 of the probability space, then map using T from X1 to X2, and then use the identity to get back from X2 to X1. What happens is that the renormalization picture directly gives the nature of the self-similar operators. They are almost periodic matrices. After having worked on Barycentric refinements of complexes, a new point of view appeared: the dyadic group of integers is the Barycentric limit of a one dimensional complex. It is the unique attractor of the Barycentric refinement operation. Here is a simple illustration of the non-commutative Julia renormalization: we see the Kirchhoff matrix of a circular graph $C_8$ :

$\left[ \begin{array}{cccccccc}2&-1&0&0&0&0&0&-1\\-1&2&-1&0&0&0&0&0\\ 0&-1&2&-1&0&0&0&0\\ 0&0&-1&2&-1&0&0&0\\0&0&0&-1&2&-1&0&0\\0&0&0&0&-1&2&-1&0\\0&0&0&0&0&-1&2&-1\\-1&0&0&0&0&0&-1&2\\ \end{array} \right]$

The matrix 4 B – B.B decomposes into two copies of the Kirchhoff matrix of C₄:

$\left[\begin{array}{cccccccc} 2&0&-1&0&0&0&-1&0\\0&2&0&-1&0&0&0&-1\\-1&0&2&0&-1&0&0&0\\0&-1&0&2&0&-1&0&0\\0&0&-1&0&2&0&-1&0\\ 0&0&0&-1&0&2&0&-1\\-1&0&0&0&-1&0&2&0\\0&-1&0&0&0&-1&0&2\\\end{array}\right]$

Indeed, the Julia set of the quadratic map $T(z) = z(4-z)$ is the interval [0,4]. This picture gives the density of states in the Barycentric limit of a one dimensional simplicial complex. Apropos: here are two unusual photos of Julia and Fatou. They are from the book of Michele Audin “Fatou, Julia, Montel”, Springer Lecture Notes in Mathematics 2014. Click on the picture to see it large:

Two dimensional quantum space

We tried to get a grip on higher dimensional versions here [PDF]. The following construction was done in thesis (page 250) We proved that the renormalization map for Z^d systems has a unique fixed point. Lets look at the construction in two dimensions:

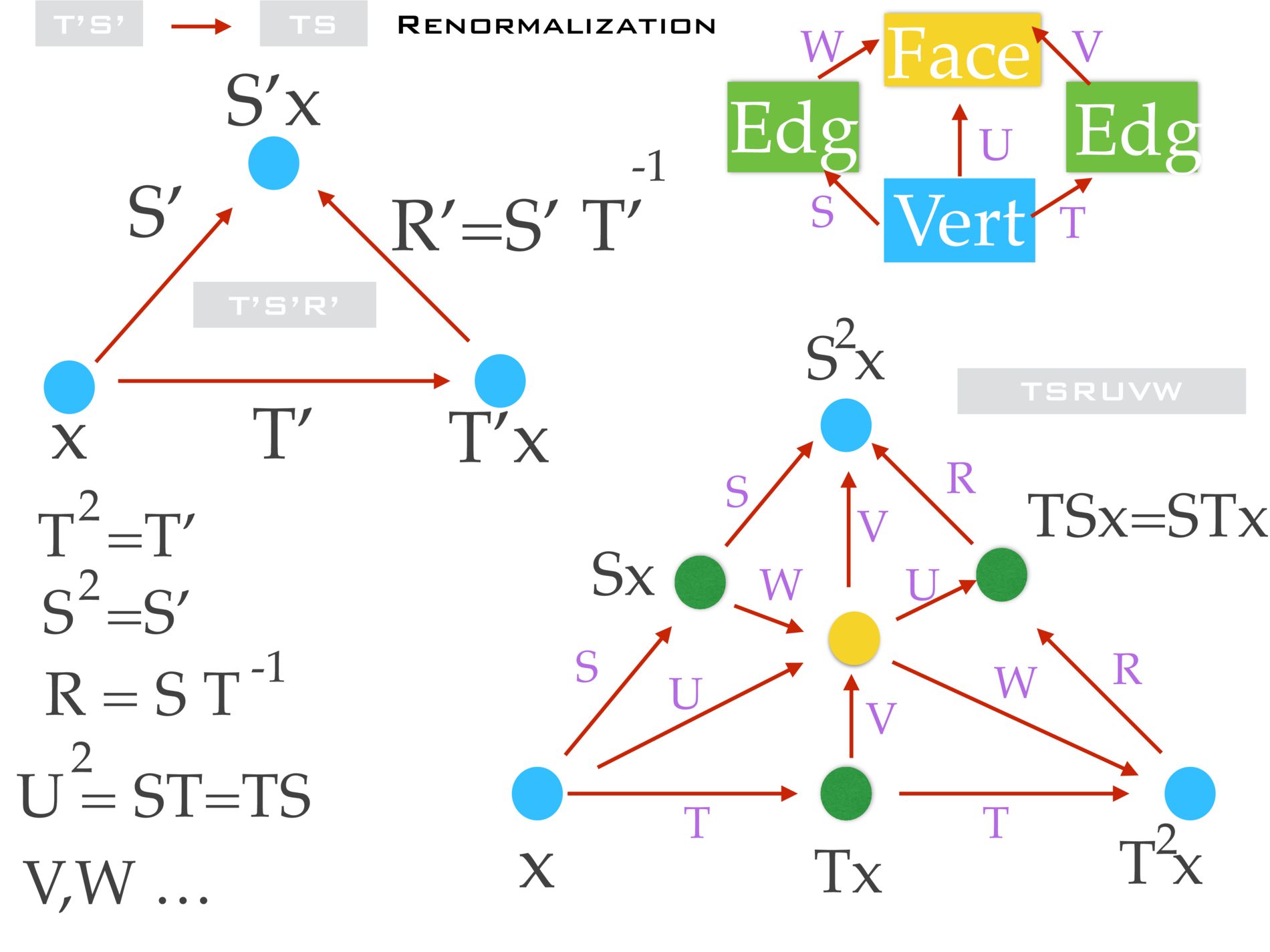
In October 2015, we started to investigate the Barycentric limit in the 2 dimensional case. It is a renormalizaation story on pairs (T,S) of commuting measure preserving transformations. This generalizes the von Neumann-Kakutani case. First make integral extensions T_1^2=T, S_1^2=S, U^2 = ST = TS.

Definition. Let T,S be a pair of commuting automorphisms (measure preserving invertible maps) of a Lebesgue space, (a standard probability space) X. Define a new system by taking a union of 4 copies of X₁,X₂,X₃,X₄.

On X1, define T1: X1 -> X2     x -> Tx
On X1, define S1: X1 -> X3     x -> Sx
On X2, define T1: X2 -> X1     x -> x
On X2, define S1: X2 -> X4     x -> Sx
On X3, define T1: X3 -> X1     x -> x
On X3, define S1: X3 -> X4     x -> Tx
On X4, define T1: X4 -> X3     x -> Sx
On X4, define T2: X4 -> X2     x -> Tx

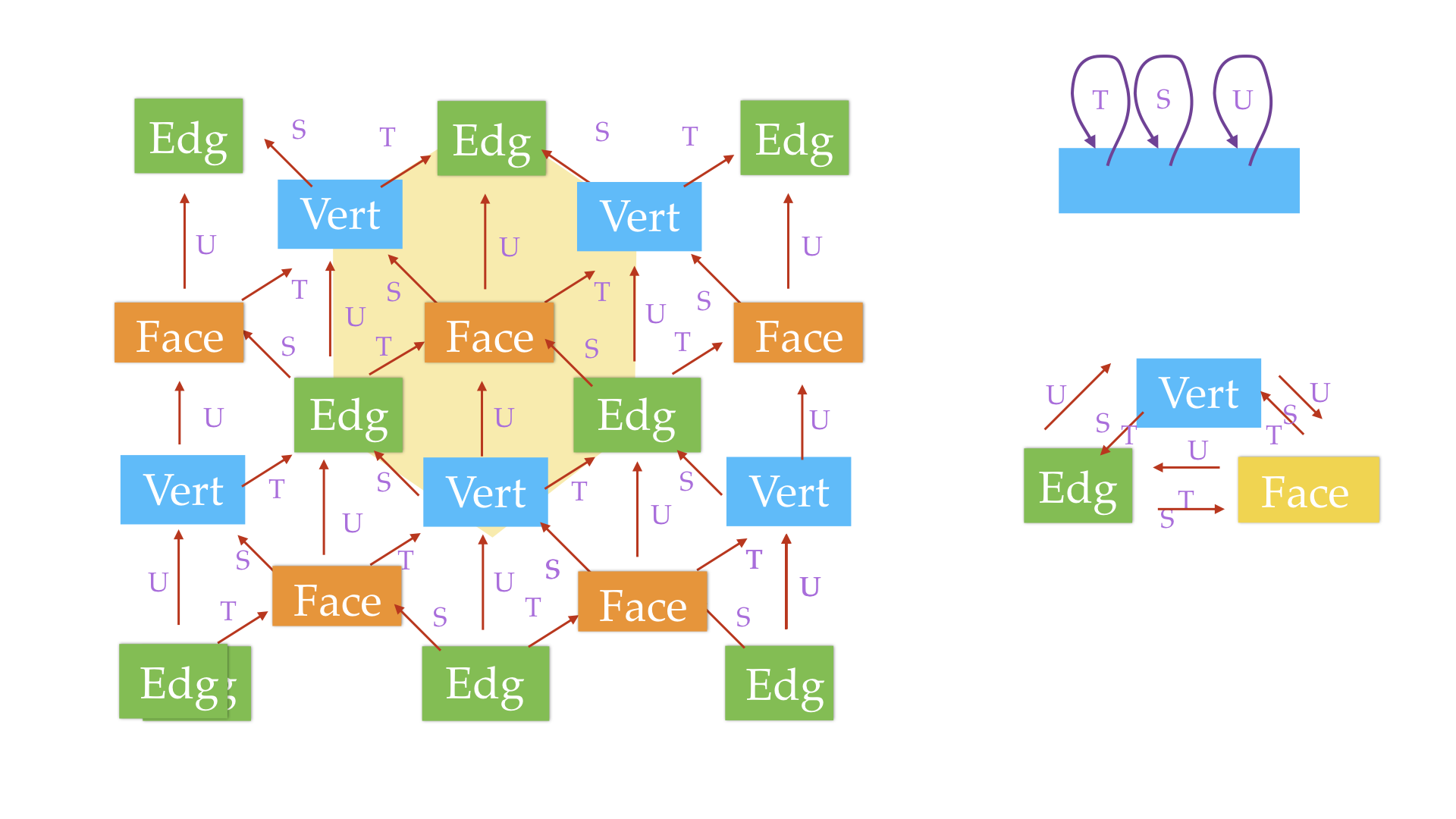
Now, $T1^2=T1$ , $S1^2=S1$ and $T1 S1 = T2 S1$ . We have a renormalization map $(X,T,S) \to (X1,T1,S1)$ of commuting maps. It is a contraction on Z² actions if we take the metric $d( (T,S),(U,V)) = m( \{ x \; |\; T(x) \neq U(x) or S(x) \neq V(x) \}$ . The limiting system is a compact topological group with a $Z^2$ action having a unique invariant measure. There is an additional symmetry B, the Barycentric refinement. Still we struggle to get from that space pictures of Barycentrically refined geometric spaces. It seems that we have to introduce on each level more and more transformations (defined by the two basic transformations T,S). Here is one attempt to get a grip on the refinement step:

A martingale idea

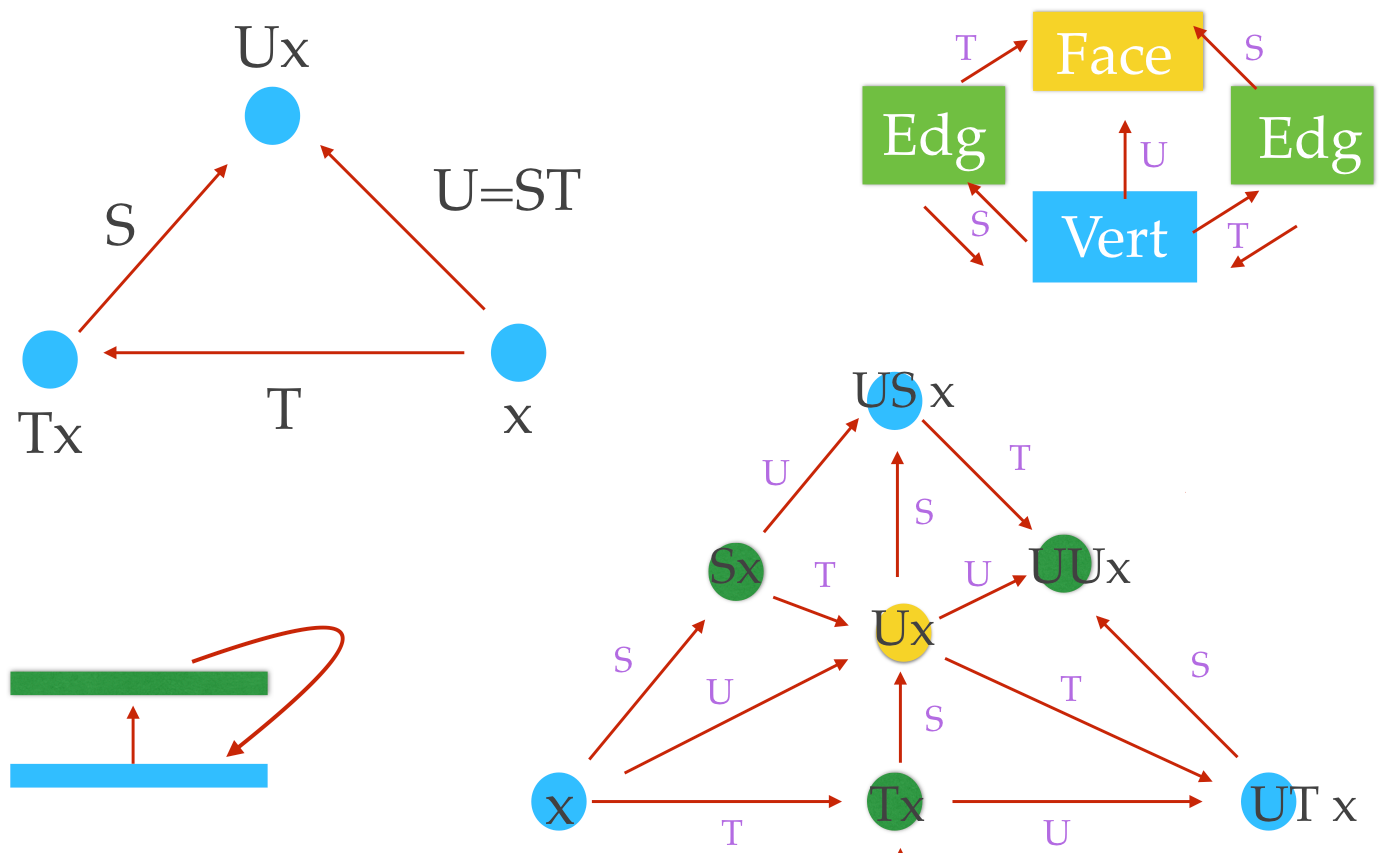
But that produces a mess of transformations. It would be nicer to have only two transformations and look at their orbits. Depending on the sigma-alrebra used, we would get the individual Barycentric refinements. This is kind of a Martingale idea: play with the $\sigma$ – algebras rather than with the transformations. Here is the picture: we always work only with two transformations S,T and a helper transformation U=ST=TS. What happens after the first step is that we have now 6 triangles. The central face has degree 6. On the edge, say Tx, the outgoing transformation T gets us back to x because the sigma-algebra tells us so. On the next level each of the triangles will again be refined:

Here is an other doodle. It might be better to renormalize the Z² action with tripling the probability space each time:

The quantum line

Two dimensional quantum space

A martingale idea

Author: oliverknill