A mass gap in the Barycentric limit

The Barycentric mass gap

In physics, a mass gap is the difference , where is the energy of the vacuum state and is the next larger energy state of the Hamiltonian. This is a bit vague as stated because one has to give first the Hamiltonian. Constructive quantum field theory makes the definition and the problem precise. We look here at a purely geometric and much more elementary problem: given a type of Laplacian for a finite abstract simplicial complex G, we say that the complex G has a mass gap at 0 for the Laplacian, if the Barycentric limiting density of states dk(G) has an open interval containing 0 which has zero measure. We know already that for one-dimensional complexes, the Kirchhoff Laplacian or the Dirac Laplacian have both no mass gap (the reason being that in that case we know everything explicitely, similarly as in probability theory, we know everything in the Gaussian case). We prove here that for the connection Laplacian (the symmetric matrix which has L(x,y)=1 if x and y intersect and L(x,y)=0 else), there is a mass gap containing the interval (-1/5,1/5).

Review of the Barycentric limit theorem

The density of states of the Laplacian L of a finite simplicial complex G can be seen as a “law” of the complex G. It is a discrete point measure on the real line, where the individual atoms represent the eigenvalues. We have shown in 2015 that if G is iteratively Barycentric refined, then the law converges universally to a limit which only depends on the dimension of the complex. For the proof in the case of the Kirchhoff matrix, see here on the ArXiv or on this blog. As mentioned in that paper, the result is quite flexible. One can replace the Kirchhoff Laplacian with any type of Laplacian which is local or decays fast enough. An other example is the Dirac operator D=d+d^*. The proof (which is maybe of the same overall low complexity than the proof of the central limit theorem in a parallel probabilistic situation) certainly also works for the connection Laplacian L, which lives on the same Hilbert space than the Dirac matrix D. We have seen that in the one-dimensional case, everything is completely understood, if L is the Kirchhoff Laplacian. The limiting measure in the Kirchhoff is absolutely continuous with explicitly known density of states which is an arcsin distribution. In dimensions d>1, the support of the density of states appears fractal. What happens in the connection case?

P.S. a bit of the history: the limiting spectra for Barycentric refinements of the triangle (the Stricharz carpet) have first been studied experimentally in the “BeKeNePaPeTe” paper of M. Begue, D.J. Kelleher, A. Nelson, H. Panzo, R. Pellico, A. Teplyaev in 2012. We realized and proved in the summer of 2015 that the density of states for any simplicial complex converges universally depending only on the dimension of the complex. August 2015 and September 2015. (The first paper was too drafty for submission to a journal, the second still contained too many remark. I might try to publish it at some point, but there is no rush.)

A mass gap for connection Laplacians

The concept of a mass gap sounds fancy since it is one of the Millenium problems. It is the problem to prove a spectral gap in a constructive quantum field theory. We do not deal with that. The Millenium problem dealing with the mass gap in Yang-Mills theories defined in an axiomatic quantum field theory is much too difficult for us. It is probably the least well clear-cut problem of all the Millenia problems as in mathematical physics, there are various levels of rigor and frame works and opinions. Our case is much easier. It is just linear algebra. For simplicial complexes, the Barycentric mass gap problem asks whether in the Barycentric limit, there is an interval (-a,a) outside the support of the universal limiting density of states. We know in the Kirchhoff or Hodge case that the answer is “no” in dimension d=1 and “maybe yes” for dimensions d>1. After having worked quite a bit with connection Laplacians lately, we looked now also at the mass gap problem for connection Laplacians. Here, the answer is very simple and can be given in dimension 1:

The limiting density of states of the connection Laplacian of simplicial complexes has a mass gap for d=1. The interval (-1/5,1/5) has measure zero in the Barycentric limit.

Proof. By the unimodularity theorem, the Green function g=L^-1 is also a Laplacian type operator. If x and y are two faces which do not intersect, then both L(x,y) =0 and g(x,y)=0. In the one dimensional case, the number of connections is bounded above by 5 (at least for almost all connections in the limit). This implies that the spectra of L and g are both contained in [-5,-1/5] union [1/5,5]. Since L has both positive and negative eigenvalues, there is a spectral gap.

Here is a picture of the gap in one dimensions for the connection Laplacian and to the right, the old picture of the limiting spectral function for the Kirchhoff Laplacian

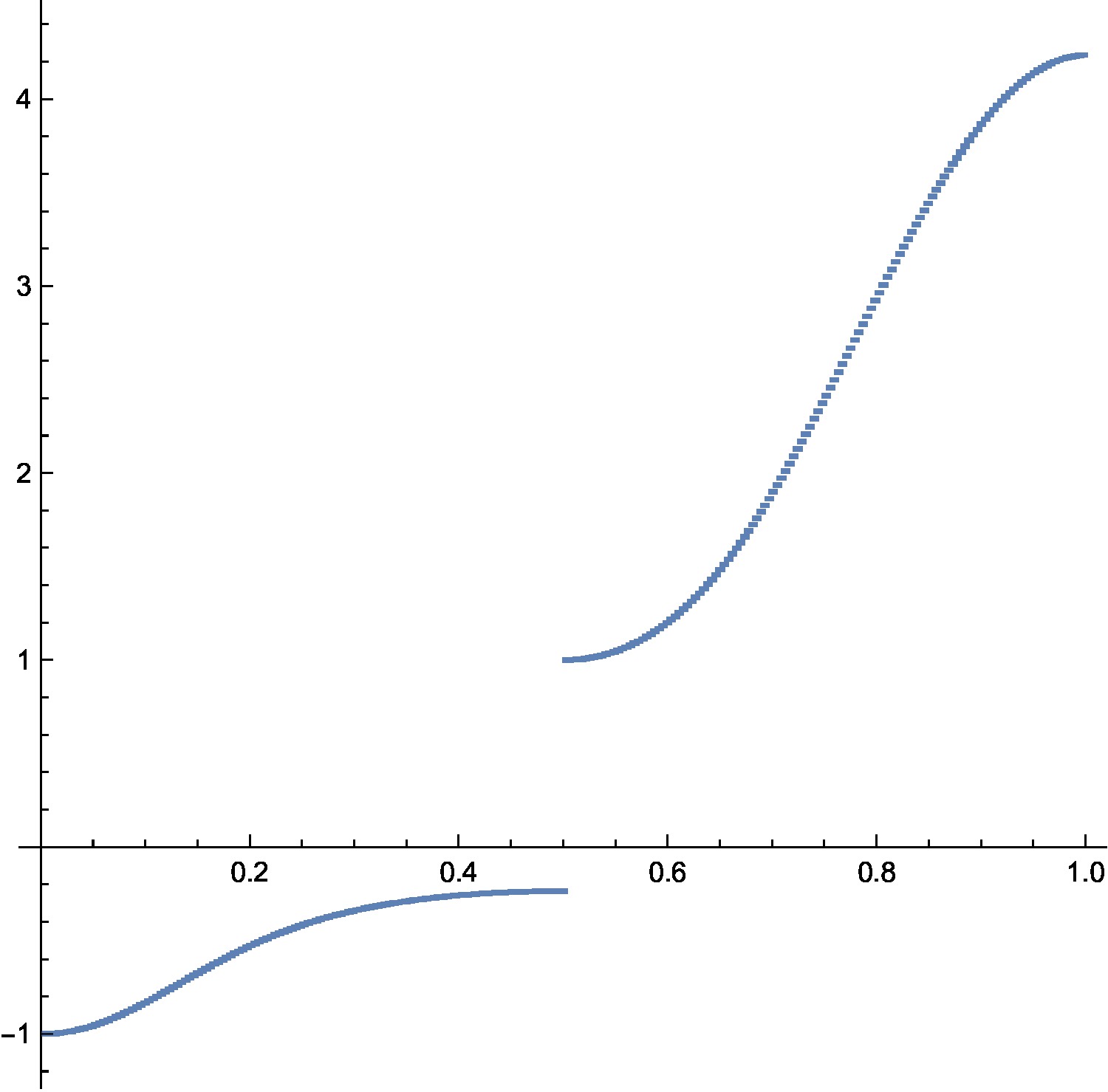
In higher dimensions, the norm of and both converge to infinity as the vertex degrees of the graphs G_n explode. Because for symmetric matrices, the spectral radius is the norm, the spectrum of the Laplacian gets closer and closer to 0. It is still possible that a gap develops.

As for the connection graph, we are in a non-commutative set-up, we can not just diagonalize the situation as in the Kirchhoff case. There is no doubt however that there is like in the Kirchhoff case an explicit formula for the eigenvalues and so for the density of states.

In the Kirchhoff one-dimensional case, the spectral function, the inverse of the integrated density of states was . We see in the connection graph two functions of this type. Here was the picture of the spectral function , the case we understand.

At the moment, we still don’t have an explicit formula for F in the connection case. But we see that the gap ends at 1.

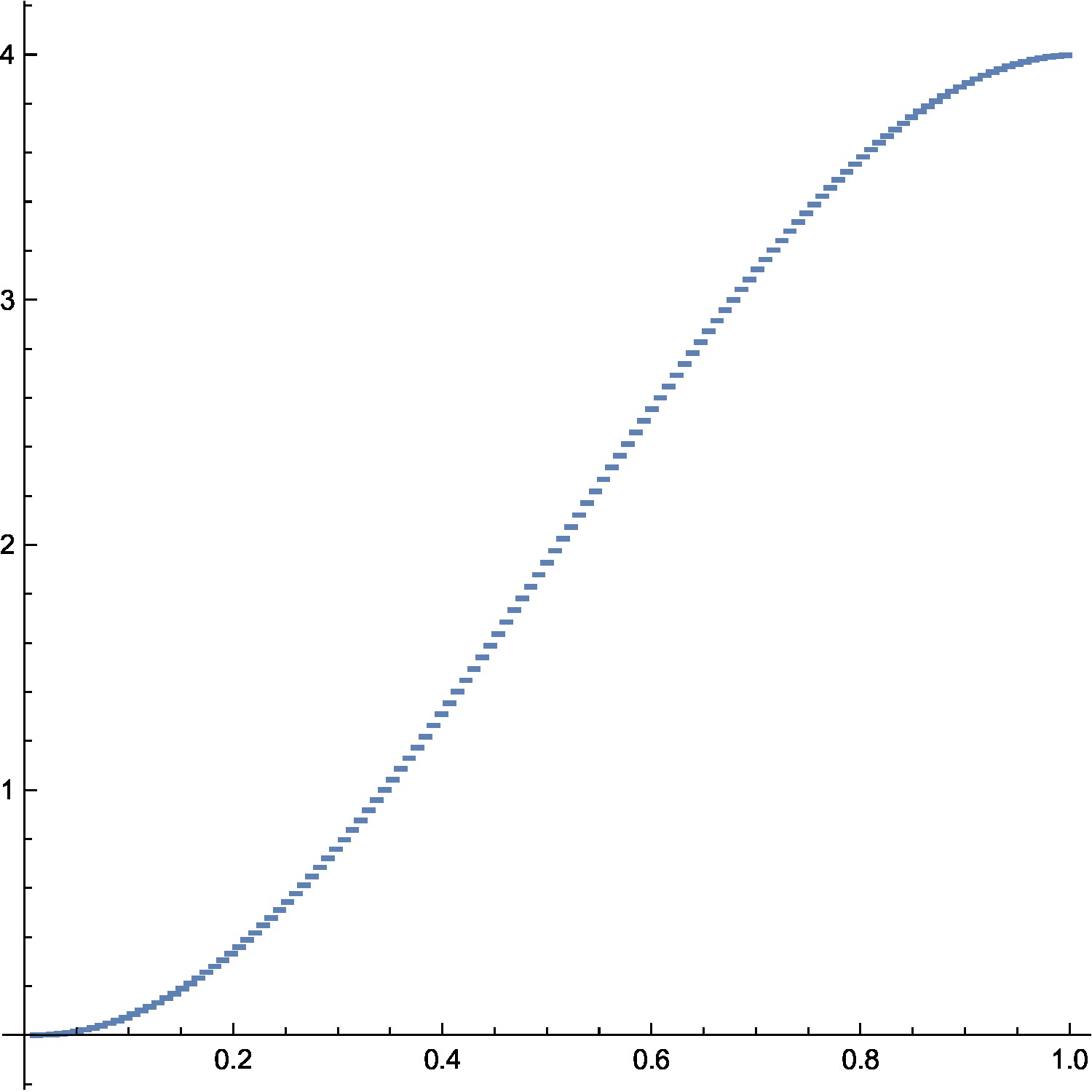
The higher dimensional case is completely open. Lets just show two pictures. To the left the spectral function in the Dirac case D (where also, unlike in the Hodge D² or Kirchhoff L₀=d d^* case, the eigenvalues can become negative), to the right we see the spectral function in the connection Laplacian case:

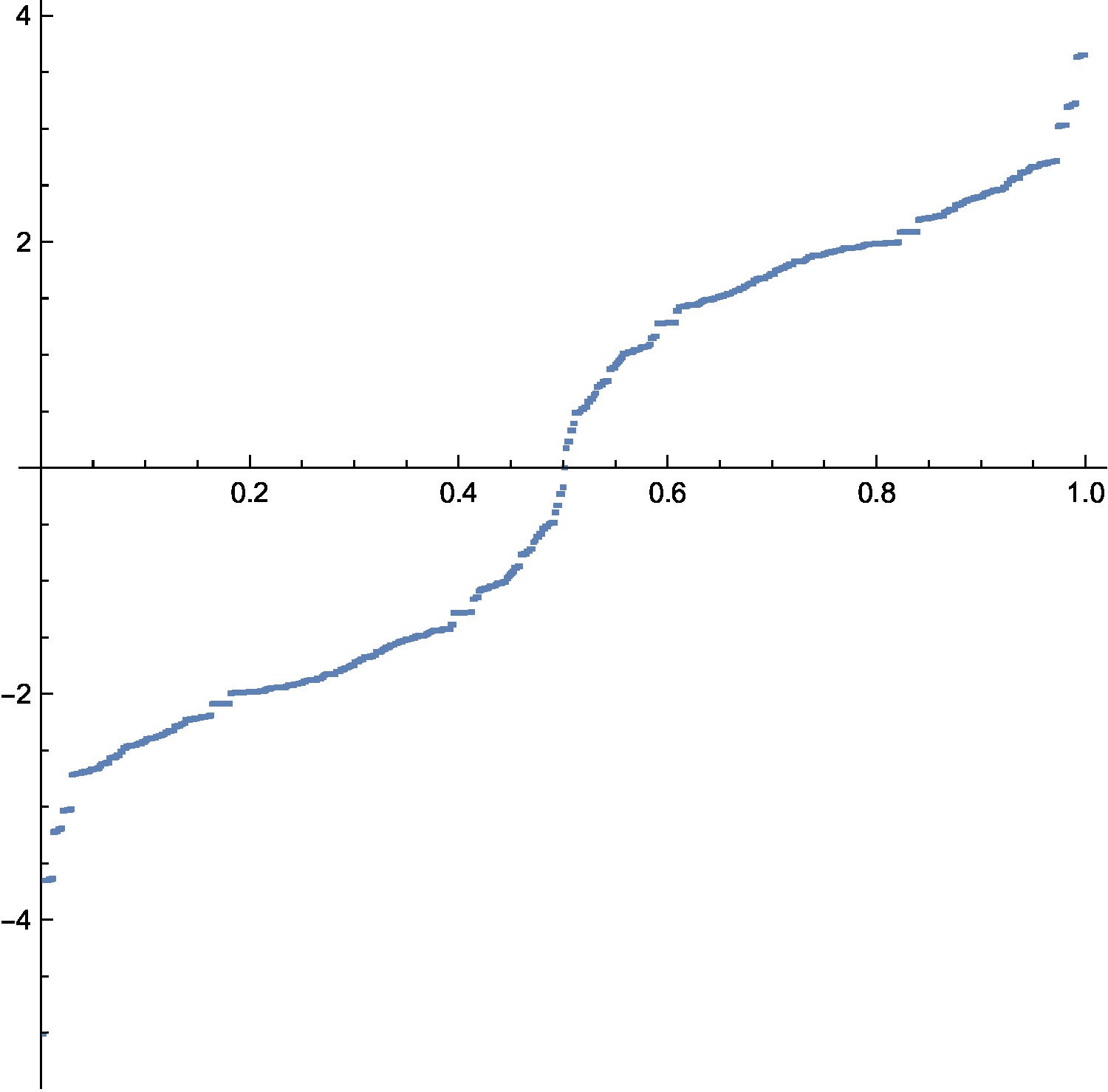
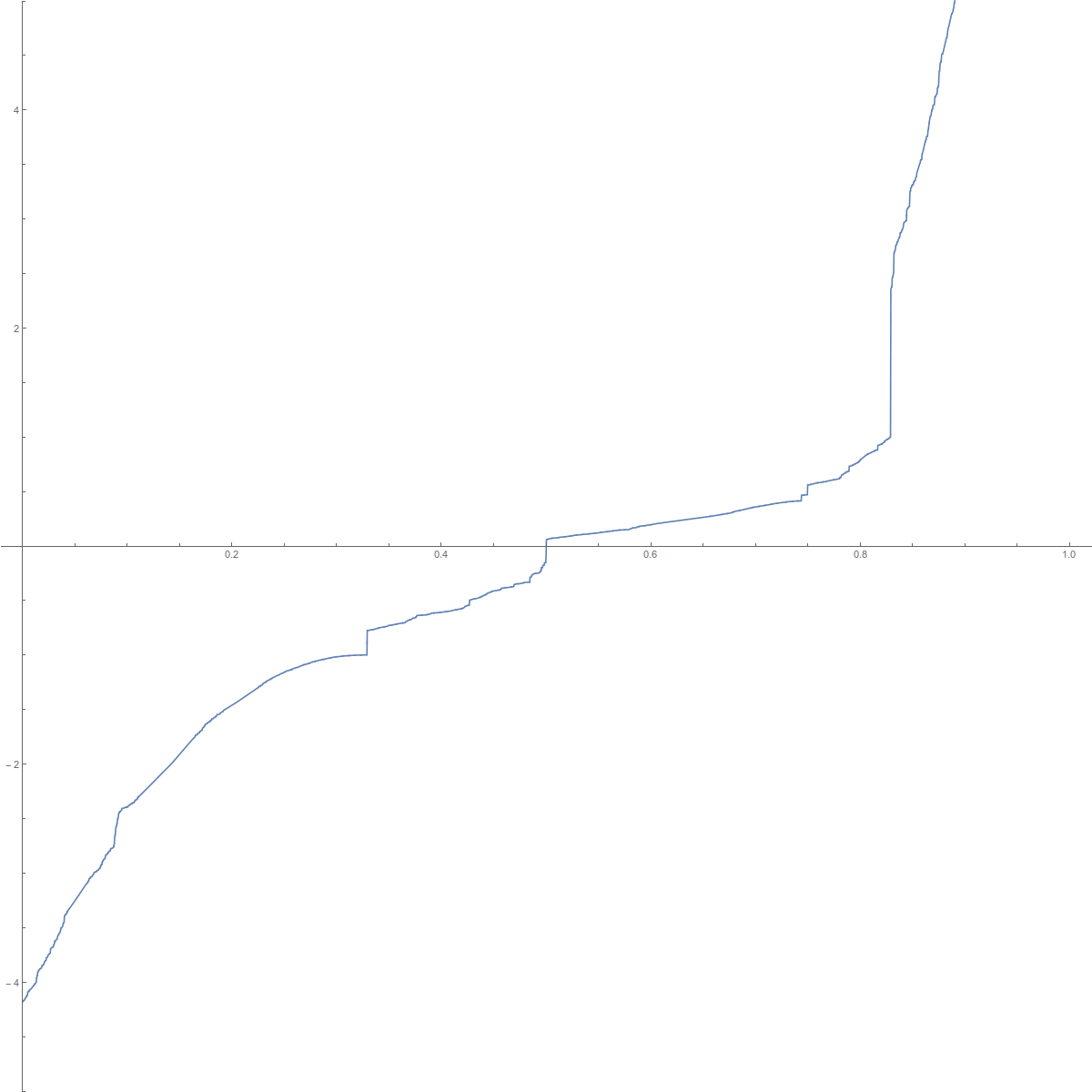
We know that in every step, in the connection graph case, 0 is not an eigenvalue due to the unimodularity theorem. We also know, as the inverse g (the Green function) has larger and larger norm, that in every step, the mass gap around 0 becomes smaller. This does not mean however that there is no mass gap in the Barycentric limit. What is perfectly possible is that the limiting density of states has support away from an open interval at 0 but we don’t know that. The experiments show gaps appear at various places so that it is not clear what happens in the limit.

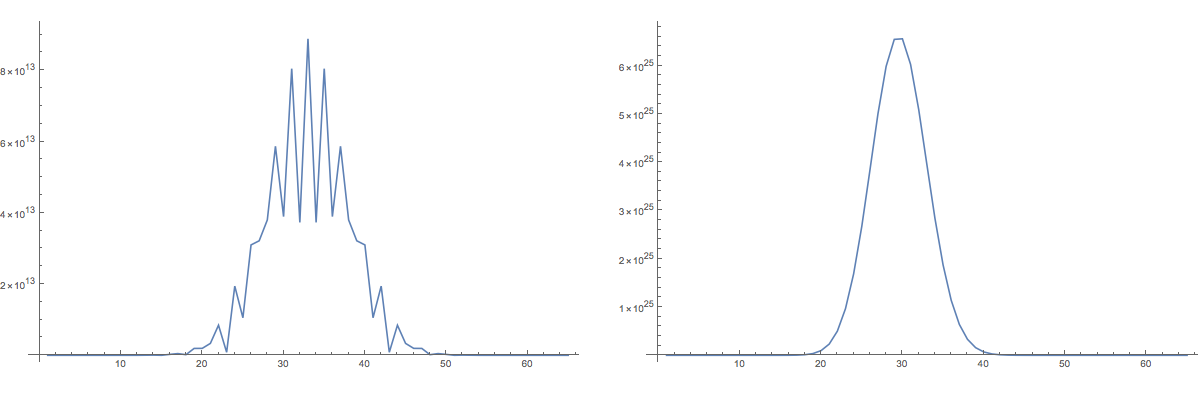
Here is an experiment comparing the coefficients of the characteristic polynomial of the connection Laplacian and then the Kirchhoff matrix. In both cases, after a Barycentric refinement, there is a symmetry.

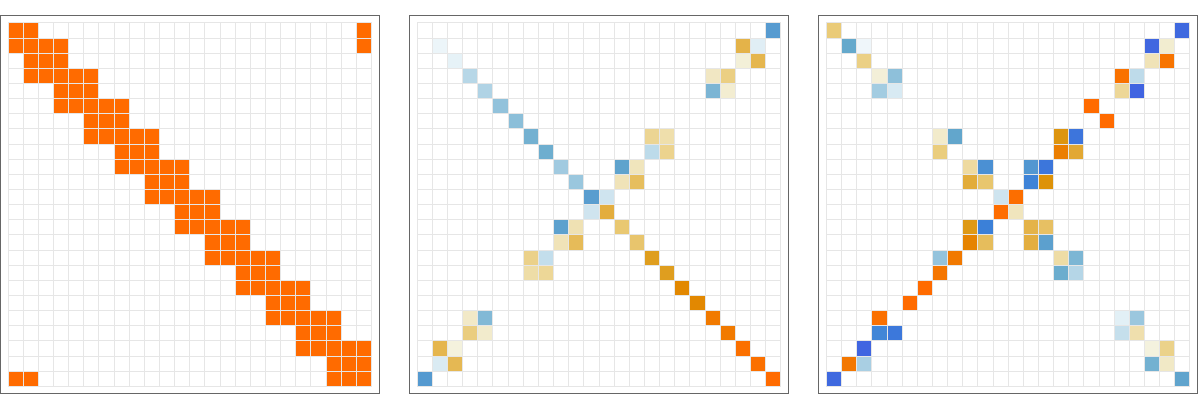
Here is a first attempt to diagonalize the connection Laplacian in the case of the circle. We first see the connection Laplacian, then after a discrete Fourier transform (which diagonalizes the Kirchhoff Laplacian). Then the eigenvectors of that matrix. The structure suggests that onecan find out explicit formulas for the diagonalization. Especially for the spectral measure for L² which has no gap any more.

[Update of January 19, 2018]: The problem of diagonalizing the Laplacian has been solved over the winter break. See This post or This article. The Blog entry shows a bit more about the struggle to solve the problem. It needed a nonlinear idea, namely to look at the transformation f(L) = L-L^-1. ]