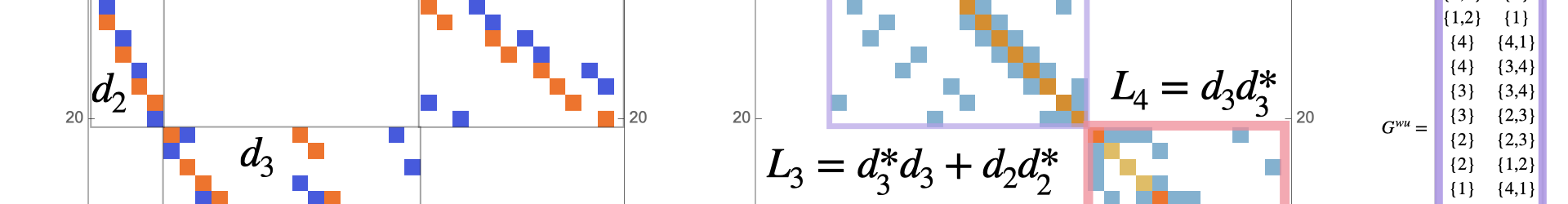My experiments so far indicate that the Wu cohomology of a d-manifold G can be read off from the usual cohomology. If is the Betti vector of G then (0,\dots,0,b_d,b_{d-1},\dots,b_1,b_0)$ appears to be the Wu Betti vector. So far, this is only a conjecture.
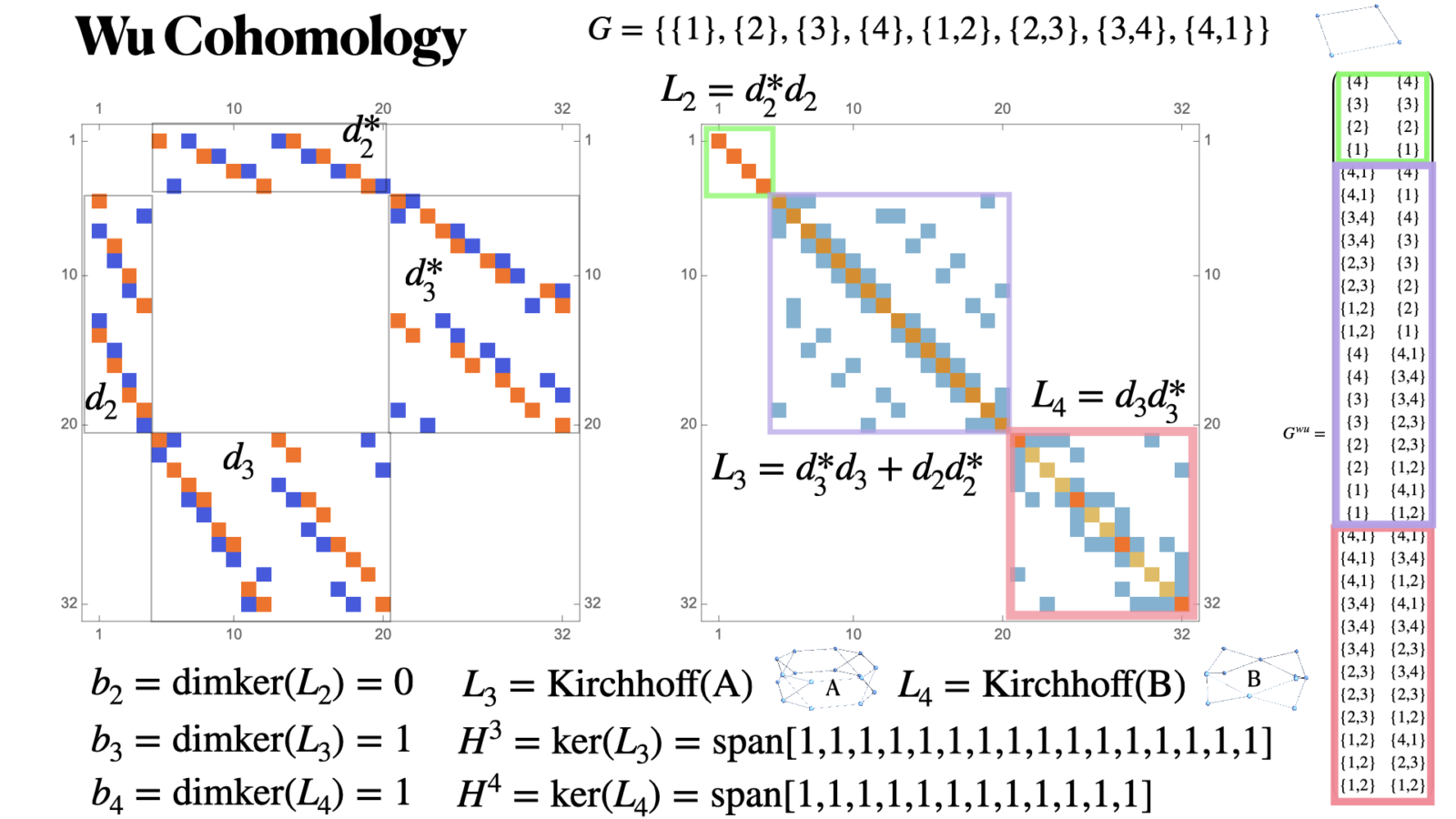
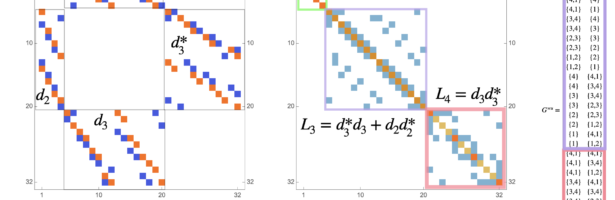
In the talk, the case , the smallest positive dimensional manifold is covered. Here is a slide showing the Wu Dirac matrix and the Wu Laplacian. The smallest dimensional sector covers the interaction of zero dimensional simplices which is not interesting. The corresponding Laplacian is diagonal. The next sector consists of discrete differential forms which deal with 1+0 dimensional parts. The Laplacian happens to be the Kirchhoff Laplacian of a graph. The last sector describes 1+1 dimensional pairs. Also the Laplacian there is a Kirchhoff Laplacian of a graph. These might just be accidents because we have such a symmetric situation. In this case
, we have
and the Wu Betti vector is
. So far, I do not see a relation. In some sense, we have to see the pairs of intersecting highest dimensional facets as points and
as the gradient which maps to functions on pairs of 0+1 dimensional simplices.