Cylinder And Moebius Strip - Quantum Calculus

[Update 3/5/2024: given that one knows now the optimal Moebius strip, one can wonder about the much easier question of what the smallest simplicial complex producing a cylinder or Moebius strip is. Below, I use in both cases 6 facets (triangles). For the Moebius strip, one can do with 5 facets and 5 points. If the complex needs to come from a graph, we need 7 points (the graph complement of C7 does work). For a cylinder, where we have 2 boundaries, we definitely need 6 triangles and 6 vertices.]

I refresh here a bit the code written in 2018 for Wu cohomology. a nice concrete cohomology. The selling point then had been that it gives different cohomology to the cylinder and Moebius strip. The Euler characteristic, simplicial cohomology as well as the Wu characteristic are the same for both spaces. For Euler characteristic and simplicial cohomology this follows from homotopy invariance, for Wu characteristic from the formula $w(G) = X(G)-X(dG)$ which holds for any manifold with boundary. Both spaces are manifolds with boundaries. They are not homeomorphic however first of all because one of them is orientable, the other not, or that the cylinder has two boundary components while the Moebius strip has only one boundary component. After last Saturday’s entry I put together the code for computing the cohomology in an independent way, also trying to make the spaces smaller. In 2018, I took simplicial complexes coming from graphs, without that we can go with 6 triangles.

(* O. Knill For the theory, see https://arxiv.org/abs/1803.06788, 2018                   *)
Generate[A_]:=If[A=={},{},Sort[Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1]]];
CleanComplex[G_]:=Union[Sort[Map[Sort,G]]];  
Whitney[s_]:=Generate[FindClique[s,Infinity,All]];  L=Length;
WuDirac[G_]:=Module[{C2,n=L[G],n2,G2={},ll,ln,d1,d2,LL2,L2,dd,b,D2},
  length[x_]:=L[x[[1]]]+L[x[[2]]]; G2={};
  Do[If[MemberQ[G,Intersection[G[[k]],G[[l]]]],
  G2=Append[G2,{G[[k]],G[[l]]}]],{k,n},{l,n}]; n2=L[G2];
  G2=Sort[G2,length[#1]<length[#2] &];ll=Map[length,G2];ln=Union[ll];
  b=Prepend[Table[Max[Flatten[Position[ll,ln[[k]]]]],{k,L[ln]}],0];
  deriv1[{x_,y_}]:=Table[{Sort[Delete[x,k]],y},{k,L[x]}];
  deriv2[{x_,y_}]:=Table[{x,Sort[Delete[y,k]]},{k,L[y]}];
  d1=Table[0,{n2},{n2}];Do[u=deriv1[G2[[m]]];
    If[L[u]>0,Do[r=Position[G2,u[[k]]];
    If[r!={},d1[[m,r[[1,1]]]]=(-1)^k],{k,L[u]}]],{m,n2}];
  d2=Table[0,{n2},{n2}];Do[u=deriv2[G2[[m]]];
    If[L[u]>0,Do[r=Position[G2,u[[k]]];
    If[r!={},d2[[m,r[[1,1]]]]=(-1)^(L[G2[[m,1]]]+k)],{k,L[u]}]],{m,n2}];
  dd = d1 + d2; D2=dd+Transpose[dd]; {D2,b}];
WuHodge[G_]:=Module[{Q,b,H},
 {Q,b}=WuDirac[G];H=Q.Q;Table[Table[H[[b[[k]]+i,b[[k]]+j]],
 {i,b[[k+1]]-b[[k]]},{j,b[[k+1]]-b[[k]]}],{k,L[b]-1}]];
WuBetti[G_]:=Module[{C2,D2,b,L2},{D2,b}=WuDirac[G]; L2 =D2.D2;
  LL2=Table[Table[L2[[b[[k]]+i,b[[k]]+j]],{i,b[[k+1]]-b[[k]]},
    {j,b[[k+1]]-b[[k]]}],{k,L[b]-1}]; C2=Map[NullSpace,LL2]; Map[L,C2]];
G1=CleanComplex[Generate[{{1,2,4},{1,4,3},{3,4,6},{3,5,6},{5,6,2},{5,2,1}}]];
Print[WuBetti[G1]]; Print["Fvector   ",Delete[BinCounts[Map[L,G1]],1]];
G2=CleanComplex[Generate[{{1,2,4},{1,4,3},{3,4,6},{3,5,6},{5,6,1},{5,1,2}}]];
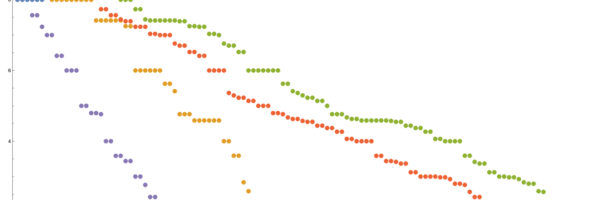
Print[WuBetti[G2]]; Print["Fvector   ",Delete[BinCounts[Map[L,G2]],1]];

Here are the eigenvalues of the Hodge blocks of Laplacian of the cylinder and the eigenvalues of the Hodge blocks of the Laplacian of the Moebius strip (to the right). One can clearly see the McKean-Singer symmetry: even and odd pairs come in pairs. Since the spaces are 2 dimensional, there are 4 Hodge blocks. The non-zero eigenvalues of the even blocks and odd blocks match up. The Moebius strip has no zero eigenvalues for the Wu Hodge Laplacian as the Wu cohomology is trivial. The matrices are 320 x 320 matrices in both cases.

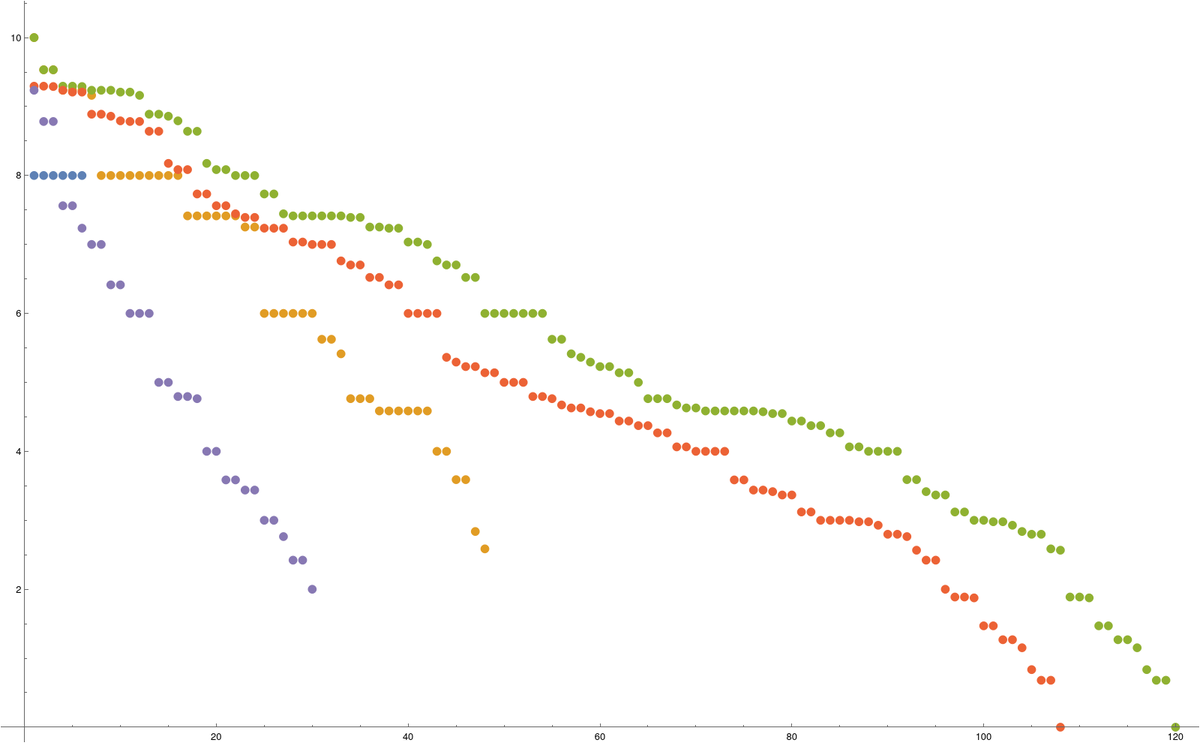
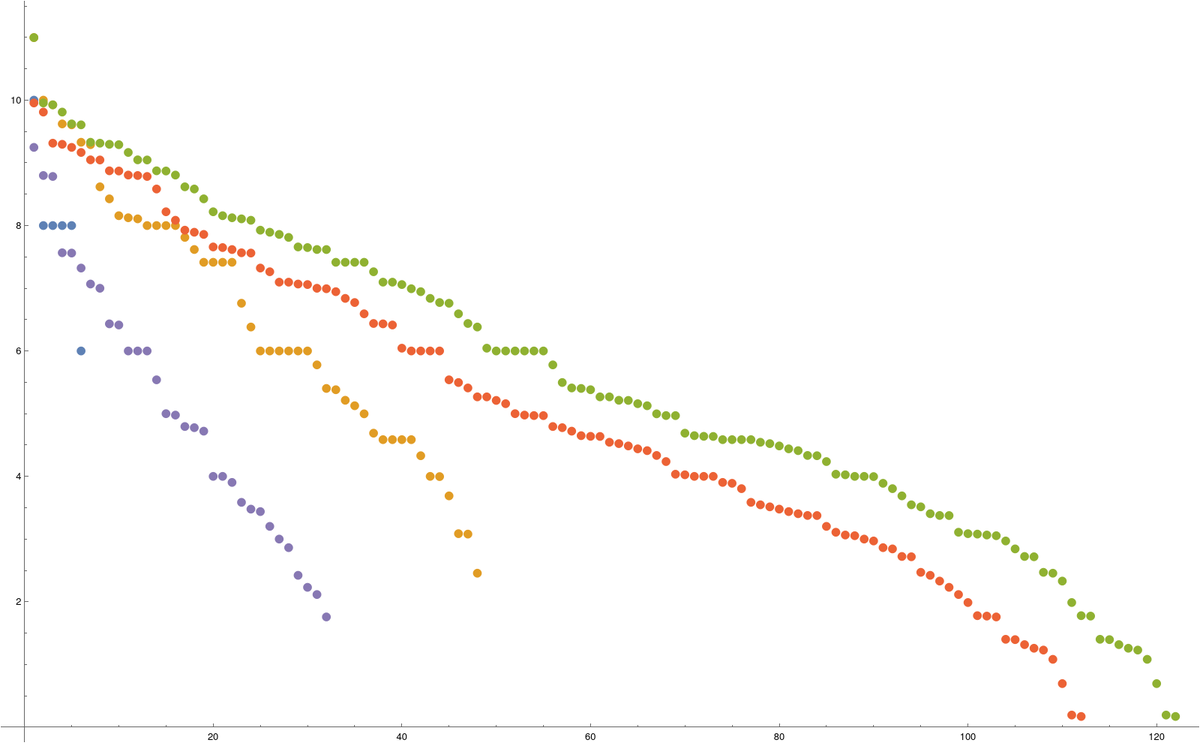
And here are the matrices

Author: oliverknill