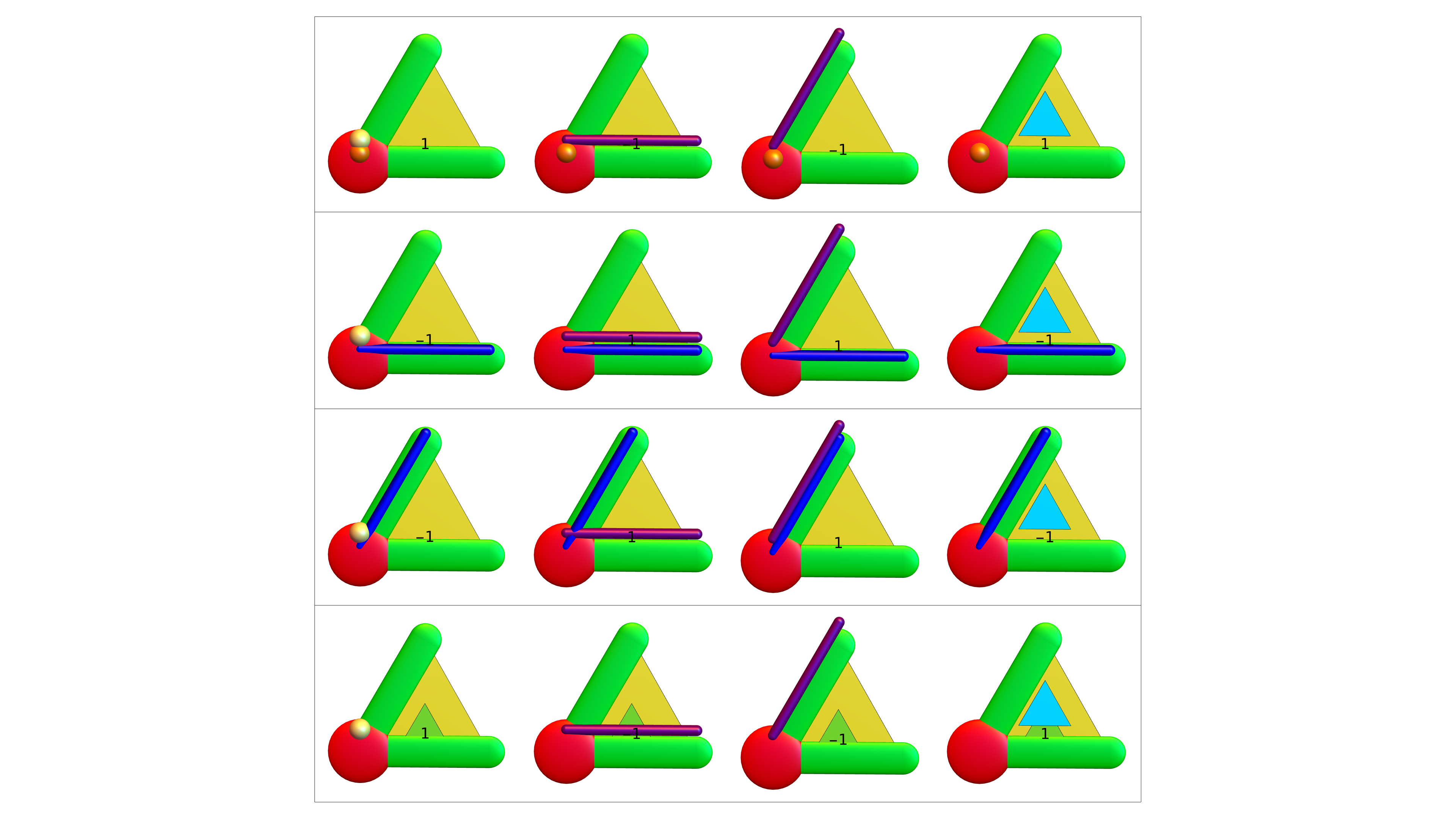
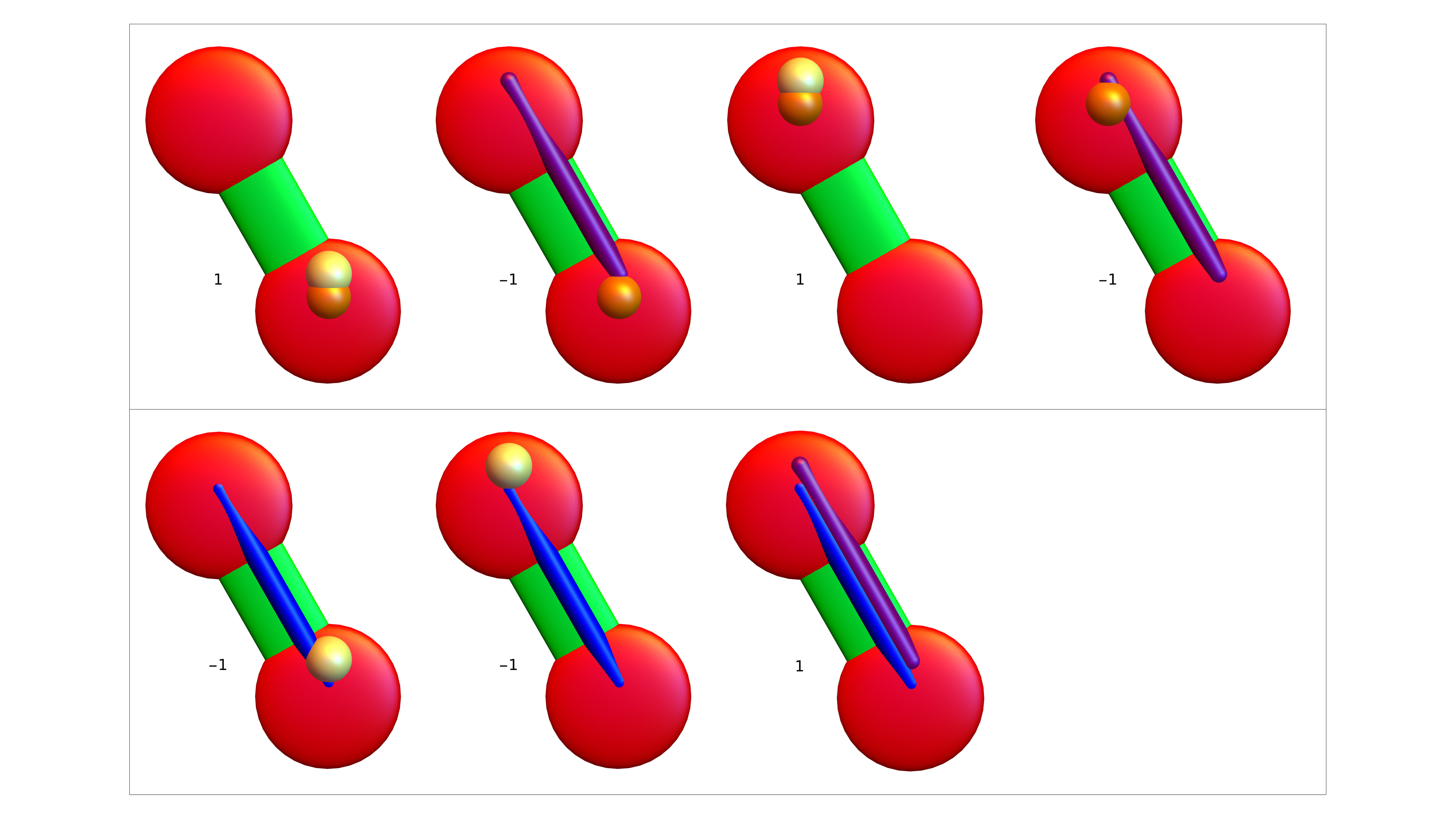
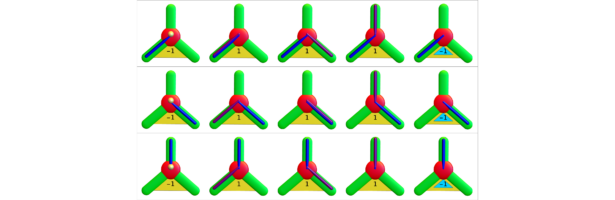
The elements of Euclid of Byrne (internet archive) are a nice example also in how to illustrate mathematics. The tools to illustrate mathematics have multiplied since Byrne’s time. Yesterday, I wanted to visualize the identity w(B(x))=w(U(x))-w(S(x)) for quadratic (Wu) characteristic which comes after linear (Euler) characteristic. In the video, the identity is illustrated for G=K2 and G=K3 where x is a zero dimensional point in each case. By the way, the identity is interesting already if x is a facet, a maximal set of dimension q in the simplicial complex. Then w(U(x))=1, and w(B(x))=(-1)^q and w(S(x))=1-(-1)^q which is the Euler Gem formula for the boundary complex of the simplex x (the (q-1) skeleton complex in a q-simplex is always a (q-1) sphere. Apropos visualization. I had tried already in January 2016 to visualize it (slides read by apple talk are here). I had then written shell (and apple talk) scripts to produce audio slides for each slide, then glued them into key note. As for this talk now, I had written a program which illustrates all the possibilites. Here is an example which is not just a simplex. We see first the unit ball B(x), then the open unit ball U(x) and finally the unit sphere S(x) (which now is a disjoint union of a K2 and K1).
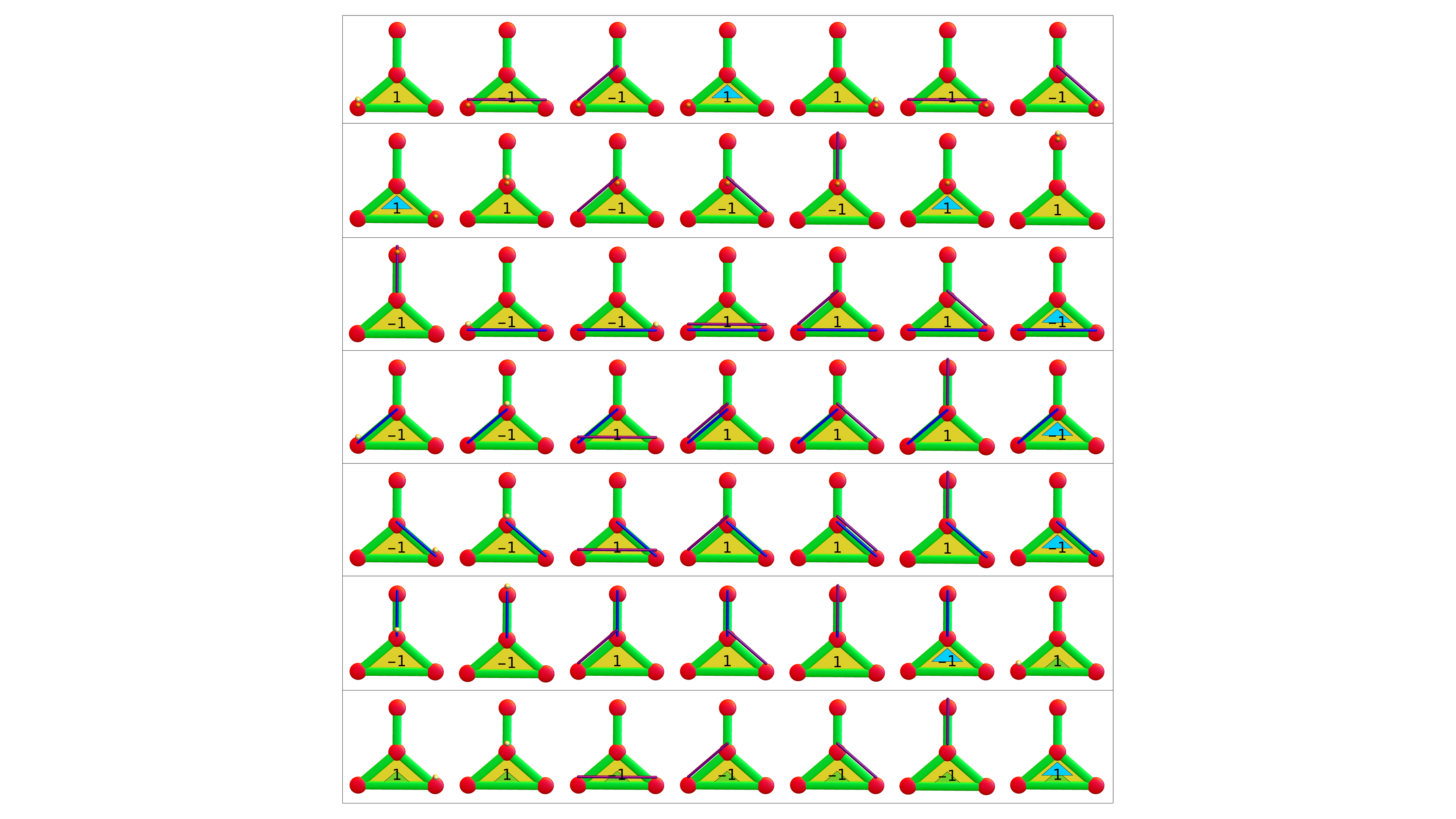
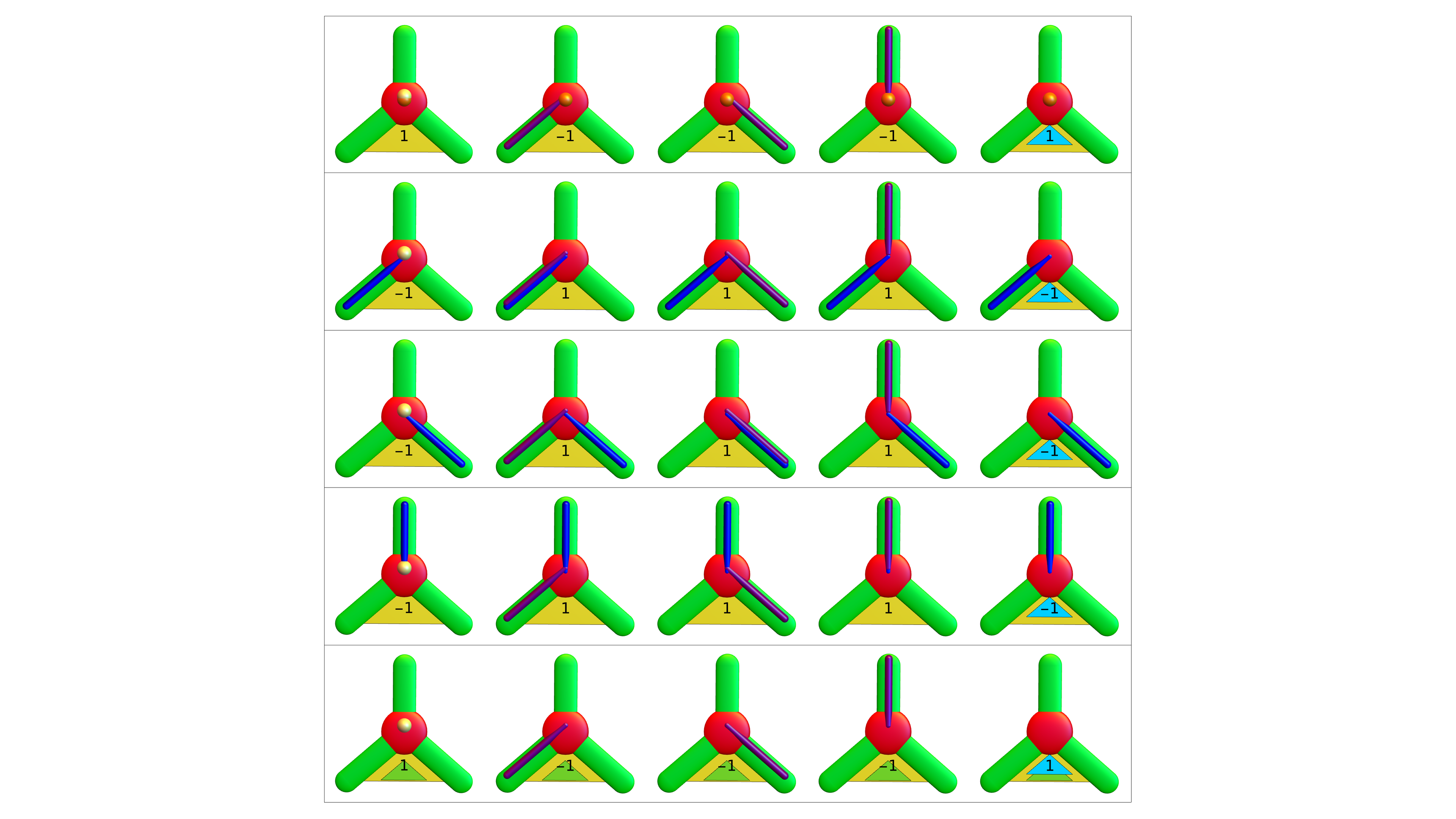
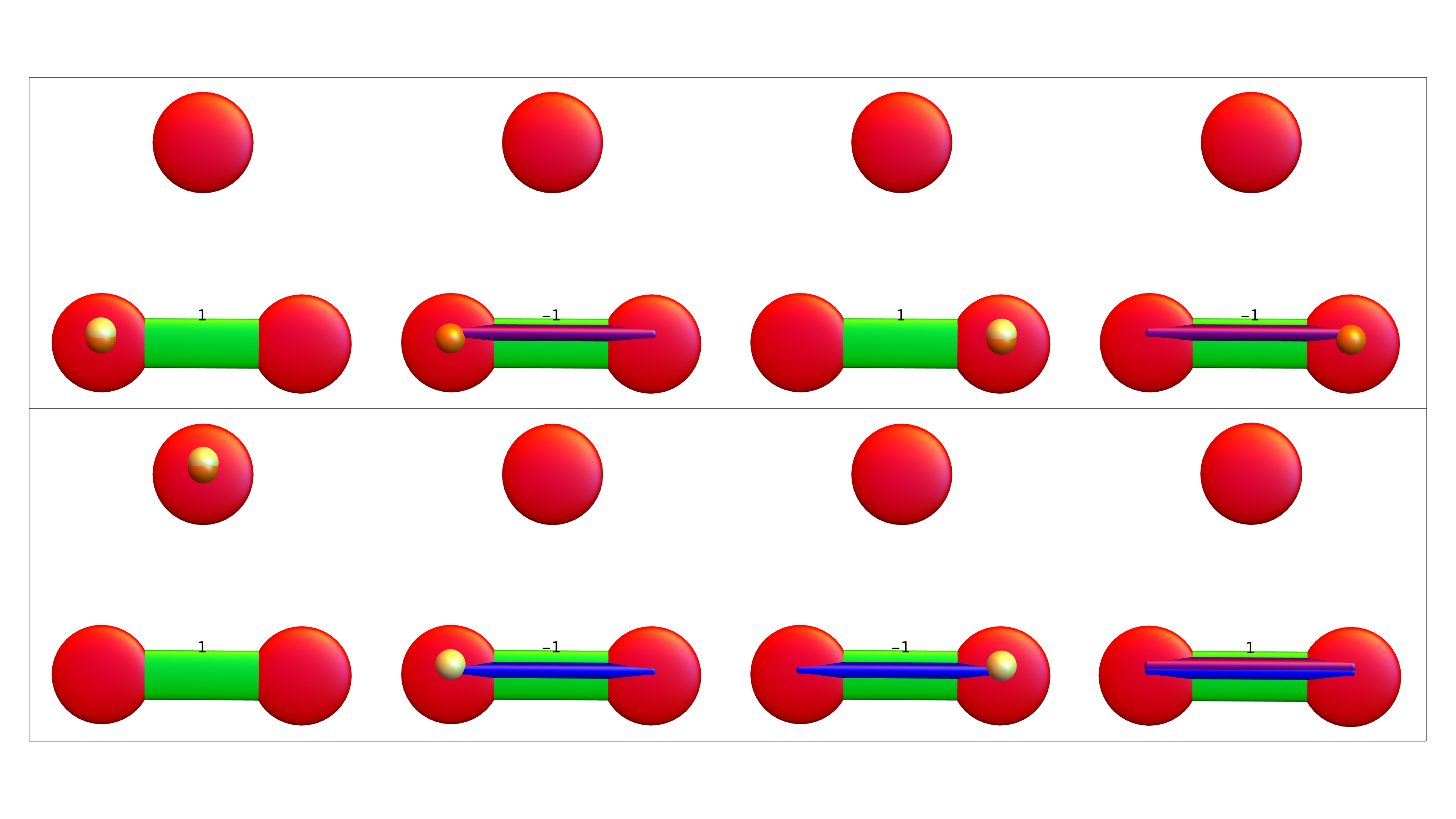
And here are the examples which were shown on the board in the case of K3. First the 37 examples for the close ball, then the 16 examples for the open ball and then the 7 examples for K2. Also here, click on a picture to see it large.