Atoms of Space - Quantum Calculus

The smallest open sets in a finite topological space form the atom of space. It was almost 100 years ago, when one has turned away from non-Hausdorff topological spaces and decided they are less relevant (Hausdorff seems have convinced Alexandrov and Hopf to focus on Hausdorff property). This is unfortunate because any finite topological space that is not T1 must be the discrete topology and so is not interesting. On a finite poset, there is a natural topology, where the upper parts or stars $U(x) = \{y, y>x\h}$ form a basis. Dual are the cores $C(x) = \{y, y<x\}$ which form the closed sets. A simplicial complex and more generally, a delta set is canonically a poset and so has a natural topology which has the correct connectivity properties. Atoms of space appear in Green functions. If L is the matrix $L(x,y) = X(C(x) \cap C(y))$ , where $X$ is the Euler characteristic $\sum_{x \in G} w(x)$ with $w(x) =(-1)^{r(x)}$ for the dimension function $r(x)$ (or a more general energy function $X(G) = \sum_{x \in G} h(x)$ ). Then this matrix L has determinant $\prod_x h(x) \in \{-1,1\}$ in the Euler characteristic case. This is the unimodularity theorem from 2016. The inverse matrix $g(x,y) = w(x) w(y) X(U(x) \cap U(y)$ involves the open sets. For simplicial complexes, L is a matrix with entries 0,1,-1 but g(x,y) can already be more complicated. The intersections of atoms U(x) and U(y) can be quite complicated in general. In 2016, I fought for several months until I got the formula for the Green functions. I had looked for a formula which involves simplicial subcomplexes and had not looked at open sets. The natural Alexandrov topology on simplicial complexes had not been yet on my mind.

An other reason for the delay in finding the Green function entries was that I read early summer 2016 the book of Mazur and Stein about Zeta functions and tried to solved one of their problems “come up with a new problem in number theory” and wrote “some experiments in number theory”. (I wrote a review about the book here on June 28, 2016). By the way, modern readers of older mathematical work often ask themselves, “why did he or she not do this and this? It would have been so easy!”, the answer is that the mathematical world is huge. You can easily get lost in a question for some time, then get distracted and travel to an other part of that big universe. Sometimes, one might be close to a solution to a problem and turn in the last moment to something else. The problem is not that there not enough problems or subjects, the problem is that there are too many things one could do. I wrote about the Green star formula on this blog here, and here (The quest). [Unfortunately, many of these early quantum calculus posts had an other latex plugin and have latex misformatted. One of the disadvantages of content management systems like wordpress is that one can not just run a simple regex command substituting all $\$Da Da Da\$$ to $\$latex Da Da Da \$$ on the entire site. ]

In 2020, I got back to the subject and worked on generalized to energized simplicial complexes and then developed Green function formulas during the winter 2022/2023 (when we were in Burlington, VT) and in 2023 to higher characteristics. We think about $g(x,y)$ as the potential energy between x and y. This makes sense as in all of mathematical physics this is the case. The gravitational or electromagnetic potential energy for example is determined by the Green function of the Laplacian of three dimensional Euclidean space, giving the g(x,y) = C/(x-y) potential.

I was looking at how much of the intersection calculus goes over to delta sets. The unimodularity theorem (as realized in 2020) works for general set of sets. Define $C(x) = {y, y<x}$ and $U(x) = {y, x<y}$ and for $A<G$ , define the energy $X(A) = \sum_{x \in A} h(x)$ . Define the matrices $L(x,y) = X( C(x) \cap C(y))$ and $g(x,y) = w(x) w(y) X(U(x) \cap U(y))$ , then $det(L)=det(g)= \prod_x h(x)$ . If the energy values are in the units of a division algebra, then g and L are inverses of each other. See the division algebra valued case paper.

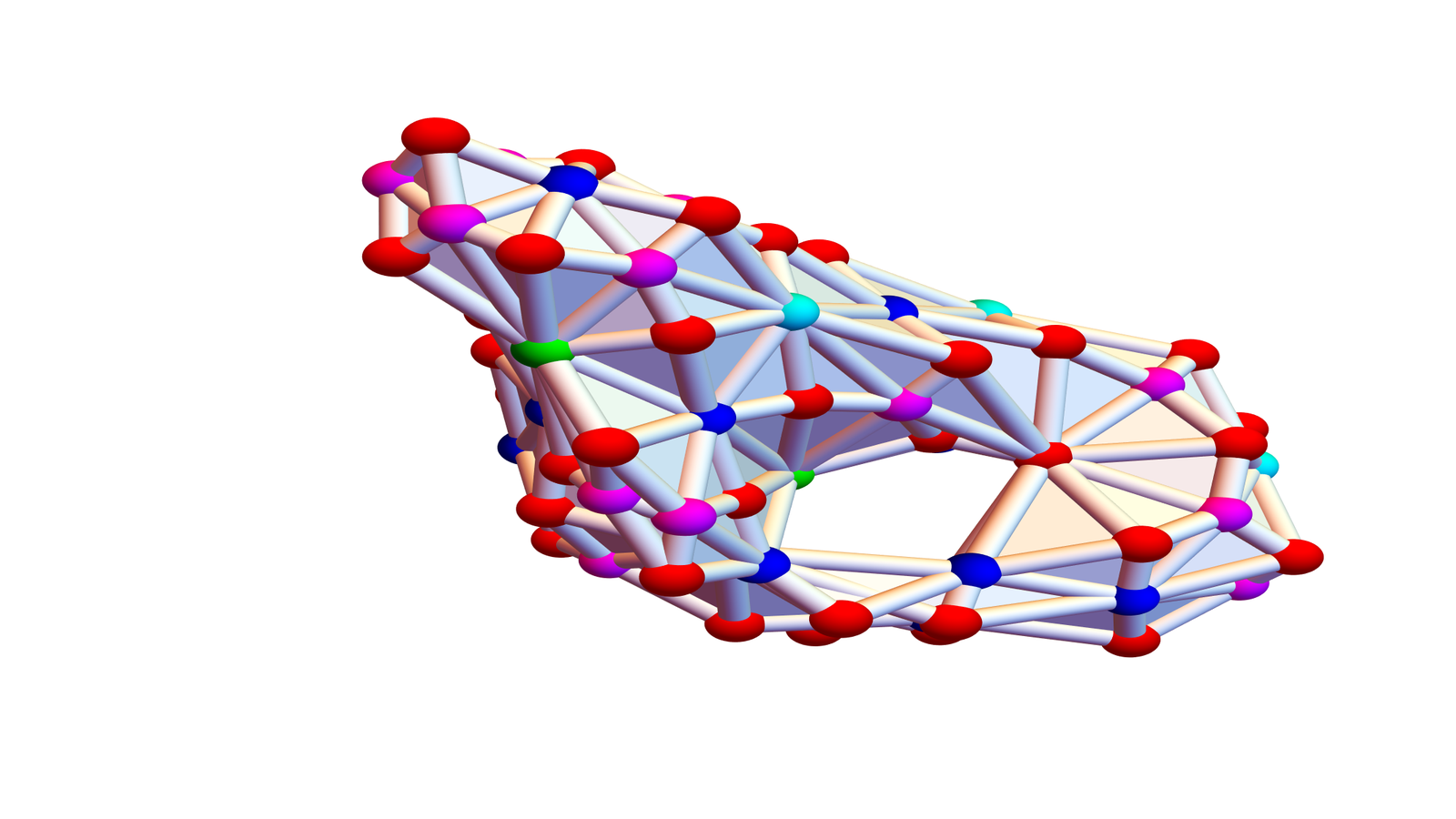
One of the reasons why talking about atoms is that an atom U(x) has the property that all its elements (simplices) are connected. Take U = { {1},{1,2}} for example. The naive connection matrix (as defined in 2016) is $\left[ \begin{matrix} 1 & 1 \\ 1 & 1 \end{matrix} \right]$ which obviously is not invertible. The better definition $L(x,y) = X( C(x) \cap C(y))$ we get $L=\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]$ and $g = \left[ \begin{matrix} 0 & 1 \\ 1& - 1 \end{matrix \right]$ . These matrices are inverses of each other and both have determinant -1. However, the energy theorem $\sum_{x,y} g(x,y) = X(G)$ does not hold. What I noticed however is that level sets in manifolds satisfy the energy theorem. They form a class of open sets (and so delta sets) where things work still. Here is an example. we take the host manifold S2xS2 which is a 4-manifold and take a random co-dimension 2 surface. In this case, it is a torus with f-vector (20,49,29). The energy theorem holds even so the manifold is not a simplicial complex. One of the quests is to find out whether in every case, we can actually realized the manifold using a simplicial complex. Note that the picture shows the Barycentric refinement. The actual complex is much smaller and has only 20 points (smallest simplices).

Author: oliverknill