Geometry of Delta Sets

Historically, geometry started in Euclidean spaces. There was no concept of coordinate when Euclid wrote the “elements”. Using “points” and “lines” as building blocks and some axioms, the reader there is lead to quantitative concepts like “length”, “angle” or “area” and many propositions and theorem. Only with Descartes, the concept of “coordinates” appeared. It is since then that we see the Euclidean plane as a product of two lines, so that each point is marked with a pair of numbers (x,y). The nomenclature “Cartesian Product” honors this discovery. When we look at finite geometries, there is the conundrum at first that producing a Cartesian product of nice manifold structures should be a manifold and that we need this product to be associative. There is no such product within the category of graphs or within the category of simplicial complexes. The set theoretical product of two simplicial complexes for example is a set of sets but not a simplicial complex because it is not closed under the operation of taking non-empty subsets. Of courses, we should not use “geometric realizations”, meaning to use the frame work of classical geometry as an escape but this defeats the purpose of the task as we want to work within a given finite category and not take something like the real line for granted.

Eilenberg and Zilber solved it the product problem in the 1950ies by inventing a new structure. The category of delta sets (semi-simplicial set), which as a functor category have products. I myself had dabbled with the question to define a product on the category of graphs such that the product of two manifolds is a manifold. [Never,ever considered graphs as one dimensional simplicial complexes but always treated them as grown up structures.] Graphs always come with a natural simplicial complex, the vertex sets of complete subgraphs. A d-manifold is a graph such that every unit sphere S(x) is a (d-1)-sphere. A d-sphere is a d-manifold such that when punctured, becomes contractible. A graph is contractible if there exists a vertex such that S(x) and G-x are both contractible. This inductive definition (essentially due to Evako from the 1990ies) solves the problem of Herman Weyl to define the concept of “sphere” and so “manifold” from within the discrete without the use of traditional mathematics. The missing part at his time had been homotopy: spheres can be characterized as manifolds which when punctured become contractible. Spheres can be characterized as category 2 manifolds. The manifold structure can be defined by the property that small r-spheres (points in distance r) are spheres. This is usually written in terms of an atlas and local parametrizations leading to various notions like topological manifolds, smooth manifolds or PL manifolds.

[ Side remark: One must remember that at the time of Weyl, one still worried about the consistency of mathematics. The “Grundlagen crisis” was seriously shaking up the believe systems of and various axiom systems for set theory were developed to get out of the mess. After Hilbert’s dream was shattered by theorems of Goedel, one has essentially lost any fear about a solid foundation of mathematics and motivation to fix it. What’s the point of worrying if we can anyway not prove that we are safe? Today, mathematicians deal with categories and universes that are not sets and do not worry. What is not considered is that it is well possible that any axiom system which deals with infinity is fundamentally flawed and inconsistent. Goedel’s theorems do not exclude that. Of course, nobody has found a problem yet, but this does not mean that it does not exist. It just put our heads into the sand and hope for the best. It might also well be that things are inconsistent, the frustration of course is that we never will nknow. [One can draw the analogy with the dangers of nuclear war. In the 50ies, one had been worried about nuclear annihilation, the horror of humanity killing itself, there had been videos like “duck and cover” pretending that there is hope in surviving a nuclear attack. The true effect would be that instead of dying within a few minutes, you might die a painful death within a few days or months essentially being tortured to death by radiation or then by violence due to the break-down of society or then starvation because of the lack of food. Today, nobody cares. We happily fight a proxy war with an other super power at the very moment and constantly feed it with more money. Polititicians even cheer and wave flags to send the billions of dollars into a foreign war.] The analog of a nuclear disaster n the mathematical foundations could come any time. It is well possible that any strong enough axiom system (essentially any axiom system we use today that involve infinity) are inconsistent. We can not prove that this does not happen, so we do not care any more. Actually, unlike a nuclear self annihilation of humanity, this would not be a complete disaster. We would just have to retrench to finite mathematics. Modern approaches to mathematics allow us to tune things and consider only finite objects. And since all we have done since is always finite, there is no problem. We should be more honest: whatever we can do when pursuing truth is finite. We can only write down finitely many symbols, process only finitely many data, triangulate out finitely many points in space, measure finitely many particles etc. Every serious computer scientist is somehow a finitist because all we do with data and algorithms is finite. Any data structure we ever can invent is finite. It is interesting that we have maybe 100 billion nerve cells in our brain and that modern AI systems have already much more “parameters” than that. We are with a tremendous speed outpacing our own brains with artificial structures, but it is still all finite. ]

Wile working on Kuenneth in Graphs I was systematically looking for a good product in graphs that preserves manifolds. The usual “cartesian product” is not useful treats graphs as one dimensional simplicial complexes. The graph Cartesian product K2 x K2 for example is a square, which is not 2 dimensional as it is does not have any triangles. We can look up the algebraic topology notes from school and think about the product as a CW complex, where we fill in the additional cells and attach them to already existing spheres inside. However, as a data structure they are not so nice. One has to give them as a dynamical object as we attach more and more cells to already existing spheres. What I came up with is not to look at the product of the vertices of the graph put to look at the product of the simplicial complexes and look at it as a graph, where the vertices are the pairs (x,y) with x,y simplices in the individual factors and where one is contained in the other. The Cartesian product of K2 x K2 is now a wheel graph with 9 vertices. As now, the product has geometric realizations that are the products of geometric realizations, Kuenneth of course holds as the product of geometric realizations is the geometric realization. But the point was to establish this in the finite and not by using geometric realizations. The products of manifolds generated like this are huge. The product is also not associative, as multiplication by 1 is already the Barycentric refinement. What I had not known then was that this is known (or equivalent) to the Stanley-Raisner product. I see it today as the Barycentric refinement of the product as a delta set. The process of Barycentric refinement brings us always again down to graphs and so simplicial complexes.

The next couple of years, I would get interested in other products, also in the relation with arithmetic. An example from 2017 or an example from 2021. When looking at arithmetic of graphs we by definition want associativity. There are various products for graphs which are associated. We have seen already the useless Cartesian product for graphs. The categorial product (small product for graphs) is also not useful because it treats graphs as one dimensional simplicial complexes: the small product of K2 with K2 is not even connected. Then there is the large product of Sabidussi which I myself also discovered by systematically looking for a product which plays together with the join operation as addition. What I had stumbled upon was the Sabidussi semi ring , where is the category of graphs, is the Zykov join and is the large multiplication. This semi ring is isomorphic to the Shannon semiring , where is the disjoint union and is the Shannon multiplication (strong multiplication). I like the Shannon ring because it has many nice properties. Kuennent holds, the product is homotopic to the Stanley-Reisner product. But many properties are a bit forbidding: the dimension does not add up as there are way too many connections. The product of K2 with K2 for example is K4, which is 3 dimensional. There is a simple homotopy however, like removing one of the diagonals to get a “discrete manifold” with boundary. While the Shannon ring is nice and says within the category of graphs, we were led to a rougher notion of “manifold” and include graphs that are homotopic to manifolds.

When computing (like computing the cohomology) in products of manifolds, we want to use as small objects as possible so that we can do computations fast or do computations after all. Especially while working on connection calculus (like Wu cohomology and energy formulas), it became clear that in order to compute the cohomology of a product manifold, we do not need to look at the simplicial complex of the graph obtained by the Stanley-Reinsner product which is much too large in general but that we can look at differential forms defined on pairs (x,y) of simplices. If G is a simplicial complex with n elements, its Dirac matrix is a matrix. When looking at the product, we can write down a Dirac matrix on the Cartesian product (as a set) . In some sense, this is already a delta set structure. We do not care any more to have a simplicial complex but care to have a Dirac operator and a possibility to keep track about dimensions. Pairs (x,y) in the product are the new “points” and should be 0 dimensional for example despite given as a pair of points like a 1-dimensional simplex connecting two points. This is absolutely no problem. If we compute with the Dirac operator of the graph, the Betti vectors just are shifted. But this is a first example, where we are forced to keep track about dimensions. It is till not yet as dramatic as in the case of say open sets, where the Dirac matrix has blocks which are empty matrices. The structure of the matrix now does not reveal the dimension. For example, if we look at a face x (simplex of maximal dimension) in a simplicial complex, then U={x} is an open set (actually the star of x). This open set has only 1 point. The Dirac matrix D is the matrix $0$. The kernel of the Laplacian is one dimensional. There is just one Betti number. If x=(1,2,3) for example in the simplicial complex K3, then the Betti vector of U is (0,0,1). The Dirac matrix of the delta set U does not show the two empty matrices for 0 forms and 1 forms. Already such simple examples show that we need not only the finite set G, the matrix D but also need the additional dimension function. That is what delta sets do with defining the set G a set of sets , where are the points of dimension k. Instead of having all these face maps and sets it is so much simpler just to talk about one set G, one matrix D and a dimension function r. When we look at level surfaces for example, we have seen that in Sard’s theorem, then the level sets are a priori defined as open sets. All we have to do however is to subtract k from the r-vector if the level set had codimension k. This is much simpler than redefining the sets and the face maps. I actually don’t know whether anybody has implemented delta sets in a computer using the face maps or in a more cumbersome way as a functor category.

When working on finite geometries, there was an other fundamental problem besides the problem of finding a good Cartesian product. It is the problem to define a good “topology” for finite sets. The first reflex of course is to look at the topology coming from a metric. It becomes clear immediately however that this is very dumb from any topological perspective. On a finite set, a metric defines the discrete topology which makes the space completely disconnected. I tried myself with Cech cover ideas, like covering the graph with open sets and look at the nerve graph. See “a notion of graph homeomorphism”. Later, I would try Zariski type topologies in which the subgraphs are the closed sets. This is actually quite close already to the solution of the problem: look at the Alexandrov topology where G is the simplicial complex of the graph and where the closed sets are the sub-simplicial complexes. This topology is a finite topology of course but it has the right dimension and connectivity properties we want. It is not Hausdorff probably the reason why non-Hausdorff topologies have been overlooked (as being relevant) for decades. In the case of the Zariski topology one can justify that it is maybe not that good because there are too many open sets there, but on a simplicial complex, the structure is perfect. It especially plays well with cohomology. Open sets also come with a Dirac operator and so are delta sets and notions which are cumbersome in the continuum are just much more elegant in the finite. If (K,U) is a closed-open pair in G, meaning K is closed and U is open and K,U are disjoint with union G, then we can investigate the relation between the cohomology of K and U. There are many ways to think about this, and one way is to think of K as a closed laboratory and U the environment outside. If we think about cohomology classes as “particles”, then the isolated system (K,U) has together more or an equal amount particles than the joined system. The prototype is to look at a closed ball G and look at the boundary K whicih is a sphere and the interior U which is an open ball. Now the cohomology of G is (1,0,0…,0) and the cohomology of K is (1,0,…,1,0) and the cohomology of U is (0,0,…,1). We see that the fusion merges the volume form on U with the volume form on K. We can think of the 1-point compactification of U again as a sphere with cohomology (1,0,…,0,1). The topological frame work allows to say in a very convenitent way what the quotient G/K is.

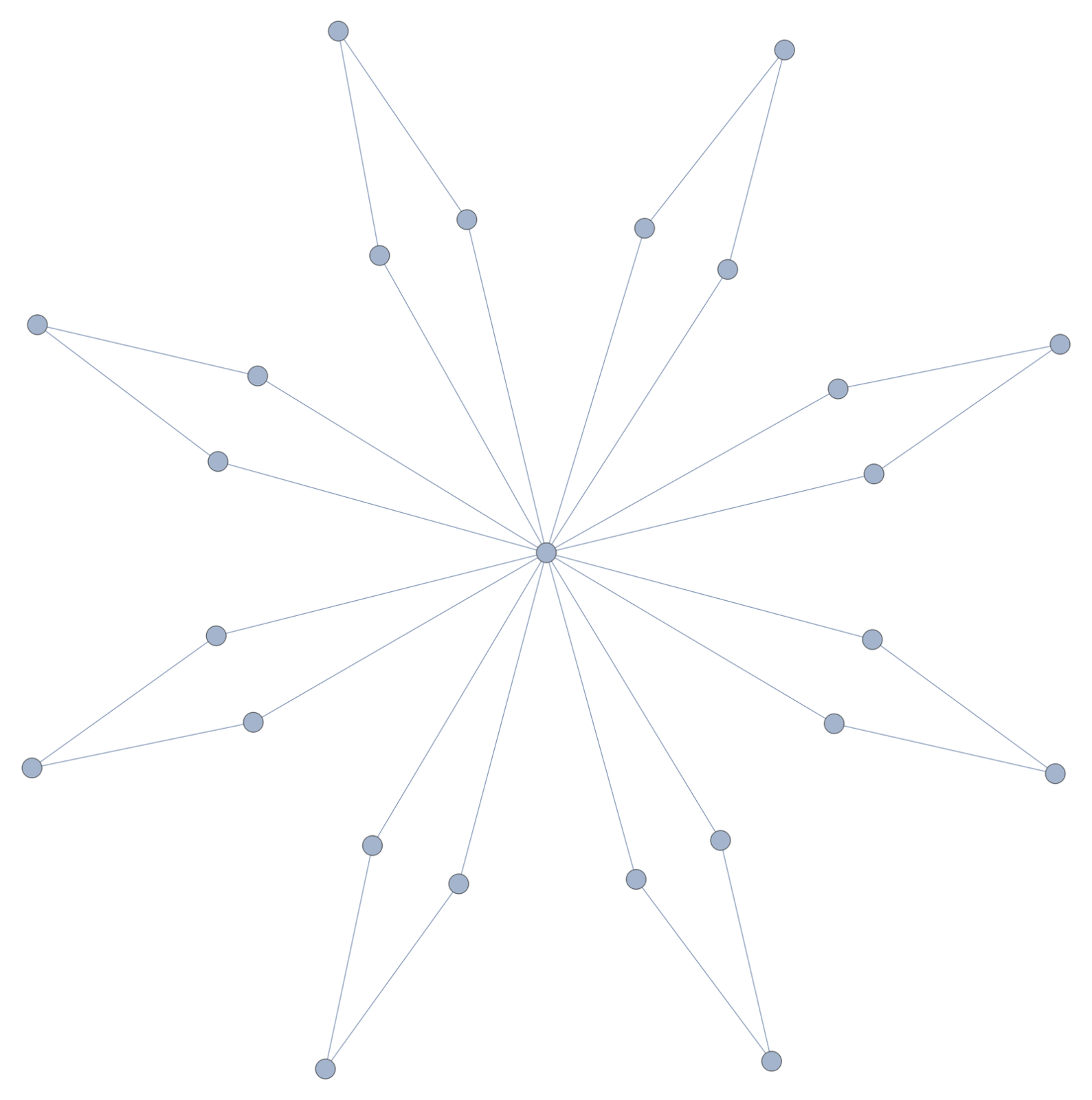
Lets look at an other example (not mentioned in the talk). Lets start with the second Barycentric refinement of the star graph with 7 rays. (Mathematica s = ToGraph[Whitney[ToGraph[Whitney[StarGraph[7]]]]];) It of course has Betti vector (1,0) as it is contractible. Now look at K, the 0-dimensional subcomplex formed by the center node and the leaves (the boundary nodes with one neighbor). K of course has cohomology (8,0) as it consists of 8 points and nothing else. The complement U now consists of 7 open intervals with cohomology (0,7). Now b(U)+b(K)=(8,7) which is much larger than b(G)=(1,0) but merging kills 7 particle pairs. Now lets look at G/K which is the 1-point compactification of U. We get a Bouquet of circles. If we would have done that with the star graph rather than with the second Barycentric refinement, we would get a quiver (a 1-vertex graph with 7 edges.