Incidence and Intersection
Graph theory

Incidence and Intersection

 , ,

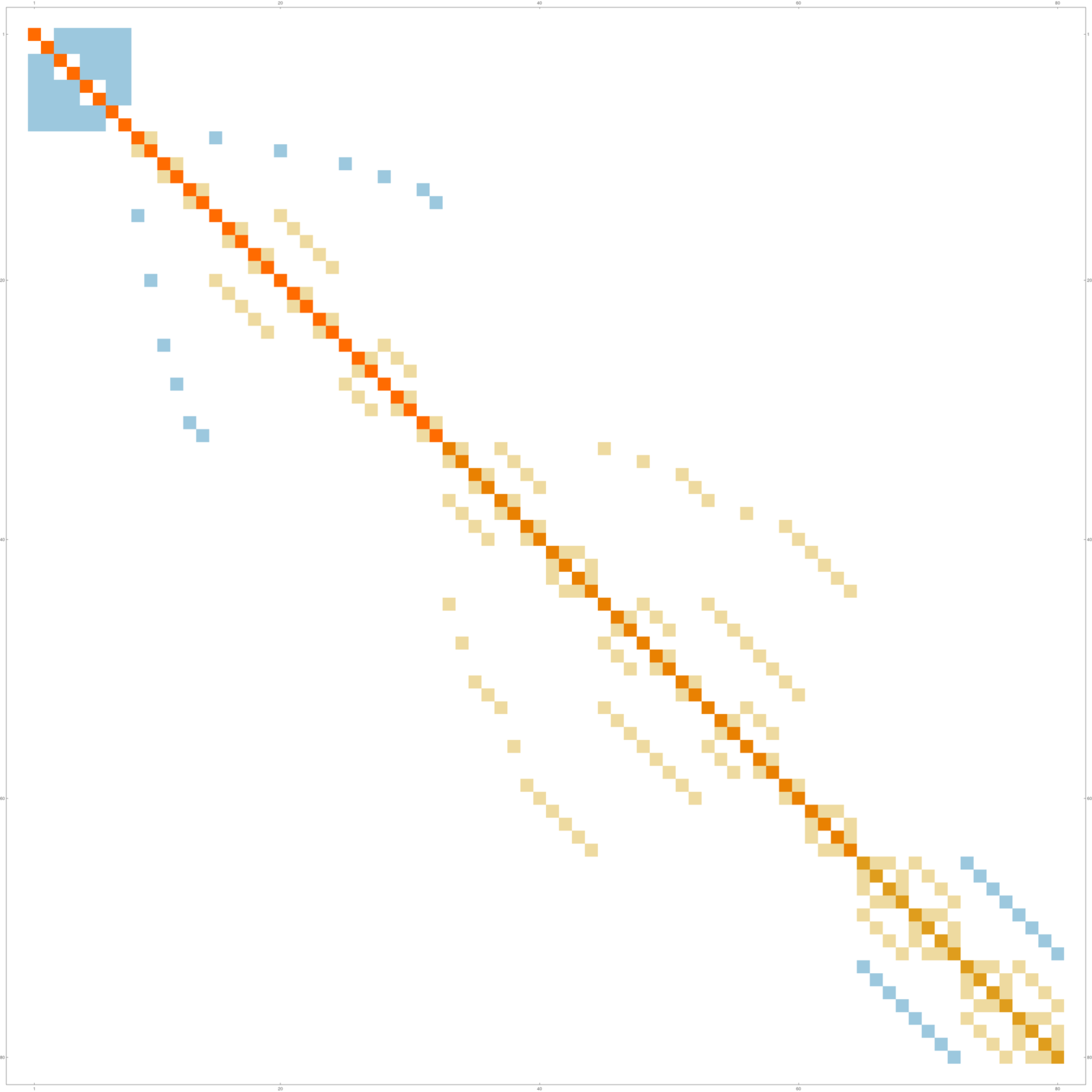
Barycentric and Connection graphs

Barycentric graphs depend on incidence, connection graphs on intersection. Here are some examples from this blog. Both graphs have as the vertex set the complete subgraphs of the graph. In the connection graph, we take the intersection, in the Barycentric case, we take incidence. Here are two pictures illustrating this. Our initial graph is a 3-sphere, the join of two circular graphs C_4. The Graph s has the f-function 1 + 8 x + 24 x^2 + 32 x^3 + 16 x^4 with 80 vertices.

  • Barycentric Refinement
  • Connection Refinement

Here is the Hodge Laplacian and the connection Laplacian: The Hodge Laplacian H is a direct sum of form Laplacians, the connection Laplacian is invertible and has here determinant 1.

  • The Shannon product of two linear graphs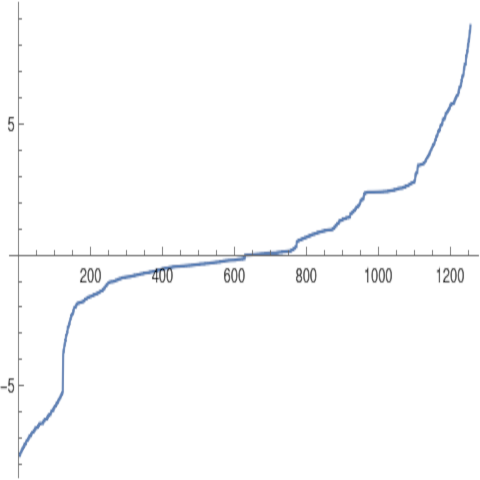
  • The spetrum of the inverse of the connection Laplacian of this graph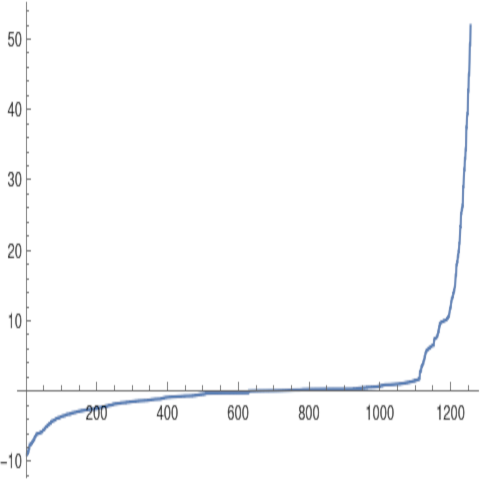
  • The spectrum of the connection Laplacian of this graph.
The minimal absolute eigenvalue of the connection Laplacian is 0.11435, the maximum 52.0261. There is a spectral gap which does not get smaller even in the van Hoove limit! Also for the infinite Laplacian, we have stability of the vacuum. Apropos Statistical mechanics, the Shannon product of two linear graphs is the most common neighborhood graph considered in statisticsal mechanics. The unit sphere is the set of lattice positions, which a king can move to. It is technically a three dimensional graph because of the presence of tetrahedra graphs (3 dimensional simplices). BUt the graph is a soft 2-manifold. All unit spheres are soft 1-spheres. Note that when taking the connection Laplacian of the graph L(20) x L(20) , we already have a matrix with 3687 entries. In that case, the minimal absolute eigenvalue is 0.11311 and the maximal absolute value 53.2093. There is a limit.

Frenkel-Kontorova

The Frenkel-Kontorova model in nonlinear physics is a general variational problem. If \Delta is a Laplacian on a graph and U a real valued potential, one can look the functional E[ (u,\Delta u)/2 + \epsilon U(u) ], where E is an expectation on some linear space of functions and \epsilon is a perturbation parameters. Critical points satisfy a non-linear system $\Delta u+\epsilon V(u)=0$,, where $U’=V$. These are called the Euler equations. Unfortunately for physics, the Laplacians we usually deal with are singular in the sense that their inverse, the Green functions are unbounded. The source of the problem exists already in the simplest cases like if space is a finite graph, where Laplacians have a kernel. They are calledHarmonic forms. The Laplacian of a space determines the natural Newton potential on the space and that is always singular. In the most famous case when space is \mathbb{R}^3, we see the 1/r potential like in gravity or in electro-magnetism. But it is obvious that this can not make sense also physically: take two neutral elements like neutrons hitting each other front on, their gravitational energy would go to infinity. We know that there are quantum effects but still, even relativistic mathematics breaks down. This touches of course to the fundamental question how to combine gravity with quantum mechanics but it is clear that classical force descriptions will change fundamentally in the very small. As mathematicians, we see the difficulties in mathematical variational problems like how to describe critical points of the above variational problem if the non-linear perturbation has been turned on. This can already be subtle in the very simplest cases like when space is the set of integers \mathbb{Z} and \Delta u(n) = u(n+1)-2 u(n) + u(n-1) and U(u) = \cos(u). The fact that \Delta is non-invertible can be seen that \Delta has the constant functions as kernel. Now, of course, the variational problem depends on the Banach space which is chosen. A good one is to fix some real \alpha and to take C(\mathbb{T}) and take for a function q in that Banach space the random sequence u(n)=q(x+n \alpha), where x in the circle is an element in the probability space we integrate over to get the expectation. The functional to minimize is then \int_{\mathbb{T}} (q(x+\alpha)-q(x))^2/2+ \epsilon \cos(q(x)) \; dx and critical points satisfy the nonlinear equation q(x+\alpha) - 2 q(x) +q(x-\alpha) = \epsilon \sin(q(x)). Critical points correspond to invariant curves (KAM tori) of the Standard map. Solving such nonlinear equations in a Banach space is a KAM problem. It needs a sophisticated implicit function theorem to be solved in a Banach space of real analytic functions and only has solutions if \alpha is sufficiently Diophantine. It does not really matter much what Frenkel-Kontorova model we chose, also whether it is higher dimensional or not. The important thing to realize is that the problem to continue solutions from c=0 to c>0 is hard and only works for carefully crafted solutions in the case c=0 (which can be established by looking at configurations u(n) defined by a specific dynamical system like an irrational rotation. The source of the problem is that the Hessian, the linear operator obtained by linearizing near the equilbrium solution is not invertible. If it were invertible, we could continue the solution using the soft implicit function theorem. For more about the calculus of variations, check out the book of Moser. The problem of non-invertibility of the Laplacian \Delta when looking at non-linear equations \Delta u + V(u)=0.