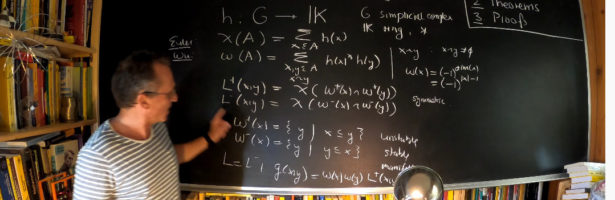The results mentioned in the slides before are now written down. This document contains a proof of the energy relation . There are several reason for setting things up more generally and there is also some mentioning in the article: allowing general rings and not just division algebras extends the frame work to operator algebras for example. But one does not have to stop there. One can also look at rings of geometries extending our usual arithmetic. This allows to see the determinant as an exponential map on that arithmetic. A second reason why generality helpe, is that the proofs have become simpler. Looking at the story algebraically and not filling in any concrete ring elements but take polynomial rings also makes the proofs easier. To prove an identity, we only have to compare coefficients. This is by far a new idea. In the talk, I mention briefly also Stanley-Raisner rings, which also purely algebraically encode complexes but here it is much simpler. Rather than encoding a triangle with vertices a b c with the polynomial element a b c as done in Stanley-Raisner rings, we just write x for the triangle. The triangle is a point in the simplicial complex. Here is a presentation from October 14, 2020: [P.S. The story of Ernst Ising is very interesting. His PhD work had been advised by Wilhelm Lenz and was published in 1925. It made Ising famous. There are now thousands of articles dealing with that model. I have heard in the mathematical physics and statistical mechanics community,that there is there also some satisfaction in spelling Ising willfully in the wrong way and not the German way. It brings some justice to the fact that Ising got so much credit for so little work. There are also rumors that there was a reason why he did not publish any more: keeping track and collecting the fame from his model absorbed and occupied him until his 98th birthday. I do not know whether that is true, but it is a good story.]