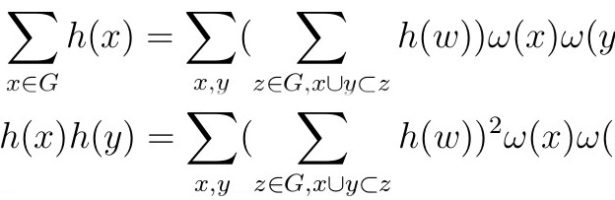Energy relation for Wu characteristic

Introduction

Before discovering the fact that connection Laplacians of simplicial complexes are unimodular (a result which was important enough to be sent in for publication), I had been working on Wu characteristic, which is a multi-linear valuation of Euler characteristic. Much of our standard mathematics and calculus is concerned with Euler characteristic: theorems like Poincare-Hopf, Riemann-Roch, Gauss-Bonnet, McKean-Singer, Brouwer-Lefschetz, Riemann-Hurwitz, Euler-Poincare, Poincare duality, Atiyah-Singer are outposts of this. Here is a math table talk illustrating this. All these theorems have discrete versions which are combinatorial and simpler than the classical theorems. Indeed, most of these relations are refreshingly non-technical while in classical settings one has to worry about technicalities like elliptic regularity or smoothness or degenerate cases. As they are universal in the discrete in the sense to work with minimal assumptions they are also easier. For the energy relations we are going to look at here, we need G to be a finite abstract simplicial complex, a finite set of sets which is invariant under the operation of taking finite non-empty subsets.

Update October 4: some slides mentioning this already

Wu characteristic $\omega(G) = \sum_{x \sim y} \omega(x) \omega(y)$ is a quadratic analogue of the Euler characteristic $\chi(G) = \sum_{x \in G} \omega(x)$ for a finite set of sets $G$ . It sums over all pairs $x,y$ of sets which intersect. After discovering the relation $\chi(G) = \sum_{x,y} g(x,y)$ summing up all potential energies g(x,y) of the Green function of the connection Laplacian $L$ , I had in vain been looking for an analogue for Wu characteristic. Is there one at all? When experimenting with new things in mathematics, one never knows whether there is something to be found. A couple of days ago, I finally stumbled upon a Wu characteristic analogue of the energy relation for Euler characteristic. Of course, one looks first in the simplest case, when we have the topological set-up with energy function $\omega(x)=(-1)^{dim(x)}$ , where the Euler characteristic is the classical Euler characteristic and where Wu characteristic is the Wu characteristic which is topological in that it agrees with Euler characteristic for closed discrete manifolds. The new relation is $\omega(G)= \sum_{x \sim y} \omega(x) \omega(y) = \sum_{x,y} g(x,y)^2 \omega(x) \omega(y)$ . The Green function matrix is $g(x,y) = \omega(x) \omega(y) H(W^+(x) \cap W^-(y))$ with $W^+(x) = \{ z \in G, x \subset z \}$ . The connection matrix is $L(x,y) = H(W^-(x) \cap W^-(y))$ . Note that on the right hand side of the new relation, we are summing over all pairs and not only intersecting pairs. They still have to be close so that the unstable manifolds intersect. I had not noticed see this before but must have been very close, as I had experimented with moments $\sum_{x,y} g(x,y)^2$ of the Green function entries and even asked about interpretations about them as they look a bit like the variance analogue of expectation. As in statistics, covariance matrices play an important role similarly as expectations of random variables do.This happens also here, the Euler characteristic is some sort of energy expectation and Wu characteristic is some sort of energy variance. A bit unsurprisingly, it was important to look at “super” entries $\omega(x) \omega(y)$ . This checkerboard sum over all matrix elements plays the role of the super trace in a Hilbert-Schmidt setting. The energy theorem $\chi(G) = \sum_{x,y} g(x,y)$ had been proven via the McKean-Singer relation telling that the super trace of g is the Euler characteristic and was already not totally obvious. It is related to a discrete version of the classical McKean-Singer result that the super trace of the heat kernel of the classical Hodge Laplacian on a compact smooth manifold is the Euler characteristic $str(e^{-H t}) = \chi(M)$ for compact Riemannian manifolds a relation which also holds in the discrete. The Hodge McKean-Singer story is a bit easier as for the Hodge Laplacian, one has the Dirac operator which produces the symmetry between even and odd dimensional sectors of differential forms. McKean Singer is one of the key ingredients why Atiyah-Singer works, there is a symmetry between non-zero spectrum of even and odd dimensional sectors. The harmonic part, then usually has its symmetry broken producing an index which in the simplest case is Euler characteristic, the dimension of the even dimensional harmonic forms minus the dimension of the odd-dimensionsal form. It is much less surprising in the discrete as in the continuum, the Fredholm miracle of having a finite index happens even if the Laplacians do not work on finite dimensional Hilbert spaces.

Here is the Mathematica code (used for the discovery of the new energy relation for Wu characteristic). It generates a random complex, a random energy function (called e here) and then computes the matrices L,g, the Wu characteristic of this energy and then the super-duper checkerboard trace of the Green function squares. That also works in the complex, where we take the first entry complex conjugate. In that case, Wu characteristic is real. In the case when h(x) are operators in an operator algebra like a C* algebra, then the Wu characteristic is a self-adjoint operator. In the case when the algebra has a finite trace like for a type II von Neumann algebra, then one can also take the trace of the identity on both sides and get identities for numbers. As in this entire connection frame work, it is just fantastic to have bounded finite range Green functions, something which just produces a lot of problems in classical physics, when looking at the Hodge story. Of course, both frameworks are important, the Hodge story leading to cohomology and sometimes (like one dimensional complexes, one can relate the Hodge and the connection story). The Hodge story is also the covering most of the classical physics as 2-forms are fields and vector potentials are 1-forms and scalare fields are 0-forms. So far, the connection story has not much physics in it except that it produces interesting structures which can be explored experimentally and which one can quantify by physical laws which then can be compared with the experiments (which is what physics is about).

(* Oliver Knill, September 20, 2020,  Mathematica Code for Wu Energy theorem  *)
Generate[A_]:=Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1];
RandomSets[n_,m_]:=Module[{A={},X=Range[n],k},Do[k:=1+Random[Integer,n-1];
                   A=Append[A,Union[RandomChoice[X,k]]],{m}];Sort[Generate[A]]];
G=RandomSets[6,12]; n=Length[G]; e=Table[Random[Integer,6]-3,{n}]; 
energy[A_]:=If[A=={},0,Sum[e[[Position[G,A[[k]]][[1,1]]]],{k,Length[A]}]];
T[kk_,ll_]:=If[Greater[Length[Intersection[G[[kk]],G[[ll]]]],0],1,0];      
S=Table[-(-1)^Length[G[[k]]]*If[k ==l,1,0],{k,n},{l,n}];w=Table[S[[k,k]],{k,n}];
star[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[v,x],u=Append[u,v]],{k,n}];u];
core[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[x,v],u=Append[u,v]],{k,n}];u];
Wminus     = Table[Intersection[core[G[[k]]],core[G[[l]]]],{k,n},{l,n}];
Wplus      = Table[Intersection[star[G[[k]]],star[G[[l]]]],{k,n},{l,n}];
Lminus     = Table[energy[Wminus[[k,l]]],    {k,n},{l,n}];  L  =      Lminus;
Lplus      = Table[energy[Wplus[[k,l]]],     {k,n},{l,n}];  g  =   S.Lplus.S;
S0=Tr[S.g.S.g];                     (* Energy Theorem for Wu Characteristic   *)
S1=Simplify[Sum[w[[k]]*w[[l]]*g[[k,l]]^2,{k,n},{l,n}]];   (* Checkerboard sum *)
S2=Simplify[Sum[e[[k]]*e[[l]]*T[k,l],{k,n},{l,n}]];           Print[{S0,S1,S2}];

Let me just write down those relations for the set of sets G in the case when we have an complex-valued function $h: G \to \mathbb{C}$ , which energizes the complex. An algebraic geometer would see this in the integer case also as a divisor. It is in theorems like Riemann-Roch, where one looks at such energized Euler characteristics as one considers there the sum of the Euler characteristic and the degree of the divisor. Now $\chi(G) = \sum_{x \in G} h(x)$ is the energized Euler characteristic and $\omega(G) = \sum_{x \sim y \in G} h(x) h(y)$ is the energized Wu characteristic. One can see it as an Ising type rsp Heisenberg model type interaction depending on the division algebra used. If $h$ takes values in the quaternion algebra, then the interaction has a 3D Heisenberg type flavor, but it is purely geometrical: we sum up just deterministic pair correlation energies over intersecting sets in G. One could however then look at all possible energies and average over them. In the following, we have to assume that G is a simplicial complex, a finite set of sets closed under the operation of taking finite non-empty subsets. In a statistical mechanical setting, one usually looks a lattice and look at all possible fields h and use the probability space to generate some macrosopic quantities which are interesting. The statisticians then play the game of taking infinite volume limits. Here, in a topological setting, where we do not assume any lattice structure (actually we do not assume anything except the simplicial complex structure for the finite set of sets), the Barycentric refinement limit offers itself as a natural van Hove limit replacement. In that case, because of general principles showing that only the largest dimensional parts matter and lower dimensional interface energies do not matter asymptotically, one has limiting quantities which only are dimension dependent and do not depend on the structure of G at all. I demonstrated a couple of years ago that the density of states of operators like the Kirchhoff Laplacians $H_0$ , (the zero dimensional part of the Hodge Lapacian $H=(d+d^*)^2$ ), converges to a universal limit. That also works for the full Hodge Laplacian (which includes the Laplacians $H_k$ on other form sectors) or connection Laplacias and the proof is the same (just a Lidskii perturbation lemma is needed to estimate what happens if the Barycentric division is replaced by a disjoint union). Now, any quantitity which is measured locally has a universal limiting value, universal in the sense that it does not matter what simplicial complex we start with as long as the maximal dimension is fixed. Again, a statistical mechanics person would introduce quantities which depend on temperature or inverse temperature and then look how the infinite volume limit depends on that parameter. Discontinuities or discontinuities in some derivative then are called phase transitions.

The linear energy theorem told that (even in this more general energized context) that $\chi(G) = \sum_{x \in G} h(x) = \sum_{x,y} \omega(x) \omega(y) ( \sum_{z, x \cup y \subset z} h(w))$ . The new quadratic version tells also more generally now for division algebra valued functions that $\omega(G) = \sum_{x \cap y \neq \emptyset} h(x) h(y)$ agrees with $\sum_{x,y} \omega(x) \omega(y) ( \sum_{z , x \cup y \subset z} h(w))^2$ (a sum which does not assume that the pairs x,y intersect but only that their unstable manifolds intersect in the sense that they are contained in a common set). As for now, this is only an experimental realization. I have some idea how hard it will be to prove this, because I I suspect that the path which worked in the linear case (Euler characteristic) works also in the quadratic case (Wu charactristic). For the energy relation for Euler characteristic I had used the Poincare-Hopf-Gauss-Bonnet type result and seen the McKean-Singer relation as a result in which the potential energy at a point x is equal to a curvature which sums up to Euler characteristic. I suspect it only takes a few days to prove the relation but I had been wrong before in estimating the time to prove things. The unimodularity result about the determinant of L needed several months (I needed to extend the result first to CW-complexes in order to make induction) and finding the formula for the inverse of L took also several months and lots of experimentation partly due to the fact that the unstable manifolds $W^+(x) = \{ z \in G, x \subset z \}$ are no more simplicial complexes in general, unlike the stable manifolds $W^-(x) = \{ z \in G, z \subset x \}$ which by definition are closed under the operation of taking non-empty subsets. There is obviously a structural asymmetry between L and g even-so the operators are defined very similarly. In the Green function case, we also deal with arbitrary set of sets (multi-graphs, a structure without any axiom) and not only simplicial complexes (a structure with one axiom).

In the case of Wu characteristic, there is a cohomology which works similarly as the classical simplicial cohomology works for Euler characteristic. This cohomology is more sensitive and no more homotopy independent, it can distinguish the Moebius strip from the cylinder for example. I had also developed Gauss-Bonnet and Poincare-Hopf results. It is most likely that the new energy relation is a consequence of Gauss-Bonnet again: when summing over one variable x, one gets some sort of Wu curvature which then when summed over the other variable is the Wu characteristic. The first of the half year in 2020, I had worked also in very classical differential geometric set-ups where one also has a lot of freedom to construct curvatures. This certainly is also true for Wu characteristic, which so far has no analogue in the continuum. Except that I know for geometric discrete manifolds with boundary that the Wu characteristic is the Euler characteristic of the entire manifold with boundary minus the Euler characteristic of the boundary. Wu characteristic becomes really interesting when we deal with geometric structures which are no more manifolds, like for example varieties or other so called stratified spaces. There are then interesting curvatures which appear at the singularities. See this blog entry about Wu characteristic.

About connection calculus.

Let $G$ be a finite set of non-empty sets and $h: G \to \mathbb{C}$ a complex valued function. We look at this as an “energized geometry”. A physicists would look at h as a quantum wave function, in algebraic geometry, if the function is integer valued one would see this as a divisor. For a subset $A \subset G$ , one can now define the energy $H(A) = \sum_{x \in A} h(x)$ and especially $H(G)=\chi(G)$ of the entire space. If $h(x) = (-1)^{{\rm dim}(x)}$ then $H(G)$ is the Euler characteristic of G. This is very important special case because it is involved in most of classical mathematics we learn when becoming mathematicians. Now, any finite set of sets has an order structure and so also a natural hyperbolic structure. The stable manifold $W^-(x)$ of a set x is the set of sets in G which are part of x and the unstable manifold $W^+(x)$ is the set of sets which contain x. Classical mathematics mostly deals with the case when G is a simplicial complex, meaning that G is closed under the operation of taking finite non-empty subsets. We will see that sometimes this assumption is important and that sometimes, it is not. If $G$ has n elements, one can look at the $n \times n$ matrix $L(x,y) = H(W^-(x) \cap W^-x(y))$ which is the energy of the hetero or homoclinic set obtained by intersecting stable manifolds. One can also look at $g(x,y) = H(W^+(x) \cap W^+(y)) \omega(x) \omega(y)$ . It is quite amazing that in general, not even requiring the only axiom in a simplicial complex, for an arbitrary set of sets, one has ${\rm det}(L)={\rm det}(g) = \prod_{x \in G} h(x)$ . Furthermore, if $h$ takes values in $U = \{ |z|=1 \}$ (this works in more general set-ups even like division algebras or $C^*$ algebras), that then $g = L^{-1}$ . This is pretty amazing as this implies for example that we have integer matrices which are inverse of each other. The number of negative energy values of $h$ is the number of negative eigenvalues of $L$ or $g$ . Especially, if $h(x)=1$ for all $x \in G$ , then $L,g$ are positive definite integer quadratic forms which then also are iso-spectral. This is a symplectic relation. This paragraph can explain a bit why I abandoned Wu characteristic for a while. The connection calculus was just a too exciting topic to not pursue more. I feel that nature wants to tell us something here because most technical problems we experience in classical mathematical set-ups are infinities. They manifest for example due to unbounded operators or infinite Green function diagonals. The Newton potential 1/r comes from the Green function of the standard Laplacian $-\Delta/(4\pi)$ in three-dimensional space $G=\mathbb{R}^3$ and this leads to infinities because if two electrons come together, the potential gets infinite. Similarily, the gravitational force becomes infinite but we never really worry about this. When computing the electric potential at a point, we conveniently neglect the potential of the electron itself; when computing the Zeta function of the Riemann zeta function (which is the spectral zeta function of the circle), we conveniently leave away the zero eigenvalue. It is a regularized determinant, a regularized zeta function. All such dancing around zero and infinities is absent in connection calculus because there is never a 0 eigenvalue. Of course, the classical Laplacians are important also in the discrete: the dimension of the Harmonic spaces, the kernels of the Laplacian on various form sectors produce cohomology. This allows to compute the cohomology of a simplicial complex in a handful of lines without invoking any external libraries. For the cohomologies of the Wu characteristic, which are more involved to compute because the incidence matrices are huge, also the code is about twice as long (a dozen lines). In principle, if we have a compact manifold, produce a triangulation which is locally contractible (it does not even have to be nice as it is independent of homotopies) and get a basis of the cohomology group using the Hodge theorem and the Hodge theorem is also the key to compute the cohomology for Wu characteristic.

Introduction

About connection calculus.

Author: oliverknill