Complex energized complexes - Quantum Calculus

Definitions

Let $G$ be a finite abstract simplicial complex with $n$ sets and $h:G \to \mathbb{C}$ a wave. It defines an energy $h(A) = \sum_{x \in A} h(x)$ for any subset $A$ of $G$ . Define the $n \times n$ connection matrix $L(x,y) = h(W^-(x) \cap W^-(y))$ . Define also $\omega(x) = (-1)^{{\rm dim}(x)}$ where ${\rm dim}(x) =|x|-1$ and $|x|$ is the cardinality of $x$ . Define $g(x,y)=\omega(x) \omega(y) h(W^+(x) \cap W^+(y))$ . The core $W^-(x)$ is the set of sets contained in $x$ and the star $W^+(x)$ is the set of sets containing $x$ . Let $\mathbb{U}$ denote the set of units in $\mathbb{C}$ which is the unit circle $U(1)$ .

[Update August 23: a paper [PDF] is available.]

Basic results

The following results hold for all division algebra $\mathbb{R}, \mathbb{C}, \mathbb{H}, \mathbb{O}$ and its units $\mathbb{U}$ which are $\mathbb{Z}_2$ , $U(1)$ , $SU(2)$ , or $\mathbb{S}^7$ . The reason is that both $L$ and $g$ do not tap into the multiplicative structure of the algebra. For the determinant, one has to take Study determinant rsp Dieudonne determinant, which in the case $\mathbb{C}$ is the absolute value of the usual determinant. The following results were already announced in the complex in our article [PDF].

Theorem 1 (Determinant formula) $det(L) = \prod_{x \in G} h(x)$ .

Theorem 2 (Energy theorem) $\sum_{x,y} g(x,y) = H(G)$ .

Theorem 3 (Green Star) If $h$ is $\mathbb{U}$ valued, then $g^* L = L g^*=1$ .

For the last formula one can even drop the finiteness assumption. The simplicial complex could be infinite like the Whitney complex of some infinite graph like $Z$ . For defining H(G) or $det(L)$ in the infinite case, one would have to refer to ergodic theory if there is some periodicity (a lattice for example) or almost periodicity (like often looked at in solid state physics where one looks at almost periodic operators for example) because $log(det(L))$ can be expressed as a limit of Birkhoff sums. Also the Energy theory would have to be normalized by doing averages.Both sides are then ergodic limits of finite sums. The only thing we really need beside some ergodic regularity when averaging over larger and larger regions is that there is an upper bound on size of the stable manifold. What would not work is a simplicial complex like a star graph with infinitely many spikes where one vertex has infinite vertex degree. Lattices, randomly generated networks (by some reasonable stochastic growth process which makes sure that there is some upper bound on the vertex degree) assures that the Green function entries remain bounded.

If you want to experiment,Here is the code [Mathematica TXT].

(* Connection Laplacian defined by a complex wave, Oliver Knill, 1/8/2020  *)
Generate[A_]:=Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1];
RandomSets[n_,m_]:=Module[{A={},X=Range[n],k},Do[k:=1+Random[Integer,n-1];
  A=Append[A,Union[RandomChoice[X,k]]],{m}];Sort[Generate[A]]];
G=RandomSets[5,9]; n=Length[G];
S=Table[-(-1)^Length[G[[k]]]*If[k ==l,1,0],{k,n},{l,n}]; (* Super matrix   *)
star[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[v,x],u=Append[u,v]],{k,n}];u];
core[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[x,v],u=Append[u,v]],{k,n}];u];
Wminus     = Table[Intersection[core[G[[k]]],core[G[[l]]]],{k,n},{l,n}];
Wplus      = Table[Intersection[star[G[[k]]],star[G[[l]]]],{k,n},{l,n}];
e=Table[Exp[2Pi I Random[]],{k,n}];
energy[A_]:=If[A=={},0,Sum[e[[Position[G,A[[k]]][[1,1]]]],{k,Length[A]}]];
Lminus     = Table[energy[Wminus[[k,l]]],    {k,n},{l,n}];  L  =      Lminus;
Lplus      = Table[energy[Wplus[[k,l]]],     {k,n},{l,n}];  g  =   S.Lplus.S;
Print[{
Chop[Total[Flatten[g]] - Total[e]],                    (* Energy Thm       *)
Chop[Tr[S.g] -Total[e]],                               (* McKean-Singer Thm*)
Chop[{Det[g],Det[L],N[Product[e[[k]],{k,n}]]}],        (* Unimodularity Thm*)
N[Total[Flatten[Conjugate[g].L -IdentityMatrix[n]]]]}];(* Green-Star Id    *)

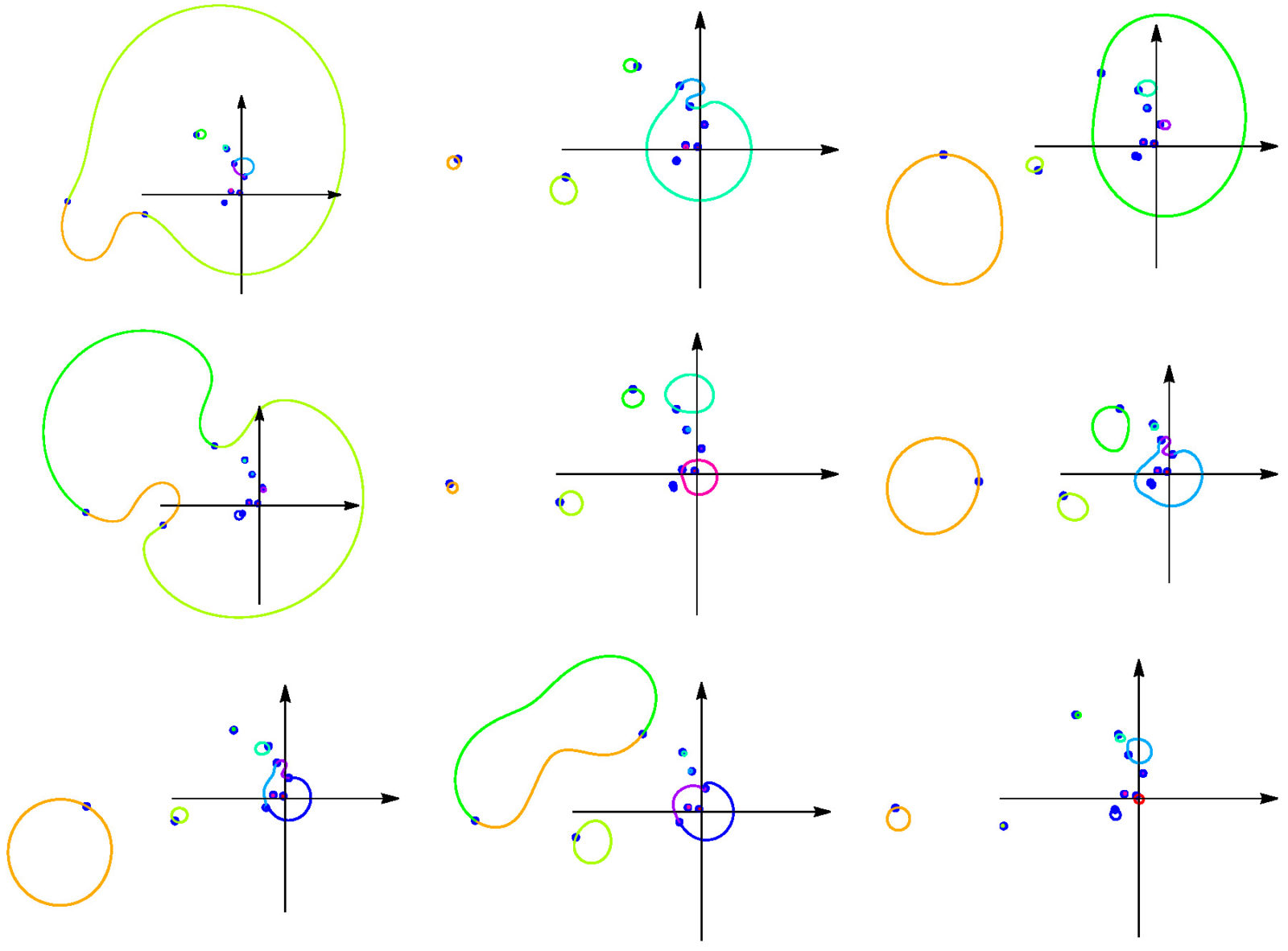
New phase phenomenon

In the real case we have seen that the number of negative eigenvalues of $L$ is equal to the number of negative $h$ values. There is no obvious analogue in the complex. However, we can look what happens if we deform the wave $h(x) \to e^{i \theta} h(x)$ at some simplex. This produces a deformation of the spectrum $\sigma(L(\theta))$ . Obviously because at $\theta=0$ and $\theta=2\pi$ we have the same matrix. It was totally unexpected however to track the eigenvalues and see the circle deformation of the wave when $\theta$ ranges on a circle from $0$ to $2\pi$ does actually permute the spectrum in a nontrivial way. For all $h$ for which $L(G,h)$ has simple spectrum, we can define a permutation group $P(G,h)$ generated by all these basic deformations.

Theorem The group $P(G,h)$ is non-trivial and non-Abelian in general.

Since the group is constant on any connected open set of $h$ values, it follows that the set of waves $h$ for which the spectrum of $L(G,h)$ is simple is in general not connected. Furthermore, there are cases, where some connected component in this manifold contains a nonlinear permutation group $P(G,h)$ in the fundamental group. This rises a lot of questions about the nature and topology of the manifold of all these matrices $L(G,h)$ . Even the disconnectedness is a surprise as we can connect two points if we do not care about collisions of eigenvalues.We would have expected that it is possible to avoid connections as they are lower dimensional parts in a complex manifold.

We see the Spectral curves for a simplicial complex with 9 sets. This shows how the eigenvalues move in the complex plane if one changes the wave phase at some simplex. We see that sometimes, we need to turn the gauge wheel more than 360 degrees to get back to the original eigenvalue. In the case when turning the fourth wheel, we need to turn by 1080 degrees to get back. We rotate three of the eigenvalues cyclically. All these deformations produce permutations which then generate a group of permutations of the spectrum. This group is stable under deformation of h as long as we have simple spectrum. It follows that in this case, there are more than one connected components in the manifold matrices L(x) for which the spectrum is simple. We would have expected this to be a connected set.

Questions

There are many questions now: some might be difficult and I’m still making experiments.

Which spectra can be obtained? Given n complex numbers different from zero. Are the complex numbers $h(x)$ for the n simplices such that the spectrum of L(x) is that given set?
Related: Is it possible in particular to hear wave $h$ from the spectrum $\sigma(L(G,h))$ ?
What happens in the non-commutative division algebra cases, where the units are simply connected spaces and where there is some subtleties with the eigenvalues?(there is no fundamental theorem of algebra of the same kind as there are equations like $x^2+1=0$ which have many solutions).
What kind of permutation groups are possible? What kind of permutation groups can appear simultaneously for the same simplicial complex? Does this have anything relation with the topology of G.
What happens with these permutation groups in the Barycentric limit $G_n$ with $n \to \infty$ . The Barycentric limit is interesting. While the vertex degrees explodes there of course, we still have a chance that with the right energy h distribution, we have an invertible limit.
Is there always a solution of the fixed point equation $\sigma(L(G,h)) = h(G)$ ? It appears to be the case in the real case.

The eigenvalues are some sort of energies in a quantum mechanical ssense and the wave values $h(x)$ too assign some initial energy to a simplex. In some sense, we have a quantum field theory because a quantum wave h defines an operator L(h) which then has eigenvalues and eigenvectors. It is all related with energy because $g(x,y)$ , is a potential theoretical energy between the simplices $x,y$ (that analogy comes from the fact that if L is the usual Laplacian in three dimensional space, then g(x,y)=1/|x-y| is the potential used in gravitational or electromagnetic frame works. The motivation is of course to have a natural wave $h=h(G)$ (defined by a fixed point equation) for every simplicial complex and that in the Barycentric limit, there is no input any more at all, except the dimension. Maybe also that in the Barycentric limit, we get some phenomena which are physically relevant like the value of the lowest energy.

Definitions

Basic results

New phase phenomenon

Questions

Author: oliverknill