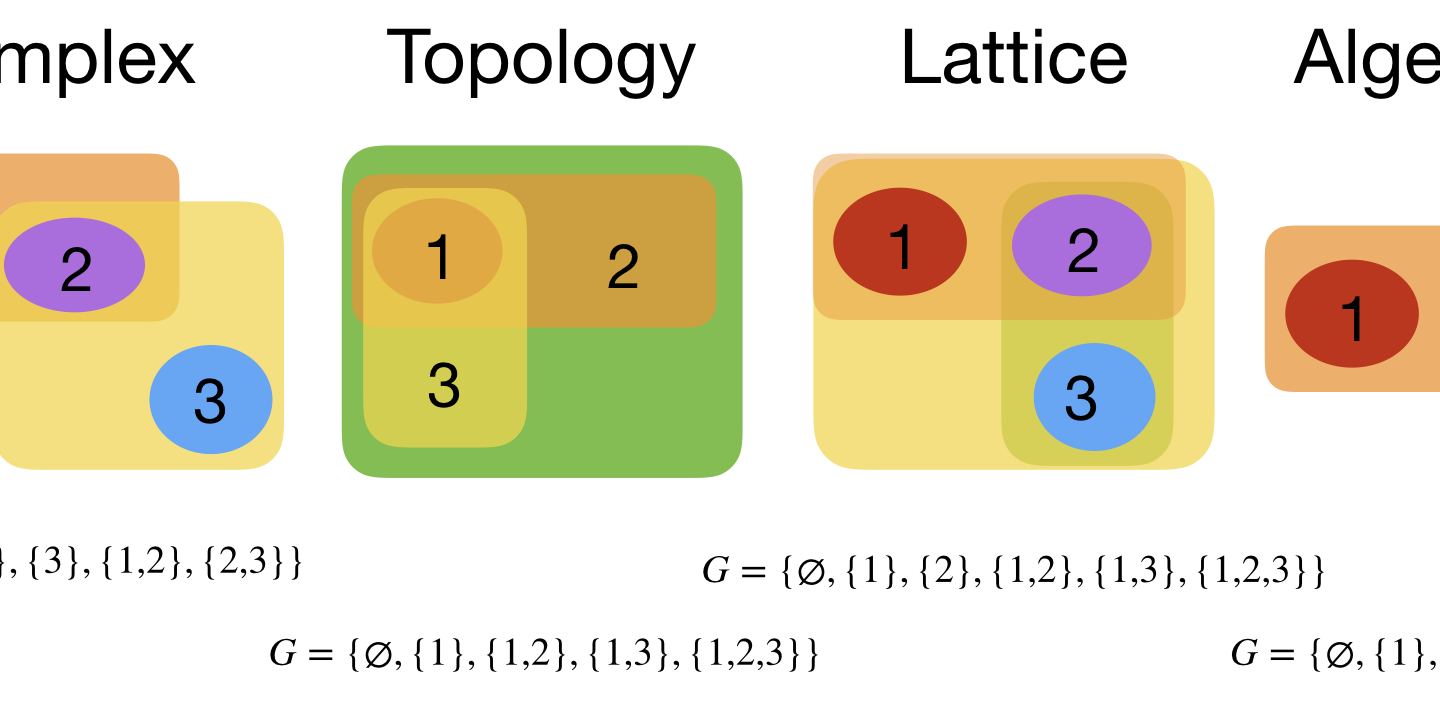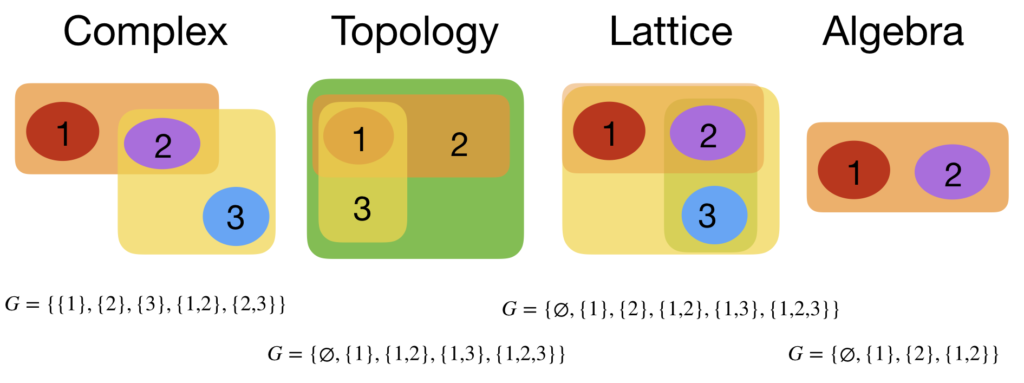
The joy of sets of sets - Quantum Calculus

The simplest construct in mathematics is probably a finite set of sets. Unlike a simple set alone, it has natural algebraic, geometric, analytic and order structures built in. In the finite case, there is lot of overlap but still, there is a rich variety of structure.

Algebraic structure

An example of a an algebraic structure is to have the symmetric difference as addition and the intersection as multiplication. If the set of sets is invariant under both operations and contains the empty set and the union of all sets, then we have a commutative ring with 1. The empty set is the zero element, the union of all sets it the 1-element. It is a Boolean algebra with the property A+A=0 and A*A=A. Arithmetic can come in in various ways. What was just mentioned is the situation when the elements of G are the elements of an algebraic object and the operation is an operation on G. One can also look at operations on geometries G and the disjoint union is one of them which makes the elements of the category into a monoid.

Analytic structure

An example of an analytic structure is a $\sigma$ -algebra, it is used in probability theory, where one has additionally a probability measure defined. On finite probability spaces, such a probability measure is defined by assigning to every set $\{j\}$ with one element has some probability $p_j$ . The association with analysis comes because functional analytic objects like function spaces are defined in the form of random variables. In mathematics, it is a bit difficult to define what “analysis” is, as it consists of so many different fields: real analysis, complex analysis, functional analysis, harmonic analysis, calculus of variations, spectral theory, stochastic calculus or partial differential equations are all huge fields and usually considered part of analysis. What is an ingredient in all is that there is some sort of calculus involved with computing rate of changes (marginal quantities) or integration (expectation). In the case of finite sets, all of this can be done much easier (of course most of the time missing some important part of the continuum model). For example, one can look at PDE’s on graphs and this applies also for finite set of sets as any finite set of sets defines graphs, one of them being the Barycentric refinement in which two sets are connected if one is contained in the other.

Order structure

An example of an order structure is a lattice, where we have invariance under union and intersection. An important order structure is a poset, a partially ordered set. Every finite set of sets automatically comes with a partial order structure as we can define $x<y$ if $x \subset y$ . The subset relation is reflexive, anti-symmetric and transitive. The nice thing (the joy!) of finite sets of sets is that one does not have to impose the Poset axiom system but has it for free. The three axioms are built in the notion of subset. The notion of poset so to speak is more general then, however for finite posets, one can always realize them as finite sets of sets. In order to see that posets are important one can refer to statements of masters in the subject. In this essay is put as one of the big ideas in combinatorics.

Topological structure

In topology one looks at topologies or simplicial complexes. Finite topological spaces define notions like continuity, connectivity or various separation properties like the Hausdorff property. Simplicial complexes are more used in algebraic topological set-ups. When thinking about topology as well as also about simplicial complexes, one often has a continuum picture in mind. Topology is “rubber band geometry” for example. Simplices are often (rather old-fashioned however) thought of as realized as simplices in n-dimensional space. The continuum is actually not needed. In the discrete and especially in a finite set-up, one does not want to use the axiom of infinity even. A finite topological space or a finite abstract simplicial complex has no need to be realized in the continuum. For a finitist, it would not even matter, if somebody would prove ZFC is not consistent.

Arithmetic structure

One can look at sets of sets as “numbers”, elements with which one can do arithmetic. The addition is the disjoint union, the multiplication is the Cartesian product. There are relations with dual constructs which include the join operation known in topology. https://www.youtube.com/watch?v=FZGIrLiVeOc explains it a bit: if there are n sets in G, define a $n \times n$ matrix $L$ which has as entries $L(x,y)$ the number of sets which are both in $x$ and $y$ . A dual matrix to that is $L(x,y)$ which counts the number of sets which contain both $x$ and $y$ . In order to see this from a representation point of view, one has to add an algebraic structure on the category of finite sets of sets. Taking the disjoint union gives a monoid structure which by general principles (Grothendieck completion) extends to an Abelian group. But there is even a ring structure as we can take the Cartesian product as multiplication. Now, the matrix L(G) associated to a finite set of sets G behaves nicely. When adding two structures G+H, then the matrices are added as a direct sum $L(G) \oplus L(H)$ . When taking the Cartesian product, we get the tensor product of $L(G) \otimes L(H)$ of the corresponding matrices.

Representation theoretic structure

If one assigns to a set of sets a matrix, one is in the realm of representation theory, especially if this assignment shows compatibility with the structure. The connection matrix for example is nice in this respect and lead to a representation in a tensor algebra. It is a bit surprising that interesting matrices already appear when looking at a finite set of sets without any further assumption on the sets. This tensor representation is a representation in a larger sense in that the geometries G, the elements of the group are represented by matrices in a tensor ring. It is not that G+H becomes the matrix product.

Algebraic geometric structure

With a bit of more structure, one can get to other topics. An integer-valued functions on a finite set of sets can be seen as a divisor. The simplicial complex defines graphs in various ways, their Kirchhoff Laplacian L allows to define principal divisors (elements in the image of L, motivated by the continuum fact that $\Delta \log(f)$ is classically a divisor), effective divisors (nonnegative), linear systems (divisors equivalent to effective divisors modulo principal divisors), divisor class group $ker(\chi)/im(L)$ . So there is a bit of a playground with notions used in algebraic geometry. I did myself quite a bit of work in this in 2012 when learning the Baker-Norine theory. It is a fascinating story relating in the discrete with many other combinatorial topics.

Differential geometric structure

Also differential geometric notions come in. One can define a discrete Euler curvature for example and get Gauss-Bonnet, PoincarÃ©-Hopf, Morse theoretical notions are quite easy to implement, geodesic notions like exponential maps etc turn out to be tougher. It is actually quite an interesting theme for example to look at notions of curvature and especially sectional curvature. I myself started to work in this entire field by looking at notions of curvature. Here are some slides from 2014. At that time I still considered a graph to have positive curvature if all embedded wheel graph have less than 6 spikes. This is a very primitive notion modeling the notion of positive (sectional) curvature in the continuum. One can dismiss this this as too strong of a condition (it is!) but it is one where one can prove things. One has a sphere theorem for example in that every d-graph which has positive curvature in that sense is a d-sphere but the restrictions are clear in higher dimensions. If one defines negative curvature as a graph for which all embedded wheel graphs have 7 or more spikes, then in dimension 2, one can easily see that for every genus there are only finitely many species and that in dimension 3 or higher there are none (simply because unit spheres are spheres which must have some positive curvature somewhere). So, the notion of sectional curvature needs to be relaxed in order to get closer to the continuum. The problem is a bit like in physics: there are too many possibilities to generalize this (smoothing out curvature for example or looking at larger sets of two dimensional geodesic surfaces) but more importantly that for weaker notions, even weaker theorems like Synges theorem become more difficult to prove. Not to speak about sphere theorems.

Algebraic topological structure

The algebraic topological set-up in the finite case is probably even older than the continuum version. Kirchhoff pioneered discrete calculus notions before Betti and Poincare set things up, often with discrete simplicial complexes in the form of graphs. Graphs have historically been used early to describe higher dimensional phenomena. Even the start of graph theory, the KÃ¶nigsberg bridge problem deals with a two dimensional topological problem. What happened is that especially the literature on graph theory looked at graphs as one-dimensional simplicial complexes having only zero and one dimensional cohomology for example. Whitney for example, who wrote his thesis in graph theory saw it differently and also developed the first really sane notion of “manifold”. The clique complex is a structure imposed on a graph which serves like a topology or sheave or sigma algebra as an additional structure. Algebraic topology can be done very intuitively on graphs. And it can also be taught in freshmen calculus.

Physics

Finally, one can ask, whether finite sets of sets are relevant in physics. Mathematically a lot of things are directly mirrored. Once, one has an exterior derivative, one has notions like div, curl, grad in any dimension, has a Laplacian. Classical field theories do not need even a change of language: one can do electromagnetism F=dA, LA=j and so dF=0,d*F=j (with the Laplacian on 1 forms like the electromagnetic potential A or the current j), gravity L V=s (Gauss form with the Laplacian on 0-forms giving the potential V from the mass density s), look at dynamical systems, like wave or SchrÃ¶dinger equations, one can study spectra and their relation to the geometry etc. (Maybe look at this handout). There are things where one has to deviate more, like in relativity, where notions of curvature like Ricci curvature can look very different in combinatorics, different in the sense what theorems one can prove. A start is to study variational problems like extremizing functionals like the Euler characteristic on classes of finite geometries. But physics is a bit different from mathematics in the sense that one has to build models which explain measured data. A valuable theory must explain at least one phenomenon without any competing theory doing it better. Otherwise, it will end up in the garbage bin or remain in a mathematical theory (and is only physics in an extended sense that it can be realized in some mathematicians brain). So far, finite geometries miserably fail to describe the motion of a planet, or the structure of the hydrogen atom or what happens with a black hole if it evaporates away.