The connection matrix of a simplicial complex G with n elements was the matrix L(x,y)=1 if x and y intersect and L(x,y)=0 if they do not. This matrix was unimodular. The set-up can be generalized vastly. Given any function h on G one can look at L(x,y) to be the energy of the intersection of x and y which is the sum over all h(z), where z is a set both in x and y. For unimodularity, we do not need even the simplicial complex structure any more. If h takes values in {-1,1}, then the matrix L is still unimodular. We have seen already the case where h is constant 1. In that case, the matrix L is a positive definite quadratic form which has the property that the eigenvalues of L are the eigenvalues of the inverse.
For a preprint, see http://www.math.harvard.edu/~knill/graphgeometry/papers/energized.pdf .
If $G$ is a set of sets and $h:G \to \mathbb{R}$ is a function, we can assign an energy $E[A]$ to a subset of $G$. For two points $x,y \in G$, let $W^{–}(x,y)=W^-(x) \cap W^+(x)$ be the set of sets contained both in $x$ and $y$ and $W^{++}(x,y)=W^+(x) \cap W^+(y)$ the set of sets containing both $x$ and $y$. This defines the integer matrices $L^{–}(x,y) = E[W^{- -}(x,y)]$ and $L^{++}(x,y) = E[W^{++}(x,y)$.
Generalized Unimodularity theorem: $\det(L^{++}) = \det(L^{- -}) = \prod_x h(x)$. The number of positive eigenvalues of $L^{++}$ or $L^{- -}$ is the same than the number of positive entries for $h$.
In the case $h(x) \in { -1,1 }$ this implies unimodularity. With the super matrix $S(x,y) = \delta(x,y) (-1)^{{\rm dim}(x)}$, we define $L=L^{–}$ and $g=S L^{++} S$. Now $L g=1$. In the case $h(x)=(-1)^{{\rm dim}(x)}$ we have $E[G]=\chi(G)$, the Euler characteristic and $\chi(G)$ is the number of positive eigenvalues minus the number of negative eigenvalues of $L$.
In the case $h(x) = 1$, the two matrices $L^{++},L^{- -}$ are isospectral positive definite matrices and have the spectral property $\sigma(L)=1/\sigma(L)$. The matrices $L^{++},L^{–}$ define unimodular integral quadratic forms and so dual integral lattices.
In that case, a consequence is:
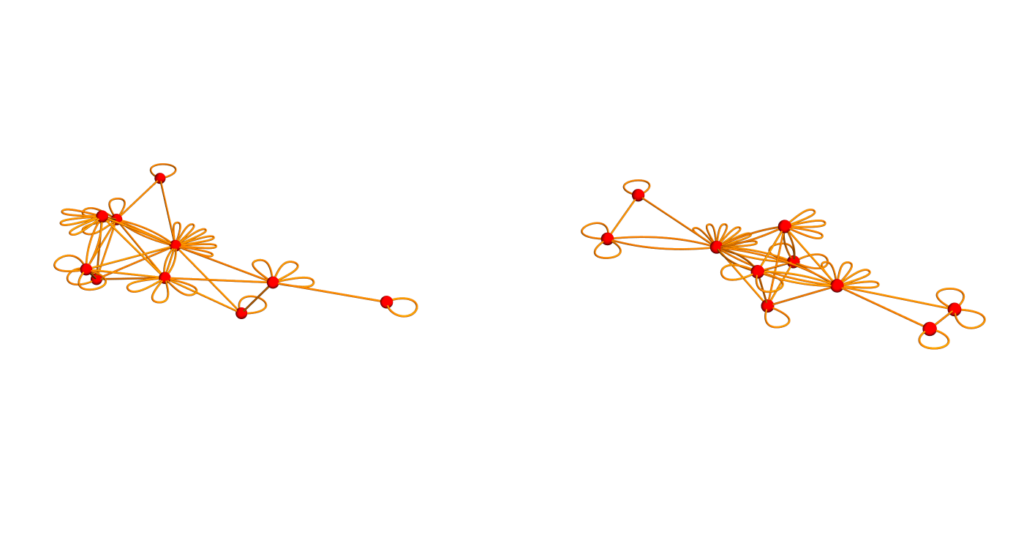
Isospectral Multigraphs: The multi-graphs $\Gamma^{++}, \Gamma^{–}$ defined by having $L^{++},L^{- -}$ as adjacency matrices.
R[n_,m_]:=Module[{A={},X=Range[n],k},Do[k:=1+Random[Integer,n-1];
A=Append[A,Union[RandomChoice[X,k]]],{m}];Sort[Union[A]]];
G=R[6,10];n=Length[G];e=Table[1,{n}];
energy[A_]:=If[A=={},0,Sum[e[[Position[G,A[[k]]][[1,1]]]],{k,Length[A]}]];
star[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[v,x],u=Append[u,v]],{k,n}];u];
core[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[x,v],u=Append[u,v]],{k,n}];u];
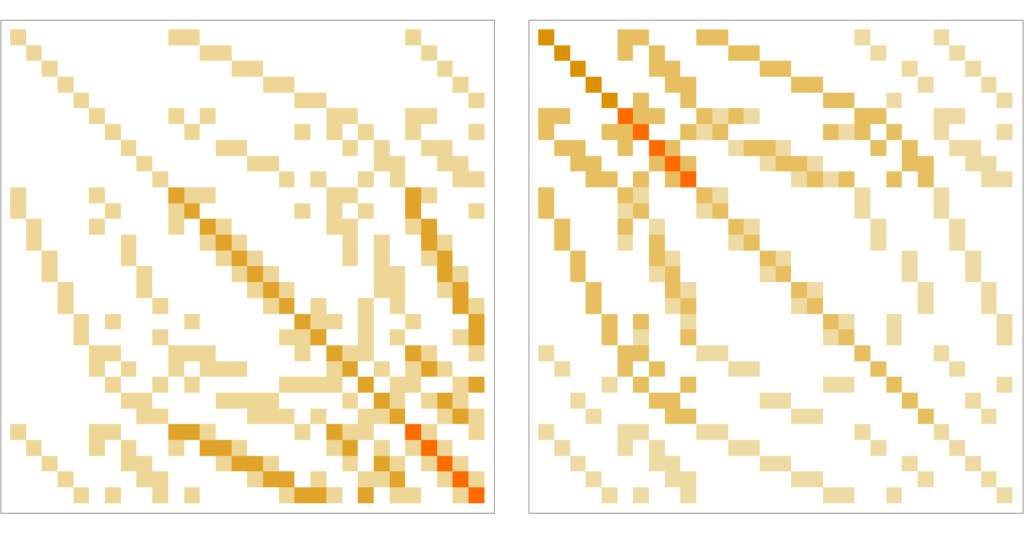
Wminus=Table[Intersection[core[G[[k]]],core[G[[l]]]],{k,n},{l,n}];
Wplus=Table[Intersection[star[G[[k]]],star[G[[l]]]],{k,n},{l,n}];
Lminus=Table[energy[Wminus[[k,l]]],{k,n},{l,n}];
Lplus=Table[energy[Wplus[[k,l]]],{k,n},{l,n}];
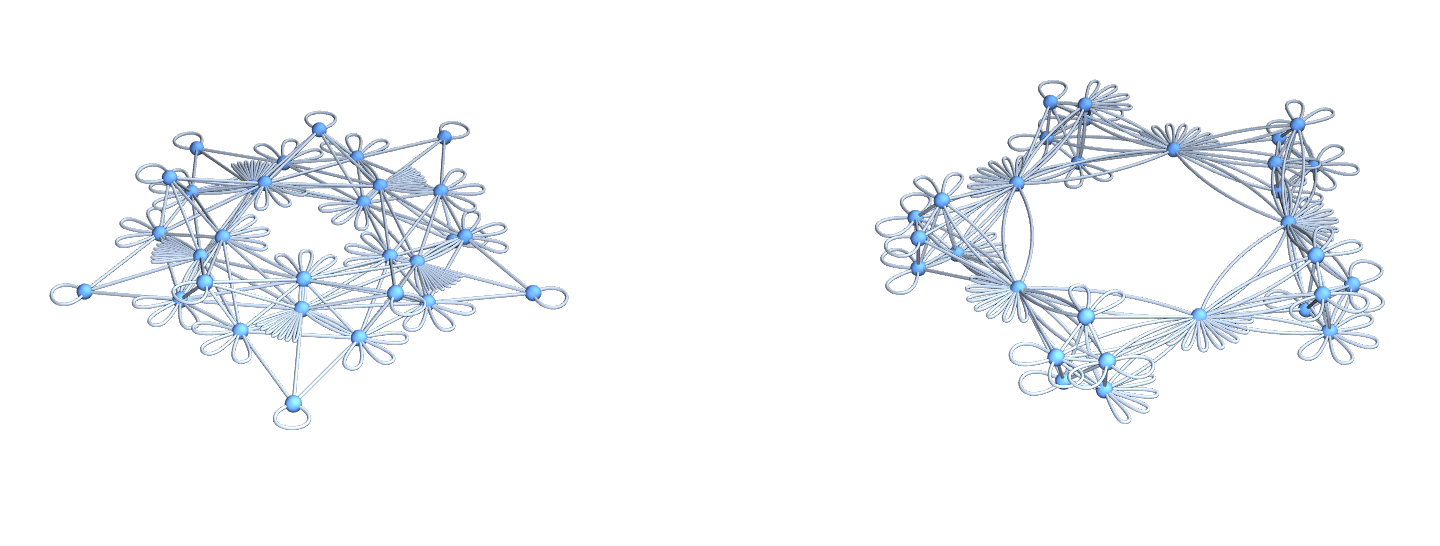
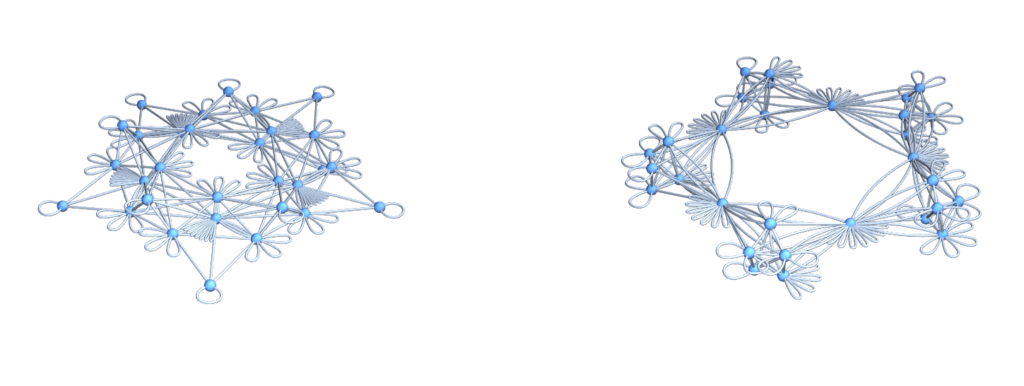
U=Graph[Flatten[Table[Table[G[[k]]<->G[[l]],{Lminus[[k,l]]}],{k,n},{l,k,n}]]];
V=Graph[Flatten[Table[Table[G[[k]]<->G[[l]],{Lplus[[k,l]]}],{k,n},{l,k,n}]]];
DrawGraph[s_]:=GraphPlot3D[s,VertexStyle->Red,EdgeStyle->Orange];
Print["Isospectral:",Eigenvalues[Lminus]==Eigenvalues[Lplus]];
GraphicsRow[{DrawGraph[U],DrawGraph[V]},ImageSize->700]
Here are some slide. Note that for the result that the inverse of L is conjugated to L, this requires the set G of sets to be a simplicial complex and not just a set of sets. The isospectral graph construct only needs a set of sets.