The video below is an attempt to get back to an older story of Wu characteristic. One of the things which still needs to be explored badly is the Wu cohomology of the complement K of knots H and more generally of the complement K of k-dimensional manifolds H in d-manifolds G. The new Sard approach allows now to do this more effectively as the surfaces in a host manifold are by definition already open sets and the complement closed. In order to get invariants which correspond to invariants in the continuum we need is to make sure that the complement K of H in G is a manifold with boundary. This might need some refinement first, but not a Barycentric refinement of G which is too heavy. We can just refine near the submanifold H. We need to work on this still so that we can experiment and see whether the Wu invariants are of any good for example for knots.
The story of Euler characteristic is also the story of simplicial cohomology. Many theorems are related to this. This math table talk from 8 years go March 8th 2016(PDF) summarizes this. Some of the most amazing theorems in mathematics: Gauss-Bonnet, Poincare-Hopf, Euler-Poincare,McKean-Singer, Steiniz-DeRham, Brouwer-Lefschetz, Riemann-Hurwitz or Riemann-Roch tell the story of Euler characeteristic. This generalizes vastly as maybe best illustrated by Atiyah-Singer or Atiyah-Bott (see this blog entry about the discrete, written down here). The generalization is that instead of replacing the elliptic complex coming with the Laplacian with a more general elliptic complex. In a first part, the combinatorial description of an invariant is reformulated with cohomology. This is possible if one has a McKean-Singer symmetry as one can then just look at the super trace of the heat kernel. At time t=0, one has the combinatorial version, at t=infinity one has the cohomological description as the heat flow at t=infinity is the projection onto Harmonic forms aka cohomology. This works also in the dynamical Lefschetz case. All these things are rather awkward in the continuum as it is riddled with technicalities which are important of course but not actually interesting. In the discrete, all complications are done. We do not have to work to show that there is a discrete set of eigenvalues of a differential operator or to make sure that the fixed point set of a map is “nice” like consisting of finitely many points. In the discrete we simply don’t care as the result always works. The Lefschetz fixed point formula for the identity map (where every point is a fixed point) is just the Euler-Poincare formula. We also do not need crazy sheaf theoretical constructs. We can just look at functions simplices. Functions on k-simplices are k-forms. No need for Clifford type constructions to define the Dirac operator. The Hodge Laplacian by definition already is the square of an other matrix. All this works whenever we have a Dirac matrix. It especially works if we have a Delta set and especially for simplicial sets. The Dirac matrix encodes there the face maps. Since for Delta sets, the Hodge blocks can be empty matrices. We therefore have to attach to each block a dimension to have all information of the delta set.
Having “trivialized” classical results, one can move on to other stories. One possibility is to deform the Dirac matrix in an isospectral way. It does not change the cohomology although and is just the same story but in an other coordinate system. But it is interesting because only the Dirac matrix gets deformed, not the Laplacian. Since by Connes, the Dirac matrix gives us distances the deformation changes distances and produces an inflationary start. This is featured in this blog entry with detailed code. But still, also this story can be done in the continuum. Its just that instead of ordinary differential equations which due to integrability have global solutions, we need in the continuum to deal with pseudo differential operators and would have to set up a nice function space in which the Lax type differential equation D’=[B(D),D] makes sense. I fought a bit about such matters when looking at Toda deformations of random operators in my thesis. For integrable systems, the isospectral matter makes it impossible to have blow up of solutions.
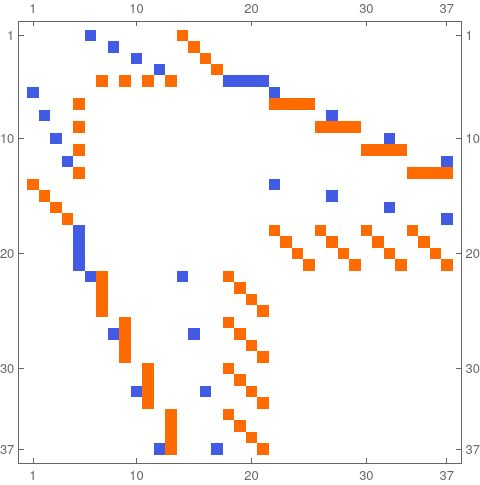
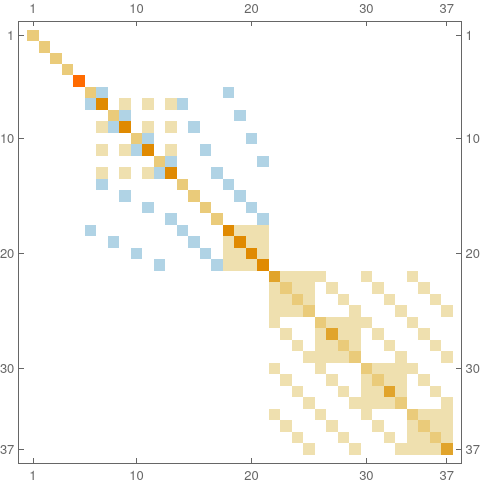
Wu characteristic is a new, completely different beast. And so far, there seems to be nothing which comes close in the continuum. In the discrete we can look at a different cochain complex, in which we look at functions of pairs of implices which intersect. The k dimensional pieces are now pairs of intersecting simplices whose dimensions add up to k. What happens now is that cohomology is no more a homotopy invariant but a topological invariant. For example, for a 2-simplex (triangle), the simplicial Betti vector is (1,0,0). The Wu Betti vector is (0,0,1,0,0). For the 3-simplex the Betti vector is (1,0,0,0) and the Wu Betti vector is (0,0,0,1,0,0,0). For a manifold G with boundary dG, the Wu characteristic is X(G)-X(dG). In some sense, the Wu characteristic of a manifold with boundary is the Euler characteristic of the interior of G. As for an other example, Let G be the star complex {{1}, {2}, {3}, {4}, {5}, {1, 2}, {1, 3}, {1, 4}, {1, 5}}. It has Betti vector (1,0), Euler characteristic 1. The Wu Betti vector is (0,0,5) and the Wu characteristic is 5. There are 37 simplex pairs. The Dirac matrix is a 37 x 37 matrix (to the left), the Laplacian 
