For a finite abstract simplicial complex $G$ with $n$ sets we can look at the $n \times n$ matrix K(x,y) which counts the number of simplices in the intersection of x and y. We have seen already that the 0-1-connection matrix $L$ which is $L(x,y)=1$ if $x$ and $y$ intersect and $0$ else has determinant 1 or -1. Also $K$ is unimodular. But this is an understatement: $K$ always has determinant 1. It is an element of $SL(n,Z)$. The inverse of $K$ is explicitly given as $K^{-1}(x,y)=\omega(x) \omega(y) |St(x) \cap St(y)|$, where $St(x)$ is the star of $x$, the sets in $G$ which contain $x$. The matrix $K$ is positive definite. The spectrum of $K$ and $K^{-1}$ agree so that its Hydrogen matrix or super charge $Q=K-K^{-1}$ has spectrum $\sigma(Q)=-\sigma(Q)$. This implies that the zeta function $\zeta(s) = \sum_{k=1}^n \lambda_k^{-s}$ is symmetric with respect to the imaginary axes. The sum $\sum_{x,y} K^{-1}(x,y)=n$ is the number sets in $G$.
Theorem: K has determinant 1, positive eigenvalues. If $\lambda$ is an eigenvalue, then $1/\lambda$ is an eigenvalue. The sum of the matrix elements $K^{-1}(x,y)$ is the number of elements in G.
See this write up [PDF] for more details and the time stamped ArXiv version for which one can always access the LaTeX source.
For the unimodularity of the connection matrix , $L$, see this write-up. In the wake of parametrized versions of Gauss-Bonnet and parametrized Poincare Hopf, and knowing the Green function entries g(x,y) explicitly, it is quite obvious how to generalize the energy theorem. There is a parametrized connection matrix $L_t$ and an inverse $g_t$ such that the sum of the Green function matrix entries $g_t(x,y)$ is $1-f_g(t)$, where $f_G(t)$ is the f-function of $G$. Now, the matrix $L_t$ has determinant $1$ if and only if $t=-1$ (which is the case already covered), or then $t=1$, which is a new case. There are only two unimodular cases. The case of L (Fermionic case) and the case of K (Bosonic case).
The matrices are exciting also from a physical point of view. Any Laplacian produces physics. But similarly as the connection Laplacian L already, the operator K is causal. Given two points, there is a local causal diamond (in GR discussed for example here) if we look at a space time. Classical potential theory of course is completely incompatible with principles of relativity. We need a short range potential to have a reasonable relativistic potential theory. Forces are exchanged with particles which travel with finite speed.
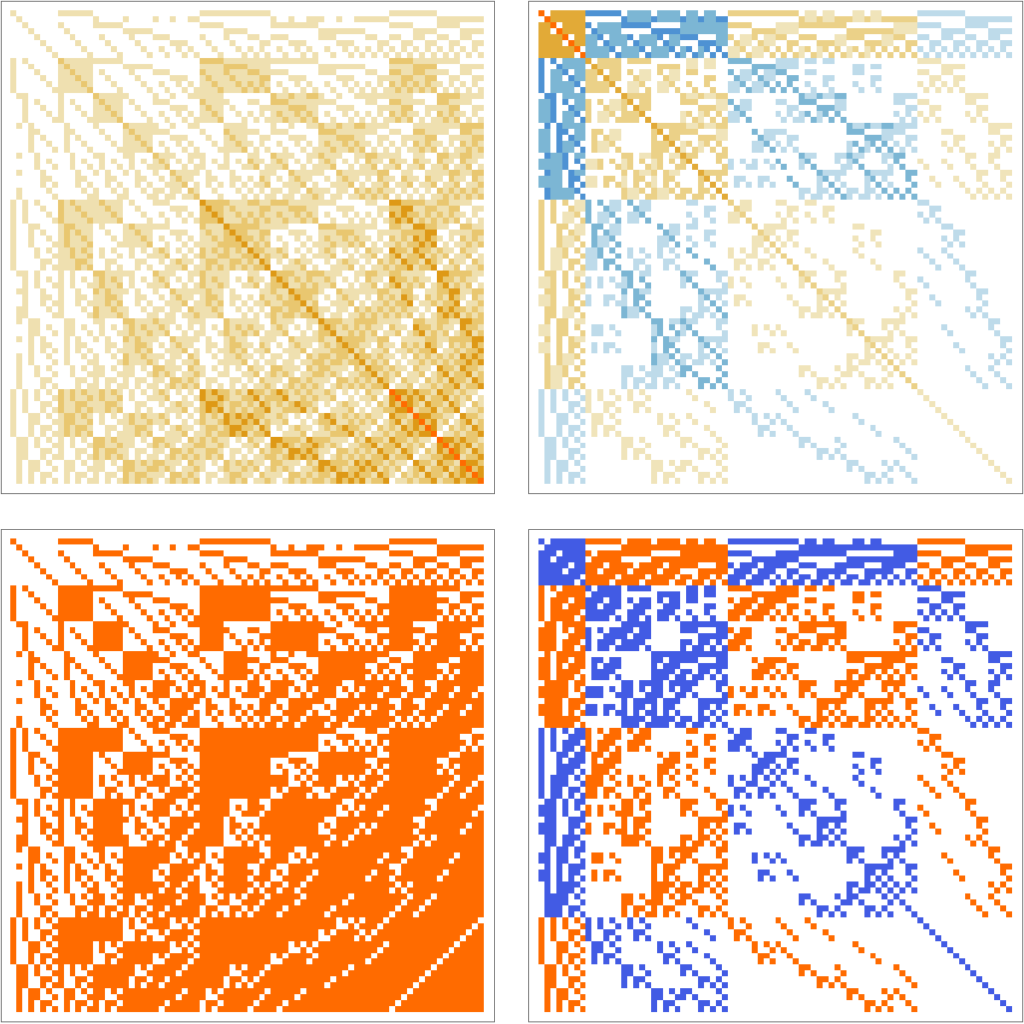
In the above illustration picture, we see first the counting matrix K and its inverse. Below we see the old connection matrix L (which is a 0-1 matrix) and its inverse. The matrix $K$ is richer as it contains more information than the matrix $L$. It is actually very easy to reconstruct the complex G from K which this is harder to do from L. The matrix L of course still interesting, as it is related more with topology: the total energy is the Euler characteristic which stays invariant under Barycentric refinements. When looking at the energy of K, it is natural take the uniform probability measure $\mu$ on $G$ and see $V(x)=\sum_{y} K(x,y) \mu(y)$ as a potential whoe total energy $\sum_x V(x) \mu(x)$ is equal to $1$.
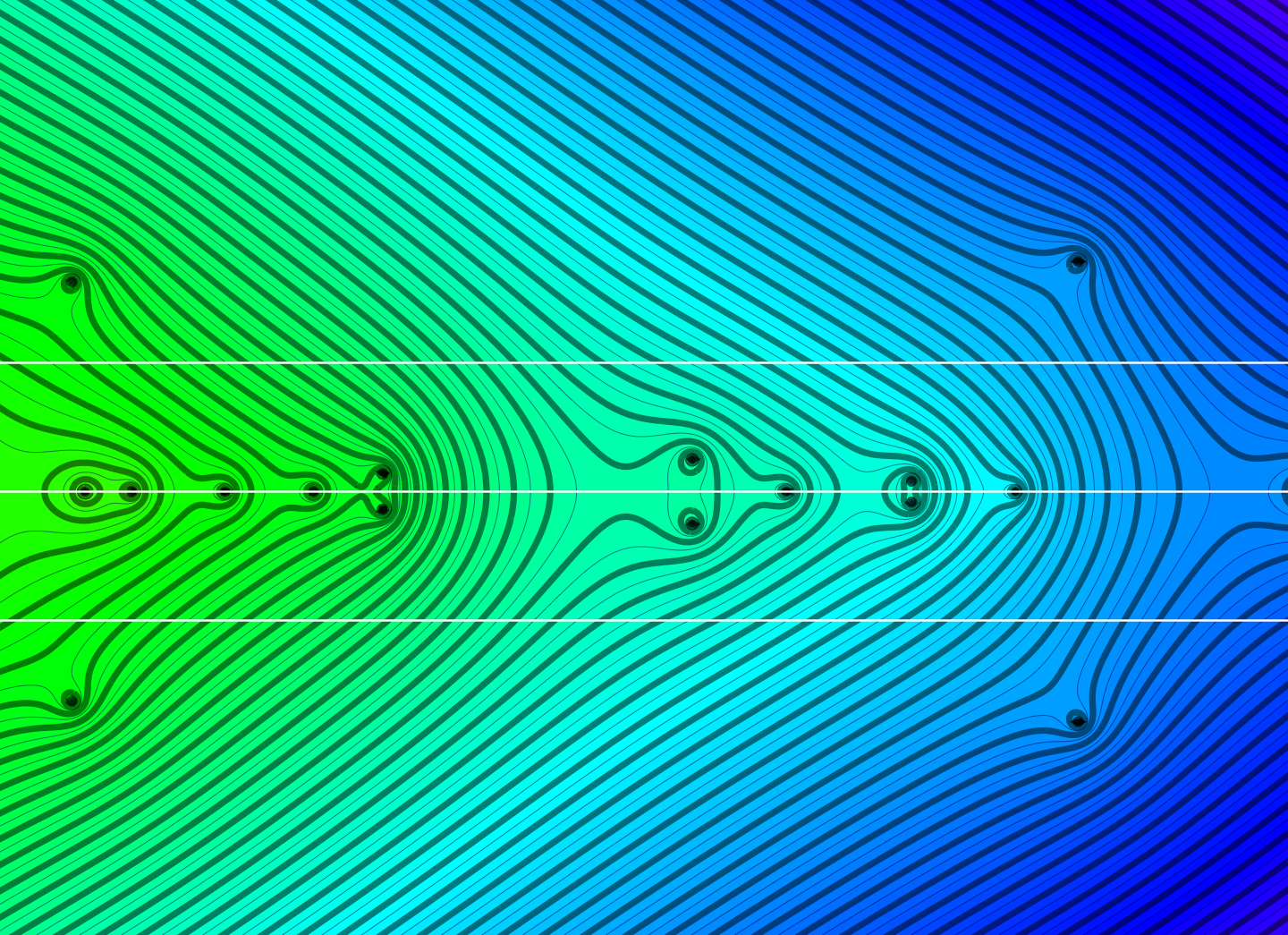
The picture to the right shows counting matrix zeta function of the 3-sphere simplicial complex. For all simplicial complexes, the function is symmetric with respect to the imaginary axes. This symmetry was present for the original operator $L=L_{-1}$ only in the one-dimensional case. For the zeta function $\zeta(s) = \sum_j \lambda_j^{-s}$, where $\lambda_k$ are the eigenvalues of $K$, this means that there is a functional equation. Now this is really exciting, as in the case t=-1, this was only possible in the one-dimensional case. See the Hydrogen identity paper.
What we do have now is that $D=K – K^{-1}$ has a symmetric spectrum and can serve as a what a physisist would call a super charge or Dirac operator to the Laplacian $H=D^2 = K^2 + K^{-2} -2$. Mathematically, iterating $K$ has a random walk interpretation and applying $K^{-1}$ is a random walk going backwards. There is some reversibility even so there is an arrow of time. The properties of K and $K^{-1}$ are not the same. In any case, we can look at the wave equation $u_{tt} = -H u$ and explicitly solve it as the wave equation with H becomes a Schroedinger equation for Q. As usual $u(t) = \cos(Q t) u(0) + \sin(Q t) Q^{-1} u'(0)$ but as $Q$ can have a kernel, the $Q^{-1}$ is a pseudo inverse. One does not have to worry if the initial velocity is chosen perpendicular to the kernel of $Q$.
Here is the rather poetic Mathematica code added to the paper:
Generate[A_]:=Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1];
R[n_,m_]:=Module[{A={},X=Range[n],k},Do[k:=1+Random[Integer,n-1];
A=Append[A,Union[RandomChoice[X,k]]],{m}];Generate[A]];
G=R[6,9];n=Length[G]; G=Sort[G]; w[x_]:=-(-1)^Length[x];
star[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[v,x],u=Append[u,v]],{k,n}];u];
core[x_]:=Module[{u={}},Do[v=G[[k]];If[SubsetQ[x,v],u=Append[u,v]],{k,n}];u];
Wminus=Table[Intersection[core[G[[k]]],core[G[[l]]]],{k,n},{l,n}];
Wplus =Table[Intersection[star[G[[k]]],star[G[[l]]]],{k,n},{l,n}];
K = Table[ Length[Wminus[[k,l]]],{k,n},{l,n}];
KI= Table[w[G[[k]]]*w[G[[l]]]*Length[Wplus[[k,l]]] ,{k,n},{l,n}];
EV = Sort[Eigenvalues[1.0*K]]; Clear[s]; ZetaFunction=Total[EV^(-s)];
CharPol=CoefficientList[CharacteristicPolynomial[K,s],s];
Print["Green Star formula: ",Simplify[K.KI==IdentityMatrix[n]]];
Print["Energy Theorem: ",Total[Flatten[KI]]==Length[G]];
Print["Spectral Symmetry: ",CharPol==(-1)^n*Reverse[CharPol]];