Zeta functions for Simplicial Complexes
For a finite abstract simplicial complex, we can look at the Dirac Zeta function, the Connection Zeta function and the Lefschetz zeta function. My work on this in the last couple of years
Category: zeta functions
Bounds on Graph Spectra
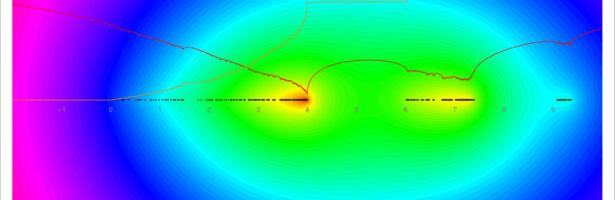
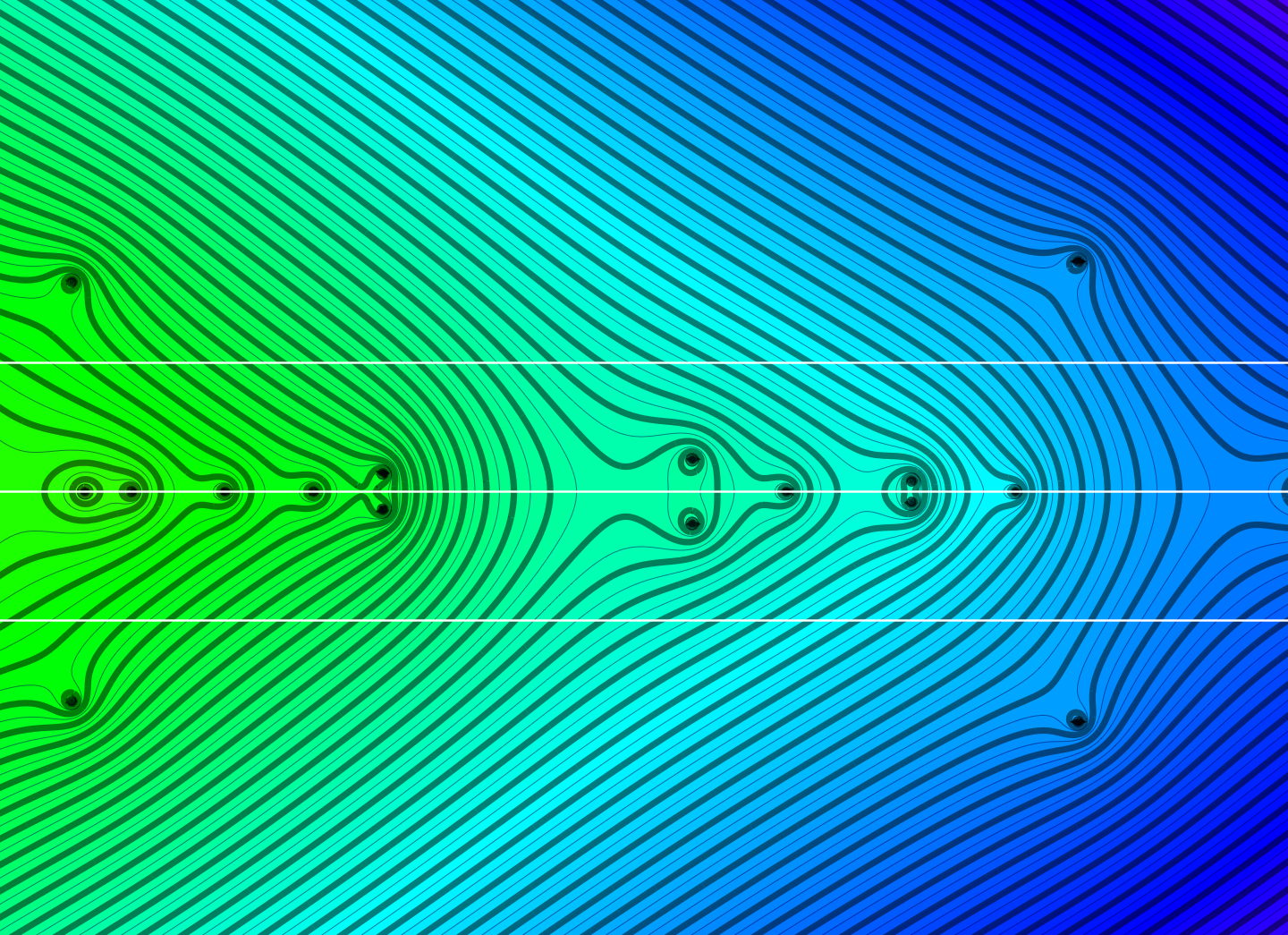
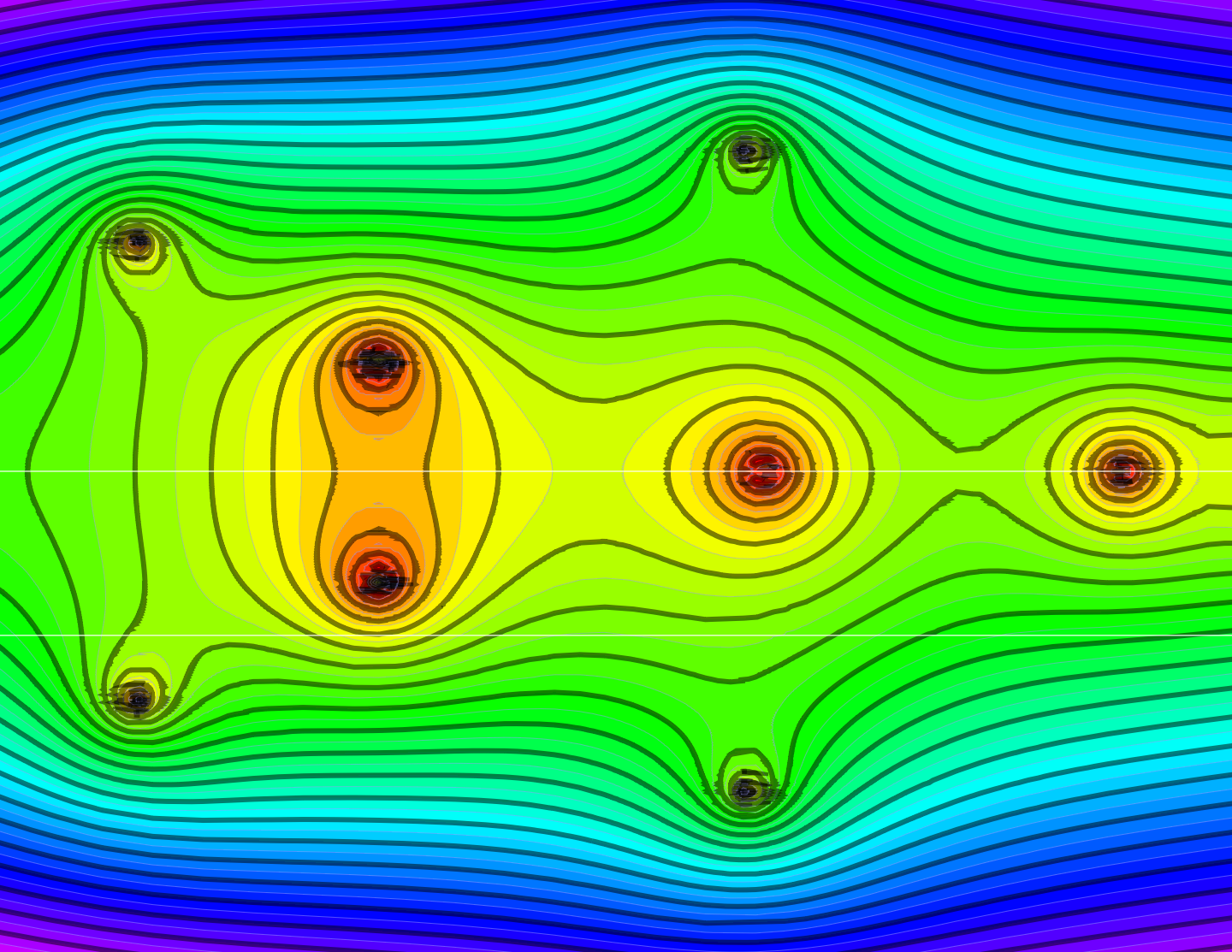
An update on tree and forest indices which measure the exponential growth rate of the number of spanning trees or forests when doing Barycentric refinement. This needs an upper bound estimate of the eigenvalues of the Kirchhoff Laplacian.
Tree Forest Ratio
The tree forest ratio of a finite simple graph is the number of rooted spanning forests divided by the number of rooted spanning trees. By the Kirchhoff matrix tree theorem and the Chebotarev-Shamis matrix forest theorem this is where Det is the pseudo determinant and K the Kirchhoff matrix the …
The counting matrix of a simplicial complex
The counting matrix of a simplicial complex has determinant 1 and is isospectral to its inverse. The sum of the matrix entries of the inverse is the number of elements in the complex.
A Dyadic Riemann hypothesis
When replacing the circle group with the dyadic group of integers, the Riemann zeta function becomes an explicit entire function for which all roots are on the imaginary axes. This is the Dyadic Riemann Hypothesis.