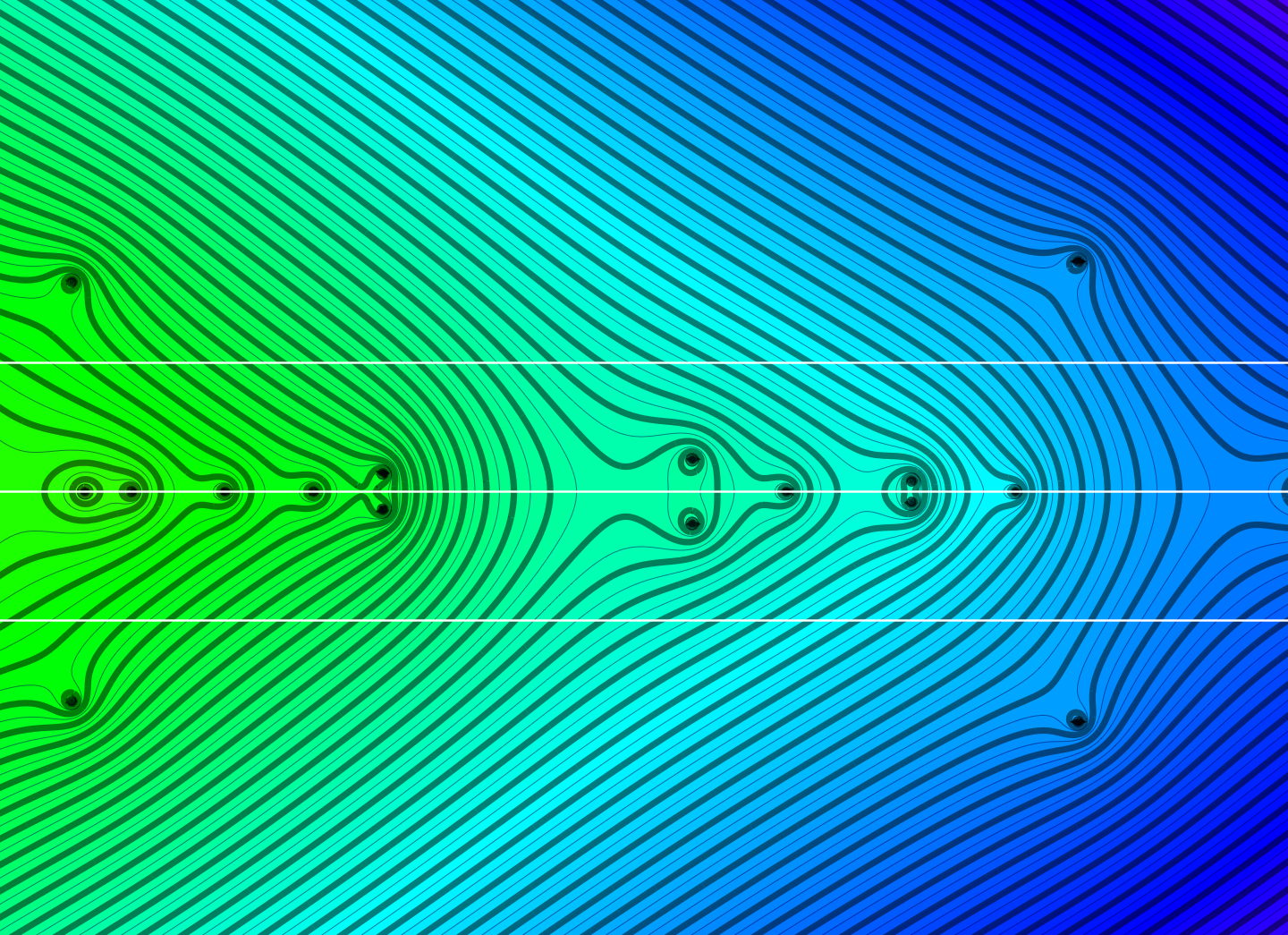
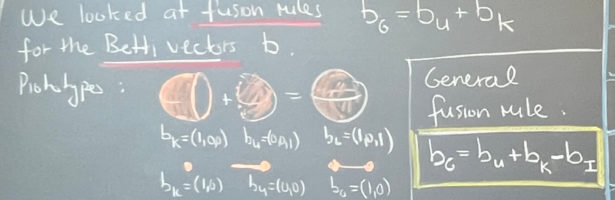Nonlinear Waves
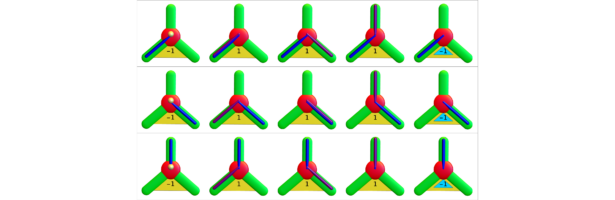
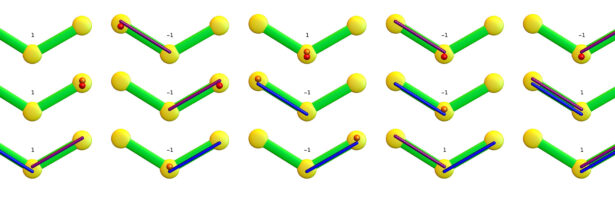
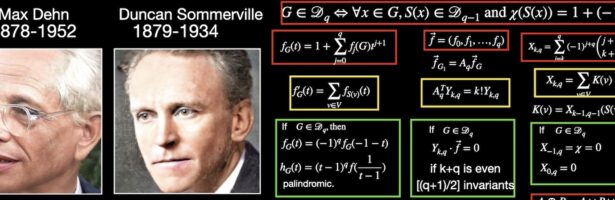
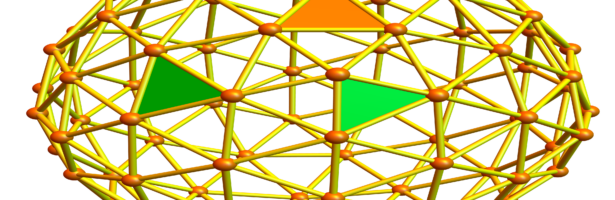
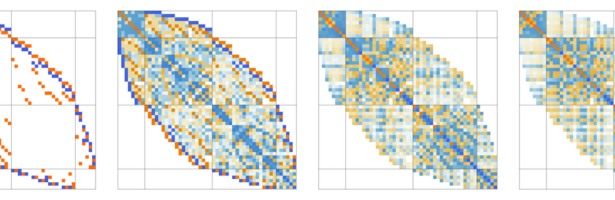
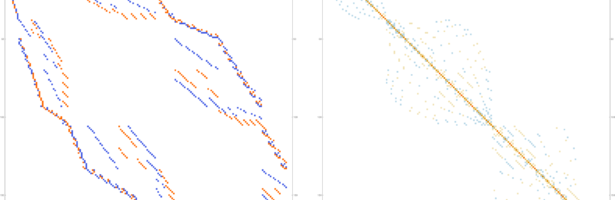
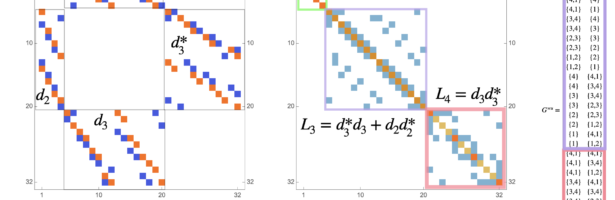
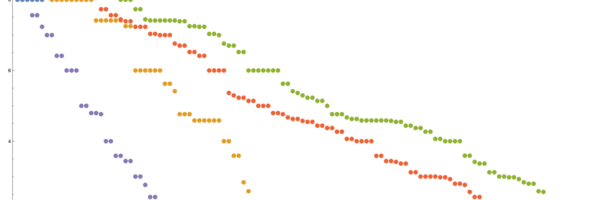
A geometry is a space on which one has a derivative and notion of integration. This can be expressed more elegantly as a space with a cohomology as cohomology are kernels of matrices defined by the derivative and when looking at operators one needs a Hilbert space which intrinsically defines …