In order to construct the geodesic manifold of dimension k in a q-dimensional manifold, we build up the manifold in the discrete Grassmannian bundle Gr(q,k). We now do this all using the geodesic flow, which is much closer to the continuum. The simplex y in x defines (k+1)! geodesics or …
A good discrete differential geometry should mirror the continuum as closely as possible. Positive curvature manifolds should be bounded, the list of positive curvature manifolds should be identical to the ones we know in the continuum. Last year we had looked at geodesic patches and defined sectional curvature by defining …
Given a finite abstract simplicial complex G that is a q-manifold, we consider a k-simplex y in an oriented maximal simplex x as an element in the Grassmannian G(k,q). Of course we are in finite geometry and have no vector spaces but a maximal simplex serves as a q-dimensional frame …
At the end of the wave front calculus paper, I added some pictures about curvature defined by wave fronts. The Bertrand-Diguet-Puiseux formula is remarkable as it shows that one can get curvature of a 2 manifold by measuring the length of wave fronts. Positive curvature means that the wave front …
A first draft is now available [PDF]. The entire topic is a bit off main stream, but that’s why I’m actually quite proud about it, especially because it is not in a field, I’m most familiar with (partial differential equations). It needs courage to work in a new field and …
In our project, we looked at the deformation of exterior derivative df in a q-manifold given by and saw that it satisfies the modified wave equation , where is the Hodge Laplacian. Lets call the left hand side . The equation is a Sturm Liouville problem. Indeed, we can write …
It usually takes a few decades until some mathematical object slides into Pop culture and eventually becomes kitsch. The Black-Scholes differential equation origin from the 1970ies. It is derived from stochastic process model. It became Pop culture in 2000, when NOVA made a TV show about it. It became infamous …
The Polarization identity for quadratic forms like inner products is also known as the parallelogram law. It is very important and always a good teaching moment in a multi-variable calculus course. It is more than just an identity. It tells that if know “lengths”, then we can recover “angles”. All …
In the video below I gave a bit of an overview about the “wave calculus project”. At the 5 minute mark , I mention again the fact that we describe a calculus where distances are quantized but where we still have all the symmetries that exist in the continuum. One …
I only learned recently thought the “not even wrong” blog that Konrad Osterwalder passed away last December. He had been department head at ETHZ from 1986-1990 which overlapped quite a bit with my graduate student time there. He then became rector of ETHZ and became later an important figure in …
The three dimensional space is important because we live in it. With the scalar Laplacian in dimension q=3, the Hydrogen operator (leaving out constants) essentially explains the periodic system of elements and so the starting point of chemistry. The eigenvalue difference explain spectral lines (like Lyman (UV light) , Balmer …
This is a continuation. We look more closely at the 2 dimensional case. The transition from 1 to 2 dimensions is crucial in the context of discretization. In the one dimensional case there is little choice on how to discretize calculus because there is only one possible discretization of the …
We discuss the exterior derivative on a compact Riemannian manifold (M,g) in dimension 1. It is a bounded operator with the property that for a k-form f, the (k+1)-form only depends on f located on the wave front . This notion emerged when searching for a natural multi-variable calculus in …
Here is a bit of calculus in dimension q. I use the letter q and not d for the dimension as we will use the exterior derivative d later. Multivariable calculus is very similar to single variable if one uses multi-index notation like or or or for partial derivatives or …
The dispute of 1689 between Newton and Huygens was won by Newton (he was by far the more important person) but in reality, Newton was wrong (*). With all the information available at that time, the “guess” that light is made of corpuscular objects should not have been tenable at …
If P is a light source on a cube we can look at , the wave front. Every point of this wave front can be assigned a group element, the rotation which is needed to rotate the initial Frenet frame at the start to the frame at time t. Whenever …
This winter, I started to revive some seeds which have been placed in the winter of 2010. It is a calculus in a general compact Riemannian manifold in which the exterior derivative is bounded. It builds on the usual exterior derivative d defined on a manifold (M,g) and builds for …
We currently make some more experiments for the density of wave fronts project. We conjecture there for example that for any polygon wave fronts become dense. In cases like eqilateral triangles or right angle triangles this can be proven because doubling produces a parallelogram that tessellates the plane. This is …
Here is again some Mathematica code. What is new here, that we do not bother to solve the Lax differential equations but directly compute the deformation using QR which is exact. We build a small 3 sphere as a simplicial complex G, then build the Dirac matrix B=D (we chose …
A geometry is a space on which one has a derivative and notion of integration. This can be expressed more elegantly as a space with a cohomology as cohomology are kernels of matrices defined by the derivative and when looking at operators one needs a Hilbert space which intrinsically defines …
Causality Principle One of the most exciting principles in physics is the Huygens principle relating the geodesic motion with the wave dynamics. If we are in a Riemannian manifold, there are two type of “wave fronts”. We can look at the solution of the wave equation , where is the …
This is a bit a blast from the past. While thinking about waves, I thought of this little C program, I wrote in April 2000 (we moved in June 2000 to Boston which was quite an adventure, our car broke down, and I drove from Austin to Arlington twice). As …
For slides and first remarks about the P-NP problem, see this page. I mentioned there my own personal predictions about the Millenium problems. See also this talk from 8 months ago about the perfect number problem in which also all Hilbert, Millenium and Landau problems are mentioned. So, here is …
Having talked a bit about GR (general relativity) and the SM (standard model), lets talk a bit about QM (quantum mechanics). Without any doubt, GR,SM and QM are three extremely successful pillars of modern fundamental physics. Their track record with experiments is monumental (*). We have played with simple games …
In 1960, Regge formulated a discrete calculus as a numerical scheme for relativity. We can formulate it as a theory on a weighted graph . where is a distance which is a discrete q-manifold. The graph defines a q-dimensional pure simplicial complex generated by the maximal complete subgraphs as facets. …
The number theory of quaternion integers has connections to many beautiful parts of mathematics. The quaternions themselves are selected out from all the structures in mathematics as the only associative real non-commutative division algebra and so play a rather unique role in the entire landscape of mathematics. Its unit sphere …
The topic is a combination of the “particles and primes” and geodesics in discrete manifolds” topics, I had worked on before. The first one is an elementary connection between primes in division algebras and particle phenomenology, the second is a completely deterministic dynamical system in combinatorics that has many properties …
AXIOMS: Most basic mathematical structures are heavenly in the sense that they would be discussed in any part of the universe. In algebra these would be groups or rings. In topology these would be topological spaces or metric spaces, in probability theory it would be sigma algebras and stochastic processes. …
We have seen last time that describing many particles moving on a manifold is best done by keeping on each cell a tag telling how many particles there are there. In other words, we do not evolve a sequence of maps but a divisor . This is more effective if …
On October 15, 2025, Sourav Chatterjiee gave the second of the Millenium prize lectures. I have started a page on this here where the slides are included. A bit of nostalgia Some of my own course assistants (when I was an undergrad) or grad student colleagues (when I was a …
This is a bit about getting back to the story of geodesics. See “Geodesics for Discrete Manifolds” and “interacting geodesics on discrete manifolds”, all from earlier this year. I wanted to get next week on how to evolve Gaussian integer and quaternion integer particles. The quaternion primes show a nice …
Manifolds are in the following two dimensional, compact, connected and without boundary. Their classification of these geometric objects is a classical piece of mathematics, completed in a satisfactory way in 1907 by Dehn and Heegaard: the structure is that there are two monoids. The monoid of orientable manifolds that is …
If K(t) is a function in a Lie algebra then the Frenet equations Q'(t)=K(t) Q(t), Q(0)=1 defines a path in the corresponding Lie group. We can now use K(t) to define the Frenet path using the equation R'(t)=Q(t). This defines r(t), where r'(t) is the first row of R(t). The …
The arrow of time is probably one of the most written fundamental topics in physics. I myself have written about it once. To the right are some writings and movies related to time and these are only the movies or books I have seen. My favorite math book pair about …
A periodic Frenet curve in is up to isometry uniquely defined by a periodic curve in where the later describes the motion of the Frenet frame. Differentiation then defines a periodic curve in the Lie algebra . We can now reverse the story and start with a periodic curve in …
Maybe it is a good idea to add current “discovery code” also with the Dirac part. It can be helpful to post code also to be able to see in the future how one was thinking at the time. In the talk of Freedman, there was a slide with a …
Update October 7, 2025: Kitsch is already produced by professional mathematicians . No problem if it is declared as such. I myself like some kitsch. It just has to be declared as fake. It feels a bit like climbing “action direct” with the help of the rope. No problem, if …
Let (G,T) be a finite dynamical system. This means that G is a finite abstract simplicial complex and T is an invertible simplicial map (a permutation of G coming from a permutation of the vertex set V or alternatively, a homeomorphism of the topological space which origins from a permutation …
Yesterday was 9/16/25. You can easily check that it is the only date that is a Pythagorean triple MM/DD/YY. I tweeted And made a brief short on youtube about Elkies’s puzzle explaining visually that . If one is asked about the minimal number of puzzle pieces which can explain this …
Here is my “discovery code” used over the weekend to detect first experimentally that there are dynamical connection and green function matrices which are inverse of each other. I might talk about the proof next time. But first to the experiments. I take here a concrete example of a finite …
In the evening of the 13th of September after giving the talk below, it dawned me after doing lots more experiments that the connection dynamical connection Laplacian and the dynamical connection Green function that were written down on the right hand side of the black board work together if one …
When I had been studying mathematics at ETHZ, taking two semesters of calculus and at the same time taking two semesters of linear algebra had been mandatory. My Calc 1 (1a/1b here) and Calc 2 (21a here) teacher from the first year was Hans Laeuchli. His advisor Ernst Specker during …
When trying to translate everything that has been done in mathematics to the finite world it is good first to look at the most important theorems. Some of the theorems like the pigeon hole principle or the law of the product or the fundamental theorem of arithmetic do not need …
For a finite abstract simplicial complex, we can look at the Dirac Zeta function, the Connection Zeta function and the Lefschetz zeta function. My work on this in the last couple of years
Here is an other “poem” that has been added to the “math poetry page”. Given a simplical complex G, it computes the automorphism group Aut (its group of symmetries, meaning invertible simplicial mapss) and for each T computes both the Lefschetz number and the sum of the indices of the …
During a nice 23 K run on Friday, I was thinking a bit about Lefschetz. This is one of the first stories, I tackled. See the paper. It is one of my 10 favorite theorem in graph theory. I originally formulated it in graph theory in 2012 generalizing the one …
A conference earlier this year had the effect that some main stream media started to report about it. I saw it here in an Austrian journal. But the article does not report on any new discoveries. The 2025 Ultrafinitism Conference was also a cover story for NewScientist Magazine. I thought …
Given a finite abstract simplicial complex G, there are two amazing matrices which are two sides of a coin. Both matrices are symmetric n x n matrices if G has n elements. The Dirac matrix D =d+d* is defined by the exterior derivative d(x,y) = sign(x,y) if y is incident …
Before we start, here is the code which generated the two matrices on the board of the talk. 5 lines for the Hodge Laplacian, 1 line for the Connection Laplacian. This works for any simplicial complex. Not only in physics, also in mathematics, there is a fundamental distinction between Fermionic …
Theorem: if a graph G=(V,E) with n=|V| vertices and m=|E| edges and maximal vertex degree d satisfies , then G satisfies the Brouwer conjecture . This adds confidence that the conjecture is true. As mentioned in the video (and now having worked on it for 3 weeks and wrapping up), …
Let G=(V,E) be a graph with n vertices and m edges. So far all experiments indicate that also the signless Kirchhoff Laplacian |K| =D+A satisfies the Brouwer bound for all $late 1 \leq k \leq n$, where is the sum of the largest eigenvalues of |K| and . The signless …
If K is the Kirchhoff matrix of a finite simple graph with n vertices and m edges and eigenvalues and edge degrees . Define and and and . This is . Then the following general inequalities are known (the first 4 inequalities in the following list) or conjectured (the last …
One of the most amazing formulas in linear algebra is the Hadamard first variation formula which tells how an eigenvalue changes if the matrix entries are changed. Take a symmetric matrix K and perturb it as K+t E, where E is an other symmetric matrix. How do the eigenvalues change? …
John Walker (1949-2024) was an amazing programmer. His website “Fourmilab” was a page of inspiration for me since 1994, when the web started to get serious with Mosaic allowing to brouwse the internet. I still remember in early spring 1994, when I was busy finishing my PhD, that near our …
The elements of Euclid of Byrne (internet archive) are a nice example also in how to illustrate mathematics. The tools to illustrate mathematics have multiplied since Byrne’s time. Yesterday, I wanted to visualize the identity w(B(x))=w(U(x))-w(S(x)) for quadratic (Wu) characteristic which comes after linear (Euler) characteristic. In the video, the …
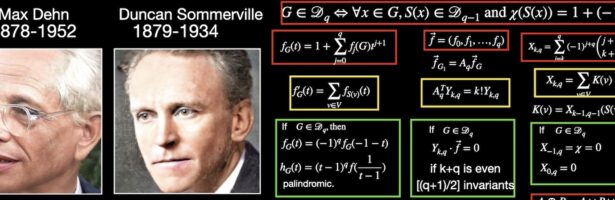
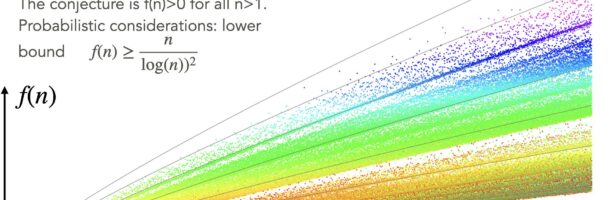
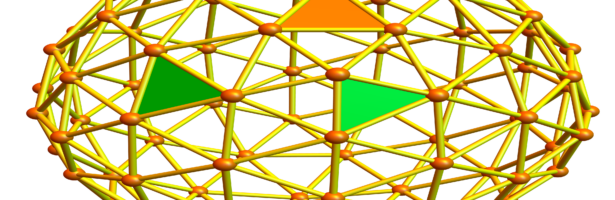
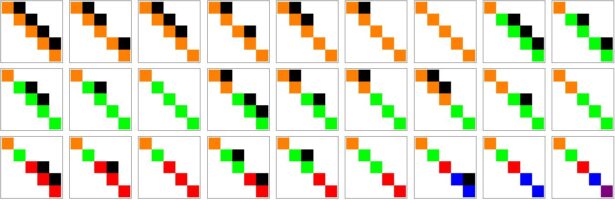
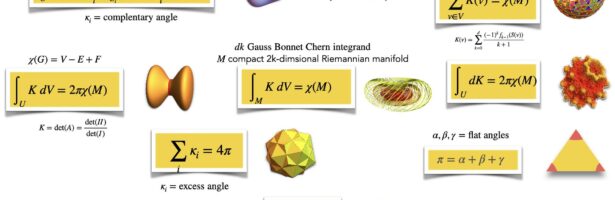
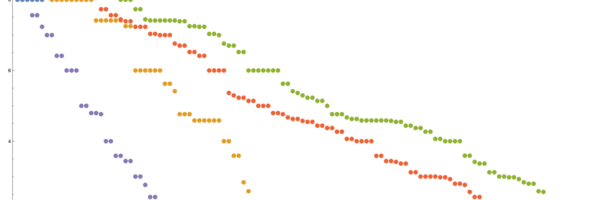
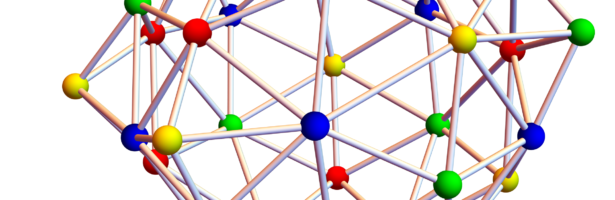
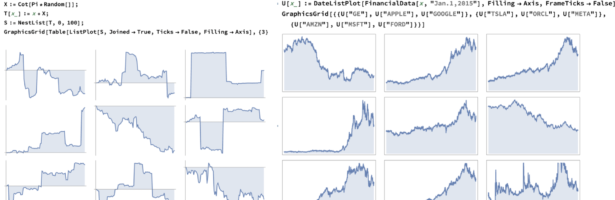
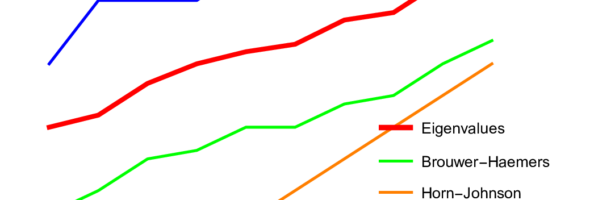
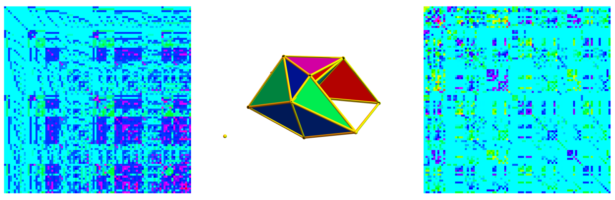
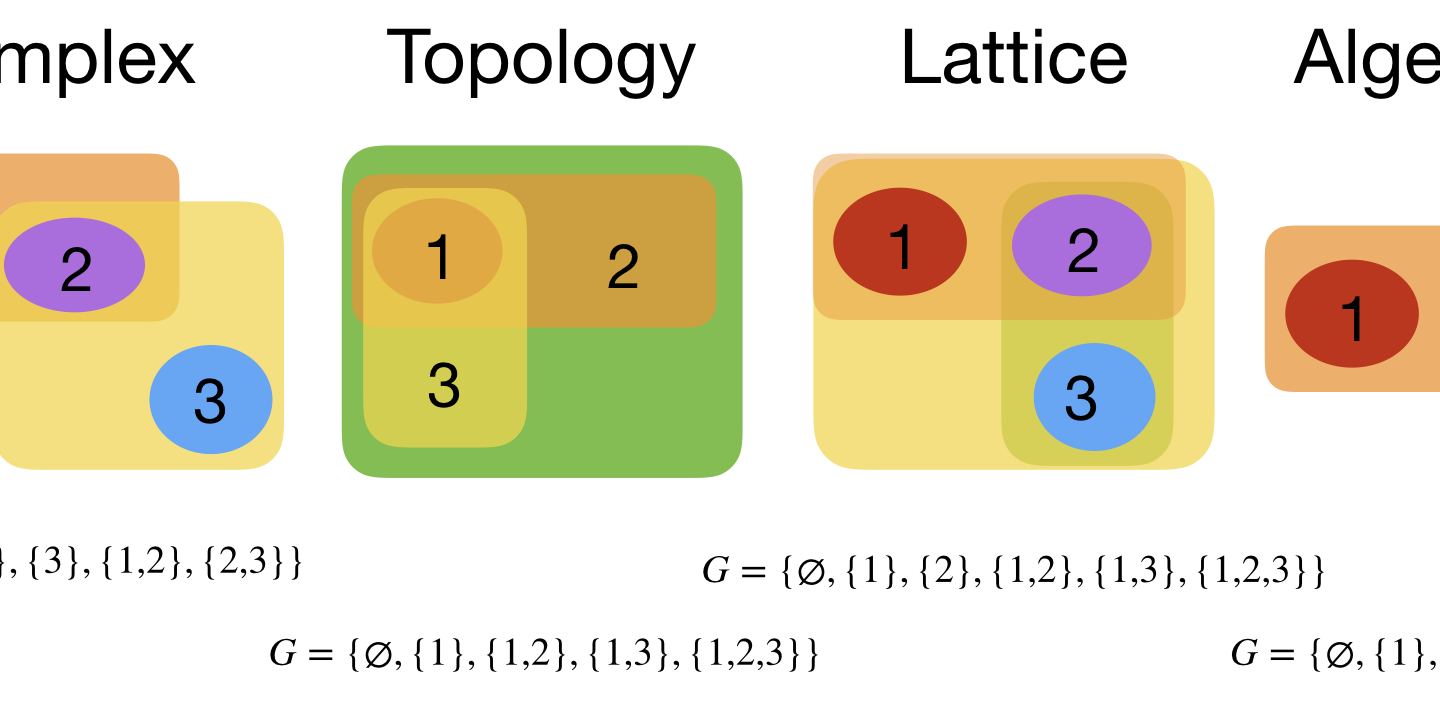
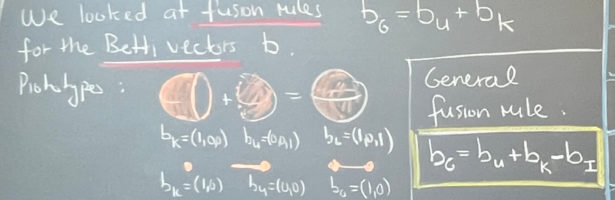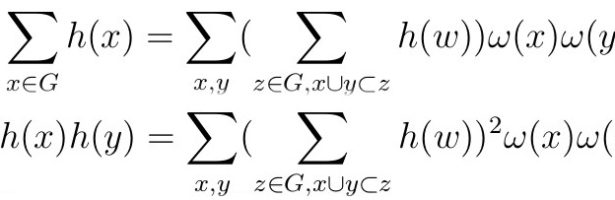While thinking about some fundamental parts in the story of Dehn-Sommerville, I decided to make a bit of an exercise in imagining how Euclid would have done finite geometry. The result is given in the movie below. Euclid’s elements is undoubtedly one of the milestones in the whole of mathematics …
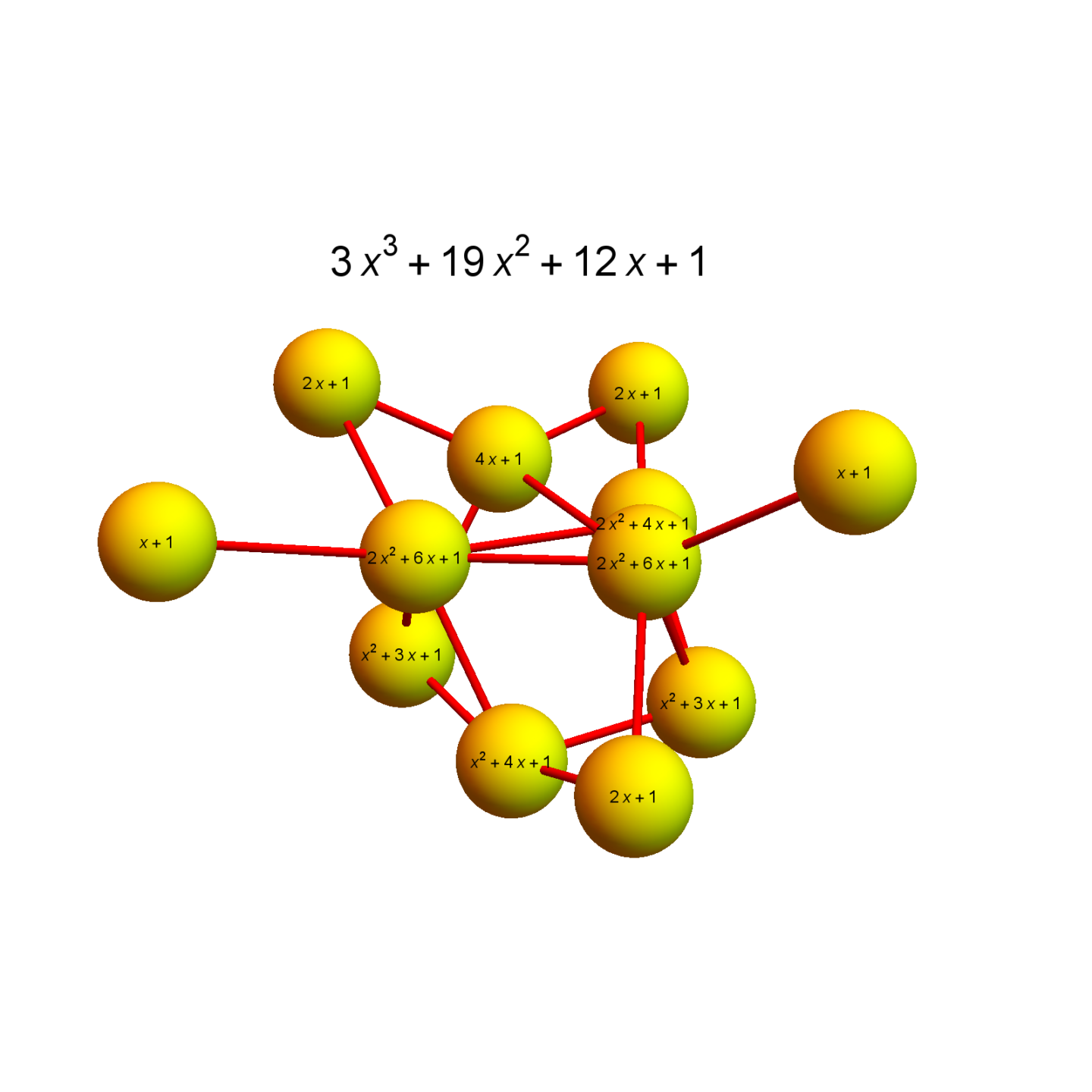
Next week, I will be back in my office. As they are constructing labs just near my temporay office, I made this “talk to myself session” in a seminar room of the department. I try to finish these days a review about Dehn-Sommerville, a rather unpopular topic historically speaking (not …
Goldbach has been hugely popular recently. It appeared in movies, and books. on some major youtube math sites like numberphile or veritasium recently. That show featured also Harald Helfgott, who had shown the ternary conjecture more than a decade ago. The conjecture is probably the most popular math problem of …
Dehn-Sommerville identities are symmetries for manifolds. First detected by Max Dehn in small dimensions, they were generalized by Duncan Sommerville in 1927. The relations were classically studied for simplicial polytopes which means q-spheres. It gives relations for the f-vector of a simplicial complex that is a q-sphere. The original work …
In a recent interview with Lex Freedman, Terrence Tao brought up the allegory of foxes and hedg-hogs in mathematics. Foxes know lots of things, hedgehogs know one thing well. As for a reference, I found this allegory. There are other analogies: Freeman Dyson indicated how Francis Bacon and Rene Descartes …
While walking through the ETH library in Zuerich on Monday, I saw a new book from 2025 by Brian Hopkins called “Hands-On Combinatorics: Building Colorful Trains to Manifest Pascal’s Triangle, Fibonacci Numbers, and Much More”. The ETH library is very nice. I used to work there myself often as a …
Summary We look at 5 results of Peter Lax (1926-2025) in a youtube short (1 minute clip) 1) 1956: Lax Pairs for integrable system2) 1990: Pedal Map in geometry: a chaotic system3) 1971: Approximation theorem of volume preserving continuous maps4) 1954: Lax Milgram theorem generalizing the Riesz representation theorm5) 1956: …
As promised in the talk, here are the 12 lines of code. The 13th line is an example and take the smallest 3 dimensional manifold G, the 16 cell which is a small example of a 3-sphere. The fiber bundle P has 384 elements in this case. Every single particle …
Here is the start of the novel “Schild’s ladder” by Greg Egan from 2004. It has sometimes been called the hardest SciFi Novel. Indeed, you can already be stuck in the first paragraph. The text describes the diamond lattice (there is a Wolfram demonstration file here by Sandor Kabai from …
One of the problems which has bothered me in the last couple of months is the fact that in a locally finite geometry G, it is improbable to get a notion of geodesics which satisfies the properties: 1. any two points can be joined by a geodesics, 2. there is …
After talking about this on Saturday, I tried some other things (this is a perfect topic to think about before getting to sleep or even contemplate about while sleeping). First of all, we can extend how to evolve the geodesic flow given a triangle t=(a,b,c) in a q-simplex x of …
[Update June 17, 2025: The Senior thesis: Spectra and Similarity by Jessie Pitisillides and the preprint on the ArXiv: (Segre Characteristic Equivalence) of Jessie Pitsillides.] Every linear algebra course battles the concept of similarity. We learn that trace, determinant, rank or eigenvalues allow to check whether two matrices are similar …
While teaching probability this semester, I had naturally to think again at the central limit theorem and took this as an opportunity to warm up a bit something I abandoned in 2022 after learning that what I was following has been understood already by mathematicians like Levy or Gnedenko. Still, …
A closed geodesic in a q-manifold is a q-manifold C with boundary dC. This boundary dC is a circle bundle. It can be for example. But it can also be a non-trivial bundle. Note that everything is purely combinatorial and pretty small. For the Moebius strip for example C is …
Given a q-manifold, we have a geodesic dynamics T:P -> P, where P is the oriented frame bundle. Most geodesics are not simple but we can look for the number of simple closed geodesics and so investigate questions close to the Ljusternik-Schnirelmann theme in the classical setup. For any 2 …
One can for discrete billiards ask questions which are classical in the continuum. One of them is Guillemin’s conjugacy problem, which is an inverse problem. It is problem 6 in my personal favorite list of open problems in Hamiltonian dynamics from 25 years ago. This is a problem which in …
[Update March 23: a paper draft is up. The ArXiv version contains also more code.] Spring break is a good time for some programming and cleanup. I reorganized our home office, took everything apart and rewired the half a dozen computers new, got rid of about 30 old harddrives, mostly …
This spring, scientific american was asking around in departments about problems mathematicians are thinking about. I immediately wrote back mentioning the “odd perfect number problem“, a problem which has for strange reasons been snubbed by problem collections. The article in SCIAM has now appeared. As I had once taken the …
Recently, monopoles was mentioned in a youtube episode of Hossenfelder’s show. For, me, it had always been more natural that monopoles do not exist. Let me explain. Electromagnetism is defined if one has a geometry with an exterior derivative d. This is very general and works for delta sets. The …
Riemannian geometry is related to general relativity, probability theory is related to quantum mechanics. Length enters in GR in the form of geodesics, paths of mass points and curvature, the deformation of space through mass. Probability enters in quantum mechanics by seeing solutions of wave or Schrödinger equations in terms …
Shortly after working on Gauss-Bonnet-Chern for graphs, I wrote about Poincare-Hopf for graphs. It took a larger part of the winter break 2011/2012 to come up with the formula where is part of the unit sphere where the function value is smaller than the function value at v. The function …
A discrete 2-manifold [PDF] is a finite simple graph for which all unit spheres have d(v)=4 or more vertices. The smallest example is which is the octahedron graph and where every unit sphere is a circular graph with 4 elements. The Eberhard curvature is very rigid: the Mickey Mouse theorem …
Curvature is a local notion in a finite geometry that adds up to a topological invariant. This is Gauss-Bonnet. I’m only really interested in curvatures that satisfy this exactly. This does not exclude sectional curvature, the latest venture because sectional curvature integrated over a geodesic sheet is the Euler characteristic …
We continue to look at examples of a-manifolds. Besides level sets we can also do connected sum constructions. In the talk, I glue together two manifolds along a q-simplex. An other possibility is to glue along a wall, a (q-1) simplex, removing two simplices attached at a hypersimplex and glue …
We have to adapt the geodesic flow in two situations: for manifolds with boundary or for manifolds obtained as level sets in other manifolds where we want to define the geodesic flow directly in the open set and not first pass to the Barycentric refinement. In both cases, we sort …
We continue the quest to define a sectional curvature for q-manifolds. A good notion should produce classical theorems like that if sufficiently pinched manifolds are spheres. Asking all embedded wheel graphs to have positive curvature was much too rigid and produced only spheres, so small that I called this the …
If G is a q-manifold, we have defined a geodesic dynamics T on the frame bundle P, a principle fiber bundle with structure group . As we have seen last time, the geodesic update step , where is the dual sphere of the -simplex . Everything is finite. G is …
The Shashibo puzzle is a game in the category of geometrically realized simplicial complexes of dimension q=3. One can also play it combinatorially, meaning to disregard geometric realization and just look at finite set of finite sets. One can see it as a playing with 3-dimensional complexes generated by twelve …
Here are two fundamental problems for discrete q-manifolds (a notion which can be defined for the trinity of geometric structures, that is for finite simple graphs as well as for simplicial complexes or delta sets). As for 1, one could ask that every embedded wheel graph has positive curvature. This …
Herbert Groetzsch and Jan Mycielski worked in the 50ies on the chromatology of triangle free graphs. Groetzsch’s 3 color theorem assures that planar triangle free graphs have chromatic number 3 or less. Mycielski defined an operation on graphs which preserves triangle free graphs and increases the chromatic number exactly by …
Coloring manifolds is a wonderful theme because it is not that well studied and so has many low hanging fruits. Here is an other one. For d-manifolds, the chromatic number is between d+1 and 2d+2 and a growth rate (3d+1)/2 is observed and reasonably conjectured upper bound. I started to …
The Regge approach to discrete relativity is also related to graph coloring problems of d-manifolds. While one can look at the length of the dual sphere of a codimension-2 simplex as a notion of curvature, the distinction of whether this circle has even or odd length is relevant when wanting …
The definition of soft Barycentric refinement needed adaptation so that it preserves manifolds with boundary. If G is a finite abstract simplicial complex. The Barycentric refinement is the Whitney complex of the graph in which G are the vertices and where two points are connected, if one is contained in …
A finite abstract simplicial complex G, a finite set of non-empty sets closed under the operation of taking non-empty subsets, has not only a wonderful topology in which the stars form a basis and the cores are closed, but also a hyperbolic structure as the unit sphere is the join …
General relativity plays on a pseudo Riemannian manifold (M,g). The Einstein equations describe how matter defines the space time and the geodesic equations describe how mass moves in space time. It is maybe the most beautiful theories that exist as it describes a relatively complicated frame work as part of …
Gauss-Bonnet tells that integrating curvature K over the geometry G is Euler characteristic X. Curvature K is a quantity attached to points in the geometry and Euler characteristic X is an integer. A consequence of the continuity of the functional getting from K to the integral is continuous, a rigidity …
What is the reason for the structure of the Standard Model? For a mathematician, it better has to be something inevitable. The model is the periodic system of elements is all based on the geometry of the space G one considers. If G has an exterior derivative, one has a …
There are exactly 3 associative real normed division algebras as the Frobenius theorem from 1879 tells. Each of them produce natural Lie groups . Each of them produces natural dense sphere packings . Each of them produces natural rings , the ring of integers, the Eisenstein ring and the ring …
The 2 dimensional plane can be characterized as the only simply-connected two dimensional flat manifold. In the discrete there is a similar uniqueness. The discrete hexagonal plane is the only 2-manifold that is flat and simply connected. Compact flat 2-manifolds like the torus or Klein bottle are not simply connected …
There is a soft Barycentric refinement of graphs or simplicial complexes which can be seen as the usual Barycentric refinement in which the second highest dimensional simplices are collapsed. It is a triangulation of the dual complex. The soft Barycentric refinement of a d-dimensional cross polytop for example is a …
This is just an update on two topics looked over during the summer. In the case of the QR flow and Toda flow equivalence, I have had a hard time finding it due to some strange ways how Mathematica computes the QR composition. You can try yourself: the diagonal entries …
Here is the proof that is solved by with , the QR decomposition. Proof. We show that is solved . From by $Q_t$ with $latex Q’=QB, Q^*=- BQ^*$, we get . Look at the differential equations for Q,R with initial condition . The first equation gives the conjugating orthogonal transformation. …
Update of November 4th 2024: There is a memorial in honor of Henry McKean at NYU on November 15th 2024. Last week, when looking up Henry McKean, I saw that he passed away on April 20, 2024. I don’t recall having met him in person but I have seen some …
A real symmetric matrix is called a Dirac matrix, if it is a block Jacobi matrix in which the side diagonal entries are nilpotent, meaning . For such a matrix, the square is called the Laplacian. It is block diagonal . If is a continuous function such that is invertible, …
A discrete geometry does not have a lot of symmetry as the automorphism group is in general empty. The isospectral set of the Laplacian or Dirac matrix is large enough however. Note that when dealing with a specific class of operators like Dirac matrices, then not all isospectral matrices qualify. …
Since finding the isospectral deformation of the exterior derivative (see “An integrable evolution equation in geometry” from June 1, 2013 and “Isospectral Deformations of the Dirac operator” from June 24, 2013), I tried to find discrete time integrable evolutions of the Dirac operator. Last Sunday, while experimenting in a coffee …
A 2-manifold with boundary is a finite simple graph for which every unit sphere is a circular graph with 4 or more nodes or a path graph with 3 more nodes. The boundary is the set of vertices for which the unit sphere is a path graph, the interior is …
An abstract delta set (G,D,R) is a finite set G with n elements, a selfadjoint Dirac matrix with and a dimension vector defining a partition and Hilbert spaces called the spaces of k-forms. The exterior derivative maps to . The Hodge Laplacian is a block diagonal matrix defining the Hodge …
This is a presentation from Saturday, July 13, 2024. Curvatures are usually located on the zero dimensional part of space. I look here at curvature located on one or two dimensional parts of space. In the special case of a triangulation of a 2-dimensional surface, where the usual curvature is …
Explanations of the Casimir effect using common physics intuition like “polarization” (it originally was studied in the context of van der Waals forces) or “pressure” do not work. The reason in the case of the Casimir effect is that in the case of two planes or two cylinders the Casimir …
In this presentation, there is a bit of advertisement for finite geometry and delta sets in particular. I also tried to get a bit into the history of finitist ideas in geometry and physics(starting with Riemann). One usually thinks about finite projective spaces when talking about “finite geometries”. I like …
I looked at a quadratic cohomology example. For theoretical backgroun, see the ArXiv paper “Fusion inequality for quadratic cohomology”. It is the case when U is a union of two disjoint smallest open sets in a 2-sphere for which I take the Icosahedron, one of the Platonic solids and a …
While linear cohomology deals with functions on simplices, quadratic cohomology deals with functions on pairs of simplices that intersect. Linear cohomology is to Euler characteristic what quadratic cohomology is to Wu characteristic $w(G) = \sum_{x,y, x \cap y \in G} w(x) w(y)$. If the simplicial complex is split into a …
Delta sets are very general. They include simplicial complexes, open sets in simplicial complexes, quotients of simplicial complexes, quivers and so multi-graphs or simply hypergraphs, sets of sets. For the later, the geometry is not that interesting in general. As for quivers, the associated delta set is one dimensional only …
Quivers are graph in which multiple connections and loops are allowed. Since there is a Dirac operator d+d* with exterior derivative for them, they define a one-dimensional delta set (G,D,r), where G is the union of vertices and edges (loops count as edges) and r is the dimension function which …
If is a finite abstract simplicial complex, a finite set of non-empty sets closed under the operation of taking non-empty subsets, we can ask about what f-vectors can occur if counts the number of sets of cardinality k in G. The case of the complete complex with gives a hint …
The smallest open sets in a finite topological space form the atom of space. It was almost 100 years ago, when one has turned away from non-Hausdorff topological spaces and decided they are less relevant (Hausdorff seems have convinced Alexandrov and Hopf to focus on Hausdorff property). This is unfortunate …
Historically, geometry started in Euclidean spaces. There was no concept of coordinate when Euclid wrote the “elements”. Using “points” and “lines” as building blocks and some axioms, the reader there is lead to quantitative concepts like “length”, “angle” or “area” and many propositions and theorem. Only with Descartes, the concept …
Here are three catchy open problems in differential geometry. As with any problem, we can look how to formulate discrete versions. The first problem is whether a positive curvature 2d manifold has positive Euler characteristic, the second is whether there is a positive curvature metric on and the third is …
Finite geometric categories: graphs – simplicial complexes -simplicial sets – delta sets Delta sets were originally called semi-simplicial sets by Samuel Eilenberg and Joseph Zilber in 1950. Similarly than semi-rings are more general than rings or semi-groups are more general than groups, also delta sets are more general than simplicial …
The discrete Sard theorem in the simplest case (which I obtained in 2015) that a function from a discrete d-manifold to {-1,1} has level sets that are (d-1) manifolds or empty. (See here for the latest higher generalization to higher codimension.) A simplicial complex is a d-manifold if every unit …
Here are some links to the articles mentioned in the talk: It surprisingly often happens that a big conjecture tumbles at around the same time. In the case of the Arnold conjecture, several approaches, spear headed by Conley-Zehnder, Eliashberg and Floer have reached the goal. But also almost always with …
The last geometric theorem of Poincare was conceived shortly before the death of Poincare. Poincare had a prostate problem when he was 58 and went to surgery in 1912 which he did not survive. Fortunately his last theorem was sent to an Italian journal two weeks before he died, but …
Finite topological spaces are only interesting if non-Hausdorff. The reason is that every Hausdorff finite topological space is just the boring discrete topology. The topology from a simplicial complex is an example of a nice and interesting topology because it produces the right connectivity and dimension on the complex without …
It is not quite yet a poem, but here, as promised in the movie, some code to generate both the Betti vector and Wu betti vector of a random submanifold in a given manifold. It is 25 lines without any additional libraries, so not yet quite a poem, but it …
My experiments so far indicate that the Wu cohomology of a d-manifold G can be read off from the usual cohomology. If is the Betti vector of G then (0,\dots,0,b_d,b_{d-1},\dots,b_1,b_0)$ appears to be the Wu Betti vector. So far, this is only a conjecture. In the talk, the case , …
[Update 3/5/2024: given that one knows now the optimal Moebius strip, one can wonder about the much easier question of what the smallest simplicial complex producing a cylinder or Moebius strip is. Below, I use in both cases 6 facets (triangles). For the Moebius strip, one can do with 5 …
The video below is an attempt to get back to an older story of Wu characteristic. One of the things which still needs to be explored badly is the Wu cohomology of the complement K of knots H and more generally of the complement K of k-dimensional manifolds H in …
If G is a d-manifold and is an arbitrary map, the discrete Sard theorem tells that is an open set in G that is a (d-k)-manifold. We mean with that the graph encoding the incidence of the sets in H is a (d-k) manifold. The sub-manifold H of K is …
Here is some code illustrating the story. We take the 4 manifold (a favorite manifold of Heinz Hopf) and consider two random functions f,g. Now generate the two manifolds and . They are both 2 manifolds. It goes as follows: the sign data of {f,g} are in which are 4 …
Coordinates are function values. On the two functions and , allow to determine every point in the plane. In the continuum coordinates are commutative: is the same than . This commutativity also holds in Riemannmian manifold settings. In the discrete this is no more true. Lets for simplicity assume we …
The updated document “manifolds from partitions” with more code. I then mention the index theorem for simple graphs dealing with the symmetric index . Writing the unit sphere as a union of and and $M_f(v)$, the center manifold. Now . In the interpretation with the joined center manifold , the …
Again a little bit of a flashback to my earliest steps in doing mathematical research. The Pentagonal number theorem is one of the most beautiful theorems in number theory. It uses the Pentagonal numbers to get a recursion for the partition function . This can be written as ( typo …
In my paper “Manifolds from Partitions”, I stated that that the case of empty graphs can not occur, but did not prove it. It is indeed not true. Here is an update [PDF] with an additional section. It is very rare although that a surjective map produces still an empty …
My experience from my Schweizer Jugend Forscht adventure was not only invaluable from the scientific point of view, I also met some other young aspiring scientists (here is the book with all the participants (PDF)) which was published in 1983 (when I was already a second year ETH student), and …
A nice thing about mathematics is that it has no dogmas, statements which have to be taken on good faith. Axioms come closest, but by nature also, they come with an honest warning that one can either accept them or not. Already Euclid fought with the parallel axiom. Today it …
Brevity contributes both to clarity and simplicity. Surprisingly, it often contributes to generality. I myself am obsessed with brevity. I especially love short code. A short program is like a poem. If it is also effective, it can also be used as building blocks of larger programs. The Unix philosophy …
Eugene Wigner in 1939 associated elementary particles with irreducible representations of groups, especially the Poincare group. In a first year algebra course, we learn about representations of finite groups and especially the symmetric group , where there are p(n) irreducible representations, where p(n) is the number of integer partitions of …
Happy new year 2024. Here is the code displayed on the right upper corner of the board written this morning when wondering how frequent the situation is that the year is divisible by the year modulo 1000 minus 1. This happens for 2024 as it is divisible by 23. The …
First about Sard: (a write-up [PDF] ). I also display a bit my hobbies: Panorama photography (since 1999, a time when panoramas were still stichted). Later with a mirror camera. Then with GoPro Max, Iphone and more recently with the insta 360 camera (I for strange tech enhousiastic reasons pride …
In the program to get rid of any notion of infinity, one necessarily has to demonstrate that very classical and entrenched notions like topics appearing in a contemporary multi-variable calculus course can be replaced and used. Artificial discretisations do not help much in that; they serve as numerical schemes but …
There are lots of finite geometric structures. Graphs are probably the most clear ones. Simplicial complexes can not be beaten in simplicity. And delta sets can not be surpassed by generality. So, they are a geometric incarnation of the paradigm “Simplicity, Clarity and Generality”, which appeared on the book cover …
Here is the table shown in part 2 of the presentation showing some of the toys. It had been generated by Mathematica. It uses manifolds from the manifold page of Frank H. Lutz mentioned in the clip. About the left hand side (of the chalkboard) with some history pointers of …
One of the nice things in mathematics is that one can play with models which do not necessarily have to do directly with the real world, whatever the later means. We can look at abstract objects, like finite simple groups, number theory in some number field or topology in 1001 …
What is {f=0,g=0} for two functions f,g on a graph G. If G is a 4-manifold, these are 2-manifolds or empty.
We look at four different features or properties which can be invoked when looking at a mathematical problem. Why is something beautiful, when is it difficult, how hard is it or are there any surprises?
Arboricity and Chromatic number are linked in various ways. The topic also links to difficult NP complete problems. We muse about how often it is the case that for manifolds the question is easy. An example is the Hamiltonian path problem which is linked to Peg Solitaire
One of the nice things to work in a subject not having grown up in is to be in steep learning curves. I have thought about the arboricity of manifolds for a while now but the fact that the arboricity can be arbitrary large for d-manifolds with d larger than …
We aim to write down a short proof of the statement that a planar graph has arboricity 3 or less.
The Acyclic Chromatic Number is bounded above by the arboricity. We can improve this by one if the Acyclic Chromatic number is even.
We explain why the arboricity of 3 spheres can take values between 4 and 7 and mention that for 3 manifolds the upper bound is 9 (but believed to be 7).
We look at the problem to find the possible arboricities which a 3-sphere can have.
We work on the result that any 2-sphere can be covered by 3 trees.
In other words: three trees suffice.
The three tree theorem tells that any discrete 2-sphere has arboricity exctly 3.
We aim to show that the Lusternik-Schnirelmann category of a graph is bound by the augmented dimension. We can try to prove this by using tree coverings and so look at arboricity.
A notion of a discrete vector should work for theorems like Poincare-Hopf and also produce a dynamics as classically, a vector field F, a smooth section of the tangent bundle on a manifold produces a dynamics . A directed graph does not give a dynamics without telling how to go …
In 1973 Leon Glass proved a discrete Poincare Hopf theorem for directed graphs embedded in a 2 dimensional manifold. Kate Perkins has related this to a discrete Poincare Hopf theorem of mine. This is a discussion of the connection.
This is a bit of a continuation from a previous video about Lusternik-Schnirelmann and Morse. I would like to have this chapter as elegant as possible. As for the video, there is a bit of overlap with a previous video on this from the fall, when I circled back to …
We discuss briefly how to make the cohomology space of a graph into a cohomology ring. In other words, how to define the cup product on the kernel of the Hodge Laplacian.
About the cohomology of measurable sets in a probability space equipped with an automorphism.
The pendulum equation can be solved explicitly using the Weierstrass elliptic function.
Something about knots and something about topological data analysis and something about the general frame work to do mathematics in a finite setting.
A bit the bigger picture about the mathematical and data structures which come in when working on these finite geometries.
A youtube presentation of May 13, 2023. We point out that we have a relatively simple approach to Eilenberg-Steenrod.
It is a simple but interesting fact that if we look at a wave equation with discrete space, we also need discrete time provided we want causality, a property which every wave equation should have. The reason is that the solution equation in a causal locally finite geometry is an …
About the proof of the fusion inequality and the problem of finding the case where the
Dynamical systems on geometric spaces are very common in mathematics. Mean curvature flows, Ricci flows etc. We can think of a subcomplex K in a simplicial complex G as a geometric object. We can not break randomly elements away as would in general lose the property of having a subcomplex. …
We write a bit more about four papers which are relevant for the Fusion inequality on the Betti numbers of an open and closed pair in a simplicial complex.
We prove that the spectrum of the Hodge Laplacian dd* +d*d depends in a monotone way on the simplicial complex.
An update about the scattering problem when an open and closed set merge. During the process the harmonic forms on K and U merge to harmonic forms on G. The open problem is to prove that no new harmonic forms can appear. This is the content of the fusion inequality. b(U) + b(K) – b(G) being non-negative.
Over the weekend, I gave a glimpse on some code which allows to compute the cohomology of an open or closed set in a simplicial complex. Here are 5 lines for cohomology. We see how elegant this can all be. Simplicity, Clarity and Generality. This code could in principle compute …
Over the winter break I started to look at Mayer-Vietoris type rules when looking at cohomology of subsets of a simplicial complex. See January 28, 2023 (Youtube) , and February 4th 2023 (Youtube) and most recently on February 19, 2023 (Youtube). Classically, cohomology is considered for simplicial complexes and especially …
A finite abstraact simplicial complex or a finite simple graph comes with a natural finite topological space. Some quantities like the Euler characteristic or the higher Wu characteristics are all topological invariants. One can also reformulate the Lefschetz fixed point theorem for continuous maps on finite topological spaces.
The Arnold conjecture in symplectic geometry has been tackled with two different approaches. One of them is Morse theory, an other one is Lusternik-Schnirelmann theory.
Even or odd, symmetric or anti-symmetric, integer or half integer, measures or de Rham currents, densities or differential forms, undirected or directed, orientation oblivious, or orientation sensitive, primes of the form 4k+1 or primes of the form 4k-1, permanents or determinants: there are many notions of mathematics which can be …
There were two updates on the Cauchy central limit theorem telling that if the Cauchy mean and risk of a random variable X with PDF f is finite and non-zero, then any IID random process with that distribution has normalized sums which converge in distribution to the Cauchy distribution. There …
There were two triggers for this: first of all the KAM fixed point equation is for c=0 a renormalization map which matters in probability theory, in particular for the Cauchy distribution which is a fixed point under the map which gets from a distribution the distribution of [X+Y]/2, where X,Y …
There are various versions of the implicit function theorem. We look first at the soft implicit function theorem, then a theorem of John Neuberger, then at the twist map theorem which uses a hard implicit function theorem.
Barycentric and Connection graphs Barycentric graphs depend on incidence, connection graphs on intersection. Here are some examples from this blog. Both graphs have as the vertex set the complete subgraphs of the graph. In the connection graph, we take the intersection, in the Barycentric case, we take incidence. Here are …
All data are finite. A computer can only represent finitely many real numbers in an interval. We can connect two such numbers if they are considered equal by the computer. This produces a graph,l the machine graph. It is a special Vietoris-Rips graph. The story can also illustrate non-standard notions.
Leonhard Euler wrote in 1767 a “complete guide to algebra”. It might appear strange that one of the most productive and innovative mathematicians of all time would “waste” his time with writing a textbook for school children. But Euler knew how important algebra is. Not only for school but also …
In the new Netflix documentary “a trip to infinity” the question of quantum space comes up. It is interesting to see Brian Green (the famous TV star covering about quantum gravity, big bang, fabric of the cosmos elegant universe or string theory) now seems have been converted to the “finite …
A bit more about Mandelbulb, Mandelbrot, Hopfbrot and discrete Mandelstuff. Some slides [PDF]. To be pure to the discrete, we also have a short part on Mandelbrot sets in finite rings … Update September 15, 2022: Mandelbulbs in Mathematica in 3 lines. I worked this morning to get this down …
The White-Nylander Mandelbulb is one of the most beautiful objects in mathematics. It extends the Mandelbrot set since one slice is the Mandelbrot set.
We look at two inverse problems in mathematics. The first asks to reconstruct a function from its level curves. The second asks to reconstruct a graph from the quiver spectra.
The current trend in mathematics is to become more and more abstract and strange. We go here the opposite way and look at Riemann-Roch in the simplest possible case, when space is a point!
The video of August 20 also gave a bit of an overview of graph products. I should have mentioned the Lexicographic product (introduced by Hausdorff in 1914) mentioned in my article on Graphs, Groups and Geometry. Here is an abbreviation of the story of that video: for finite simple graphs, …
A new video recorded on August 13, 2022. We look at how Delta sets can be used to define a natural Euler characteristic for quivers. Delta sets have been introduced in 1950 by Samuel Eilenberg and Joseph Zilber. Delta sets are for me much more intuitive than simplicial sets. Look …
About the problem of defining an Euler characteristic for a multi-graph or quiver. While for finite simple graphs we have a natural associated finite abstract simplicial complex, we need for multi-graphs a more general structure. Delta sets do the job and allow to define a good Euler characteristic.
The paper [PDF] on the upper bound is updated a bit. It will also be updated on the ArXiv. In the video below, there is an update. Both for quivers as well as non-magnetic quivers (quivers without multiple connections), we can use induction to prove results. One of the amendments …
Quivers allow to model Schroedinger operators on graphs. With loops we can modify scalar values on vertices, with multiple connections, we can modify the magnetic part. This makes quivers attractive as well as theorems about quivers more interesting. An example was . In the talk last Saturday, I also mentioned …
Quiver Terminology Quivers are finite graphs (V,E) in which also multiple connections or loops are allowed. V is a finite set and E is just a finite set of pairs (a,b) with a,b in V. Now (a,a) loops are allowed as are multiple occurrences of the same entry (a,b). The …
In my theorem telling that the k-th largest eigenvalue for the Kirchhoff Laplacian of a finite simple graph satisfies the bound I use a lemma which generalizes the Andrson-Morley super symmetry result of 1985. That paper had provided a ground breaking upper bound for the spectral radius . The proof …
The definition of soft manifoldss now fixed. It is only fitting to call the old discrete manifolds hard manifolds. Unlike the later, soft manifolds can be multipied. They define a subring of the Shannon ring.
What is space? In Spring 2021, prompted by work on graph complements of circular graphs, I started to think more about discrete manifolds. One can see the definition on this video on discrete homotopy manifolds. In the spring of 2022, the definition got slightly modified and the name homotopy manifold …
An update on tree and forest indices which measure the exponential growth rate of the number of spanning trees or forests when doing Barycentric refinement. This needs an upper bound estimate of the eigenvalues of the Kirchhoff Laplacian.
